 |
Средняя кубическая взвешенная
|
|
|
|
Средние квадратическая и кубическая имеют ограниченное применение в практике статистики. Более используется в статистике средняя квадратическая, но не из самих вариантов x, а из их отклонений от средней 
при расчете показателей вариации.
Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. Это мода и медиана.
Мода (Мо) – значение признака, наиболее часто встречающееся в совокупности, т.е. варианта, имеющая наибольшую частоту.
Например, имеются следующие данные по бригаде:
| Выработка деталей за смену одним рабочим, шт. | Число рабочих |
| Итого |
В данном случае модальное значение выработки равно 20 деталей, т.к. ему соответствует наибольшая частота f = 5.
В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:
, где
х Мо – нижняя граница модального интервала
i Мо – величина модального интервала
f Мо – частота модального интервала
f Мо-1 – частота интервала, стоящего перед модальным
f Мо+1 – частота интервала, следующего за модальным
Модальный интервал – это интервал, которому соответствует наибольшая частота f.
Например, имеются данные по предприятиям региона:
| Группы предприятий по стоимости основных фондов, млн. руб | Число предприятий |
| 14-16 | |
| 16-18 | |
| 18-20 | |
| 20-22 | |
| 22-24 | |
| Итого |
Модальным значением стоимости основных фондов предприятий региона является стоимость равная 18,8 млн. руб.
Медиана (Ме) – это варианта, находящаяся в середине ранжированного вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части – со значениями признака меньше медианы и со значениями признака больше медианы.
|
|
|
Если вариационный дискретный ряд нечетный, то номер медианы вычисляется по формуле:
, где n – число членов ряда.
Например, имеются данные по бригаде:
| Табельный № рабочего | Выработка за месяц, тыс. руб |
Ранжируем выработку по возрастанию признака:
| № по ранжиру | |||||||
| Выработка, тыс. руб. |
Определяем номер медианового показателя 
, таким образом, медиана равна 690 тыс. руб., т.е. одна половина рабочих бригады имела выработку менее 690 тыс. руб., а другая – более 690 тыс. руб.
В случае четного вариационного дискретного ряда медиана равна средней из двух вариантов, находящихся в середине ряда.
Например, имеется заработная плата по 8 рабочим завода:
| Табельный номер | Зарплата, тыс. руб. |
| 5,3 | |
| 4,8 | |
| 5,2 | |
| 5,0 | |
| 5,5 | |
| 6,0 | |
| 4,9 | |
| 5,5 |
Проранжируем ряд по возрастанию зарплаты:
| Номер по ранжиру | Зарплата, тыс. руб. |
| 4,8 | |
| 4,9 | |
| 5,0 | |
| 5,2 | |
| 5,3 | |
| 5,5 | |
| 5,5 | |
| 6,0 |
В середине стоят 4 и 5 рабочие по ранжиру, значит 
Медианная зарплата равна 5,25 тыс. руб.
В интервальных рядах распределения медианное значение (поскольку оно делит совокупность на две равные по численности части) оказывается в каком-то из интервалов. Этот интервал характерен тем, что его кумулятивная частота (накопленная сумма частот) равна или превышает полусумму всех частот ряда. Значение медианы вычисляется по формуле:
, где
х Ме – нижняя граница медианного интервала
i Ме – медианный интервал
- полусумма всех частот ряда
S Ме – сумма частот интервалов, стоящих перед медианным
fМе – частота медианного интервала
Например, имеются данные по предприятиям региона:
|
|
|
| Группы предприятий по стоимости основных фондов, млн. руб. | Число предприятий |
| 14-16 | |
| 16-18 | |
| 18-20 | |
| 20-22 | |
| 22-24 | |
| Итого |
Прежде всего найдем медианный интервал, 
, т.е. медианное значение будет средним из значений у 12-го и 13-го предприятий в ранжированном ряду. Очевидно, что эти предприятия находятся в третьем интервале (18-20 млн. руб.), поскольку его кумулятивная частота равна 18(2+6+10), что превышает половину суммы всех частот ().
Из 25 предприятий региона 12 предприятий имеют стоимость основных фондов менее 18 млн. руб., а 12 предприятий – более 18 млн. руб.
Показатели вариации
Вариация – это различие в значениях какого – либо признака у разных единиц данной совокупности в один и тот же период или момент времени.
Например работники СХПК различаются по доходам, затратам времени на работу, росту, весу, образованию, профессии и т.д.
Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строение совокупности, не показывает, как располагаются около нее варианты осредняемого признака. Чем больше варианты отдельных единиц совокупности различаются между собой, тем больше они отличаются от своей средней, и наоборот, - чем меньше варианты отличаются друг от друга, тем меньше они отличаются от средней, которая в таком случае будет более реально представлять всю совокупность. Поэтому возникает необходимость измерять вариацию признака в совокупностях с помощью ряда обобщающих показателей. К ним относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, коэффициент вариации.
Размах вариации R – разность между максимальным и минимальным значениями признака
R = Xmax - Xmin
Однако размах вариации показывает лишь крайние отклонения признака и не отражает отклонений всех вариант в ряду. Для более точного анализа вариации необходимы показатели, которые отражают все колебания варьирующего признака и дают обобщенную характеристику. Простейший из показателей такого типа – среднее линейное отклонение 
. Оно определяется как среднее арифметическое из отклонений индивидуальных значений от средней без учета знака этих отклонений.
|
|
|
или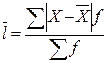 
Среднее линейное отклонение как меру вариации признака применяют в статистической практике в тех случаях, когда суммирование показателей без учета знаков имеет экономический смысл (например, анализ состава работающих, ритмичность производства, оборот внешней торговли).
Дисперсия 
в зависимости от исходных данных вычисляется по формулам простой и взвешенной.
или 
Дисперсия представляет собой средний квадрат отклонений вариантов от их средней величины.
Среднее квадратическое отклонение 
равно корню квадратному из дисперсии. Оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения. Среднее квадратическое отклонение является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты.
Чем меньше значение дисперсии и среднего квадратического отклонения, тем качественно однороднее совокупность и тем более типичной будет средняя величина.
Для сравнения вариаций различных признаков, а также колеблемости одного и того же признака в нескольких совокупностях используют относительный показатель вариации – коэффициент вариации V.
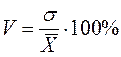
Коэффициент вариации характеризует, на сколько процентов в среднем отклоняются индивидуальные показатели от их среднего значения.
Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.
Например, имеются данные о сменной выработке рабочих бригады, которые представлены интервальным рядов распределения:
| Группы рабочих по сменной выработке изделий, шт. | Число рабо- чих f | Середина интервала x | Расчетные значения | |||
| X f | 
| 
| 
| |||
| 170-190 | -36 | |||||
| 190-210 | -16 | |||||
| 210-230 | ||||||
| 230-250 | ||||||
| Итого | X | X | X |
Исчислим среднюю выработку на одного работника:
(шт.)
Среднеквадратическое отклонение:
|
|
|
(шт.)
Коэффициент вариации:
Таким образом, индивидуальные выработки рабочих за смену колеблются вокруг средней выработки в среднем на 216 изделий или 8%. Данная бригада рабочих по выработке достаточно однородна, поскольку вариация признака составляет лишь 8%, что меньше 33%.
Вариация признака обусловлена различными факторами. Определить их влияние на колеблемость индивидуальных значений признака можно при помощи трех видов дисперсий:
1) общей дисперсии 
2) межгрупповой дисперсии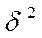 
3) средней из внутригрупповых дисперсий
Общая дисперсия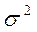 
измеряет вариацию признакапо всейсовокупности под влиянием всех факторов, обусловивших эту вариацию. Она может быть вычислена по простой или взвешенной формуле:
или 
Межгрупповая дисперсия 
характеризует систематическую вариацию результативного признака, обусловленную влиянием факторного признака, положенного в основу группировки.
,т.е. она равна среднему квадрату отклонений групповых средних 
от общей средней по всей совокупности 
.
Внутригрупповая дисперсия 
отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от группировочного признака. Она исчисляется внутри каждой группы:
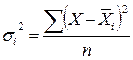или 
На основании внутригрупповых дисперсий вычисляют среднюю из внутригрупповых дисперсий:
Согласно правилу сложения дисперсий общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий, т.е.
Например, при изучении влияния квалификации (тарифного разряда) рабочих на уровень производительности труда в цехе были получены данные, представленные в таблице:
| NN п/п | Рабочие 4-го разряда | N п/п | Рабочие 5-го разряда | ||||
Выработка, шт.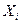 
| 
| 
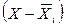
| Выработка, шт.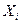
| 
| 
| ||
| -3 | -1 | ||||||
| -1 | -1 | ||||||
| -1 | |||||||
| -2 | |||||||
| Итог | X | X |
Результативный признак – выработка рабочего – варьирует под влиянием факторного признака (квалификации), а также под влиянием других неучтенных случайных факторных признаков. Задача заключается в измерении этих вариаций с помощью дисперсий: общей, межгрупповой и внутригрупповых.
1. Для расчета групповых дисперсий исчислим средние выработки по каждой группе и общую среднюю выработку, шт.:
по первой группе 
по второй группе 
в целом по десяти рабочим 
2.Исчислим общую дисперсию по формуле
Общая дисперсия отражает суммарное влияние всех возможных факторов на общую вариацию выработки изделий в среднем рабочими цеха.
|
|
|
3. Исчислим межгрупповую дисперсию
Межгрупповая дисперсия характеризует вариацию групповых средних, обусловленную различиями групп рабочих по квалификационному разряду.
4. Данные для расчета внутригрупповых дисперсий представлены в таблице.
Внутригрупповые дисперсии
- по первой группе 
- по второй группе 
Средняя из внутригрупповых дисперсий:
отражает вариацию выработки, обусловленную всеми факторами, кроме квалификации рабочих.
5. Проверим правило сложения дисперсий:
Очевидно, чем больше доля межгрупповой дисперсии в общей, тем сильнее влияние группировочного признака (квалификационного разряда) на результативный признак (количество изделий на рабочего).
Для определения этой доли используется эмпирический коэффициент детерминации 
показывает долю вариации результативного признака под влиянием факторного признака.
или 66,6%
Это означает, что на 66,6% вариация производительности труда рабочих обусловлена различиями в их квалификации и на 33,4% (100% - 66,6% = 33,4%) – влиянием прочих факторов.
|
|
|
