 |
Кинематический анализ механизма
|
|
|
|
Исходные данные:  OA= 0,028 м,
OA= 0,028 м,  AB= 0,11 м,w1 = 80 с-1.
AB= 0,11 м,w1 = 80 с-1.
При кинематическом анализе решаются три задачи:
- задача о положениях;
- задача о скоростях;
- задача об ускорениях.
Задача о положениях
Проектирование кривошипно-ползунного механизма. Найдем крайние положения механизма: начало и конец рабочего хода выходного звена. Начало рабочего хода найдем по формуле:
S'= 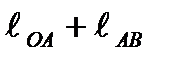 = 0,028+0,11 = 0,138
= 0,028+0,11 = 0,138
где
 - длина кривошипа ОА
- длина кривошипа ОА
 - длина шатуна АВ
- длина шатуна АВ
Конец рабочего хода выходного звена найдем по формуле:
S"=  = 0,11-0,028 = 0,082
= 0,11-0,028 = 0,082
Рабочий ход
S=S' - S"=2r=0,11-0,082=0,028 [м].
Построим механизм в масштабе
m  =
=  ОА / OA=
ОА / OA=  = 0,00056 [м/мм],
= 0,00056 [м/мм],
где ОА – длина звена на чертеже,
m  - масштабный коэффициент длины звена.
- масштабный коэффициент длины звена.
Найдем длину звена АВ на чертеже
АВ =  AB/m
AB/m  =
=  =196 [мм].
=196 [мм].
Покажем перемещение точек в двенадцати положениях механизма. Для этого разделим окружность на 12 равных частей, используя метод засечек. Определим положения звеньев механизма.
Построим шатунную кривую. Для этого найдем центр тяжести каждого звена и соединим плавной линией.
Планы положений механизма используются для определения скоростей и ускорений в заданных положениях.
Задача о скоростях
Кинематический анализ выполняется графоаналитическим методом, который отражает наглядность изменения скоростей и обеспечивает достаточную точность. Скорость ведущего звена:
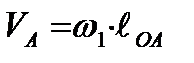 = 80·0,028 = 2,24 [мс-1].
= 80·0,028 = 2,24 [мс-1].
Запишем векторные уравнения:
VB = VA+VВА; VB = VВ+VBВ0,
где VВ0 = 0; VA ^ OA; VВА ^ AB; VB = VBВ0 || оси движения выходного звена.
Величины векторов VBA, VB, VS2 определим построением. Выберем масштабный коэффициент плана скоростей:
 =
= 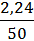 = 0,0448 [мс-1/мм],
= 0,0448 [мс-1/мм],
где pa - отрезок, характеризующий величину скорости на чертеже (мм). От произвольной точки р - полюса плана скоростей отложим вектор ра, перпендикулярный ОA. Через т. «а» проводим перпендикулярно звену АВ вектор АВ. Точка пересечения оси (выбранной в направлений движения) с этим вектором даст т. «в», соединив т. «в» с полюсом получим вектор скорости т. «в». Определим величину скорости т. «в»:
|
|
|
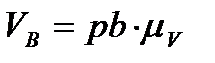 = 25·0,0448 = 1,12 [мс-1].
= 25·0,0448 = 1,12 [мс-1].
Положение т. S2 на плане скоростей определим из пропорции:

Соединив т. S2 с полюсом р, получим величину и направление скорости т. S2:
 = 42,9·0,0448 = 1,92 [мс-1]
= 42,9·0,0448 = 1,92 [мс-1]
Определяем:
 = 45·0,0448 = 2,02 [мс-1]
= 45·0,0448 = 2,02 [мс-1]
 = 25·0,0448 = 1,12 [мс-1]
= 25·0,0448 = 1,12 [мс-1]
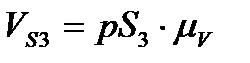 = 20·0,0448 = 0,89 [мс-1]
= 20·0,0448 = 0,89 [мс-1]
Определяем:
 =
=  20,2 [с-1]
20,2 [с-1]
Направление w2 определяется переносом вектора vba в т.В относительно т.А.
| Пара-метр | Положение механизма | |||||||||||
| VBA мс-1 | 2,02 | - | - | - | - | - | - | - | - | - | - | - |
| Vв МС-1 | -1,6 | -2,63 | -2,70 | -2,05 | -1,06 | 1,06 | 2,05 | 2,70 | 2,63 | 1,64 | ||
| Vs1 мс-1 | 1,12 | 1,12 | 1,12 | 1,12 | 1,12 | 1,12 | 1,12 | 1,12 | 1,12 | 1,12 | 1,12 | 1,12 |
| VS2 мс-1 | 1,22 | 1,62 | 2,14 | 2,24 | 1,92 | 1,46 | 1,22 | 1,46 | 1,92 | 2,24 | 2,14 | 1,62 |
| Vs3 мс-1 | -1,37 | -2,19 | -2,24 | -1,69 | -0,87 | 0,87 | 1,69 | 2,24 | 2,19 | 1,37 | ||
| w2 с-1 | -20,36 | -17,78 | -10,44 | 10,44 | 17,78 | 20,36 | 17,78 | 10,44 | -10,44 | -17,78 | ||
Годограф скоростей
Годограф скоростей - это геометрическое место векторов скорости t.S2, в двенадцати положениях механизма приведем к одной точке и соединим их вершины плавной линией вектора скоростей центра масс звена.
Задача об ускорениях
Исследование механизма начинаем со входного звена, определяем ускорение точки А:


 , т.к.
, т.к. 

 = 802 ·0,028 = 179,2 мс-2.
= 802 ·0,028 = 179,2 мс-2.
|
|
|
Определяем масштабный коэффициент плана ускорений
 =
=  = 3,58
= 3,58 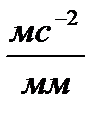 ,
,
где p1a – вектор, характеризующий величину ускорения аA на плане ускорений.
Переходим к исследованию группы 222. Запишем векторные уравнения: 
где aА – ускорение входного звена;
аnВА- нормальная составляющая относительного ускорения звена АВ, вектор этого ускорения на плане ускорений направлен параллельно звену АВ, к точке В.
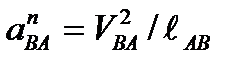 =
=  = 37,09 [мс-2];
= 37,09 [мс-2];
аtВА – тангенциальная составляющая относительного ускорения звена АВ, вектор этого ускорения направлен перпендикулярно звену АВ.
Построим план ускорений. Из произвольной точки P1 - полюса откладываем вектора скоростей aа и anBA. Из конца вектора аnBA проводим вектор аτBA перпендикулярный предыдущему вектору, до пересечения с осью движения звена, совершающего поступательное движение, по которой направлен вектор ускорения ав.
Определим ускорение aAB, соединив на плане ускорений точку а с точкой b. Вектора ускорений центров масс звеньев определяем используя теорему подобия.
Определим величины ускорений, замерив вектора на плане ускорений:
 = 30·3,58 = 107,4 [мс-2] = 0,1074
= 30·3,58 = 107,4 [мс-2] = 0,1074
 = 32·3,58 = 114,56 [мс-2] = 0,1145
= 32·3,58 = 114,56 [мс-2] = 0,1145
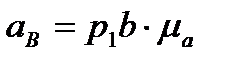 = 58·3,58 = 207,6 [мс-2] = 0,2076
= 58·3,58 = 207,6 [мс-2] = 0,2076
 = 30·3,58 = 107,4 [мс-2] = 0,1074
= 30·3,58 = 107,4 [мс-2] = 0,1074
 = 58·3,58 = 207,6 [мс-2] = 0,2076
= 58·3,58 = 207,6 [мс-2] = 0,2076
 = 63·3,58 = 225,5 [мс-2] = 0,2255
= 63·3,58 = 225,5 [мс-2] = 0,2255
Определим угловое ускорение звена АВ, ε2 = 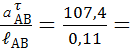 976 с-1
976 с-1
| Параметр | Положение механизма |
 , мс-2 , мс-2
| 0,1074 |
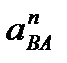 , мс-2 , мс-2
| 0,1145 |
| an, мм | |
| a ва, мс-2 | 0,11456 |
| a в, мс-2 | 0,2076 |
| a s11, мс-2 | 0,1074 |
| a s2, мс-2 | 0,2076 |
| a s3, мс-2 | 0,2255 |
| ε2,с-2 |
|
|
|


