 |
Задание 6. Импульсная и переходная характеристика.
|
|
|
|
КУРСОВАЯ РАБОТА №1
по дисциплине: «Теория информации и сигналов»
ИССЛЕДОВАНИЕ СПЕКТРОВ ПЕРИОДИЧЕСКИХ СИГНАЛОВ
Вариант 6
| Выполнил: студент группы 3300 | __________________ подпись, дата | А.А.Данильчик |
| Проверил: ассистент | __________________ подпись, дата | М.М. Шилин |
2016 г.
Coдержание
Задание к курсовой работе......................................................................................................... 3
Задание 1.Определение спектральной плотности, амплитудного и фазового спектров видеоимпульса 4
Задание 2.Автокорреляционная функция................................................................................ 6
Задание 3.Гармонический анализ периодической последовательности видеоимпульсов 8
Задание 5.Характеристики линейной цепи........................................................................... 10
Задание 6.Импульсная и переходная характеристика.......................................................... 13
Задание 7.Определение токов и напряжений........................................................................ 15
Вывод......................................................................................................................................... 21..........
Литература................................................................................................................................. 22

Задание 1. Определение спектральной плотности, амплитудного и фазового спектров видеоимпульса.
Перед тем как начать анализ сигнала необходимо записать аналитически заданный сигнал (рис.1)

Где 𝚫=0,002 с, Е=1.
Спектральная плотность S(w) равна сумме коэффициентов A(w) и В(w). Так как функция задана двумя выражениями, то эти коэффициенты в свою очередь состоят из A1(w), A2(w), B1(w) и B2(w).

|

|

|

|



Амплитудный спектр равен модулю спектральной плотности или корню квадратному из суммы квадратов коэффициентов А(ɷ) и В(ɷ). Его график представлен на рис.3.
|
|
|

|

|
Рис.3 Амплитудный спектр.
Фазовый спектр определяется как арктангенс отношения коэффициента В(w) к коэффициенту A(w) и он представлен на рис.4.


|
Рис.4 Фазовый спектр.
Задание 2. Автокорреляционная функция
Автокорреляционная функция - временная характеристика сигнала, отражающая связь исходного сигнала и его копии, смещенной во времени.
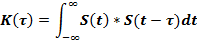
Для нахождения автокорреляционной функции потребуется рассмотреть два варианта величины временной задержки:
1. На рисунке 5 изображен сигнал и его копия, сдвинутая во времени при 0<τ<𝚫.

|
Рис.5. График исходного сигнала и его копия, сдвинутая во времени при 0<τ<𝚫.

|
2. На рисунке 6 изображен сигнал и его копия, сдвинутая во времени при 𝚫<τ<2𝚫.

|
Рис.6 График исходного сигнала и его копия, сдвинутая во времени при 𝚫<τ<2𝚫.

|
Результирующая автокорреляционная функция, представленная на рисунке 7, состоит из двух компонент и имеет вид:
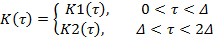

|
Рис.7 Автокорреляционная функция
Задание 3. Гармонический анализ периодической последовательности видеоимпульсов.
Скважность(Q) -это отношение периода (Т) сигнала к его длительности(τ).
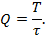
Так по условию задачи дано что Q=4, а длительность сигнала τ=2*𝚫, то Т=8*𝚫=0,016 с.
Зная период можно задать периодическую функцию и построить ее график.

|

|
Рис.8 Периодическая последовательность видеоимпульсов.
Чтобы определить амплитудный и фазовый спектр периодического сигнала используем формулы, измененные для периодического сигнала.

|

|

|
Амплитудный спектр периодического сигнала представлен на рис.9.

|
Рис.9 Амплитудный спектр периодического сигнала.
|
|
|

|
Фазовый спектр периодического сигнала можно увидеть на рис.10.

|
Рис.10 Фазовый спектр периодического сигнала.
Задание 5. Характеристики линейной цепи.
Для определения частотных характеристик пользуются понятием коэффициента передачи или передаточной функции.
Коэффициент передачи равен отношению амплитуды гармонического сигнала на выходе цепи к амплитуде сигнала на входе цепи.

Зависимость модуля коэффициента передачи, равного отношению амплитуд выходного и входного напряжений, от частоты называется амплитудно- частотной характеристикой цепи.
Зависимость аргумента коэффициента передачи от частоты, характеризующая разность фаз выходного и входного напряжений, называется фазово- частотной характеристикой цепи.
Рис. 11 Схема линейной цепи.
Запишем систему уравнений для всех контуров:

|

|

|
Решив систему уравнений найдем ток I1:

|
Подставим его в выражение для Uvx, получим:

|
Запишем выражение для коэффициента передачи:

|
Подставим в выражение полученные выражения Uvx и Uvix, получим:

|
Для упрощения выражения выразим сопротивления R3, R2 через сопротивление R1и коэффициент a. Индуктивность L2 выразим через L1 и коэффициент b, и постоянную цепи:

|

|

|

|
После подстановки и упрощения получим:

|
Рассчитаем коэффициенты:

|

|

|
Получаем:

|
Для удобства умножим полученное выражение на 20:

|
Вычислим амплитудно-частотную характеристику:

|
Вычислим фазочастотную характеристику:

|
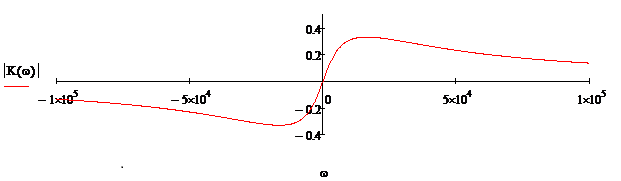
|
Рис.12 Амплитудно-частотная характеристика.

|
Рис.13 Фазочастотная характеристика.
Задание 6. Импульсная и переходная характеристика.
Переходной характеристикой h(t) называется реакция цепи на входное воздействие в виде единичной функции.
Импульсной характеристикой g(t) называется отклик системы на минимальное по длительности, но бесконечно большое по амплитуде, воздействие.
Определим переходную характеристику цепи операторным методом. Запишем коэффициент передачи в операторной форме.
|
|
|

|
Для нахождения переходной и импульсной характеристики используем теорему вычитов.
Переходная характеристика определяется выражением
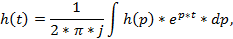

|

|
Выделим числитель и знаменатель:

|

|
Найдем корни:

|
Вычислим:

|
Вычислим переходную характеристику:

|
График h(t) представлен на рис.14
Рассчитаем импульсную характеристику:

|
График импульсной характеристики представлен на рис.15

|
Рис.14 Переходная характеристика

|
Рис.15 Импульсная характеристика
|
|
|


