 |
Точечные оценки неизвестных параметров
|
|
|
|
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Первичная обработка статистических данных
2.1.1. Записать выборку (5, 3, 7, 10, 5, 5, 2, 10, 7, 2, 7, 7, 4, 2, 4) в виде вариационного ряда и статистического ряда, обозначив 
различные среди выборочных значений 
.
2.1.2. В эксперименте наблюдалась целочисленная случайная величина 
. Соответствующие выборочные значения оказались равными (3, 0, 4, 3, 6, 0, 3, 1). Записать их в виде статистического ряда, найти соответствующую эмпирическую функцию распределения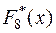 
и изобразить ее графически.
2.1.3. Пусть (0,8; 2,9; 4,4; -5,6; 1,1; -3.2) – наблюдавшиеся значения некоторой случайной величины. Построить эмпирическую функцию распределения 
и проверить, что 
, 
, 
.
2.1.4. Найти и изобразить графически эмпирические функции распределения, соответствующие следующим выборкам, представленным в виде статистических рядов:
| а) | 
| б) |
| |||||||
|
|
2.1.5. Построить эмпирические функции распределения и вычислить выборочные средние и выборочные дисперсии, соответствующие следующим выборкам, представленным в виде статистических рядов:
| а) |
| ||||||||||||
| б) |
|
2.1.6. В результате эксперимента непрерывная случайная величина приняла следующие значения (округленные до целых): (6, 17, 9, 13, 21, 11, 7, 7, 19, 5, 17, 5, 20, 18, 11, 4, 6, 22, 21, 15, 15, 23, 19, 25, 1) Построить интервальный статистический ряд, взяв 5 интервалов одинаковой длины; построить гистограмму и полигон частот.
2.1.7. Построить гистограмму и полигон частот по следующим статистическим данным, представленным в виде интервального статистического ряда:
| Номер интервала k | Границы интервала 
| Частота интервала 
|
| 0 – 2 2 – 4 4 – 6 6 – 8 8 – 10 10 – 12 12 - 14 |
Найти и построить эмпирическую функцию распределения 
, соответствующую этим сгруппированным данным; вычислить выборочное среднее и выборочную дисперсию.
|
|
|
2.1.8. Проводились опыты с бросанием 12 игральных костей. Наблюдаемую случайную величину брали равной числу костей, на которых выпало 4, 5 или 6 очков. Пусть 
- число опытов, в которых наблюдалось значение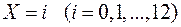 
. Ниже приведены результаты 
опытов:
| i | |||||||||||||
|
Взяв в качестве интервалов 
, построить гистограмму и полигон частот. Вычислить выборочное среднее и выборочную дисперсию, соответствующие этим данным.
2.1.9. Ниже приведены результаты измерения роста случайно отобранных 100 студентов:
| Рост, см | 154-158 | 158-162 | 162-166 | 166-170 | 170-174 | 174-178 | 178-182 |
| Число студентов |
Найти выборочное среднее и выборочную дисперсию роста обследованных студентов, построить гистограмму и полигон частот.
2.1.10. На телефонной станции производились наблюдения за числом неправильных соединений в минуту. Наблюдения в течение часа дали следующие результаты:
(3, 1, 3, 4, 2, 1, 1, 3, 2, 7, 2, 0, 2, 4, 0, 3, 0, 2, 0, 1, 3, 3, 1, 2, 2, 0, 2, 1, 4, 3,
4, 2, 0, 2, 3, 1, 3, 1, 4, 2, 2, 1, 2, 5, 1, 1, 0, 1, 1, 2, 1, 0, 3, 4, 1, 2, 2, 1, 1, 5).
Найти выборочное среднее и выборочную дисперсию числа неправильных соединений в минуту и сравнить эмпирическое распределение с распределением Пуассона.
2.1.11. Измерительным прибором, практически не имеющим систематической погрешности, было сделано пять независимых измерений некоторой величины. Получены следующие результаты:
| Номер измерения | |||||
| Результат измерения |
Найти: а) выборочную дисперсию погрешности измерения, если измеряемая величина точно известна и равна 2800; б) выборочное среднее и выборочную дисперсию, если точное значение измеряемой величины неизвестно.
|
|
|
2.1.12. Доказать, что выборочные начальные и выборочные центральные моменты 
-го порядка связаны соотношением:
.
Точечные оценки неизвестных параметров
2.2.1. Показать, что выборочное среднее 
является несмещенной и состоятельной оценкой математического ожидания наблюдаемой случайной величины .
2.2.2. Показать, что выборочная дисперсия 
не является несмещенной оценкой дисперсии наблюдаемой случайной величины . Определить смещение оценки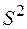 
. Является ли она асимптотически несмещенной? Показать, что несмещенной оценкой дисперсии является величина 
, называемая исправленной выборочной дисперсией.
2.2.3. Показать, что справедлива формула:
,
где 
– четвертый центральный момент случайной величины . Являются ли выборочная дисперсия 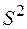и исправленная выборочная дисперсия 
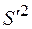состоятельными оценками наблюдаемой случайной величины ?
2.2.4. Показать, что эмпирическая функция распределения 
является несмещенной и состоятельной оценкой теоретической функции распределения 
.
2.2.5. Вычислить информацию Фишера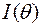 
о параметре 
, содержащуюся в одном наблюдении над случайной величиной Х, имеющей:
а) нормальное распределение 
;
б) нормальное распределение 
;
в) нормальное распределение 
;
г) гамма-распределение 
;
д) распределение Коши 
;
е) биномиальное распределение 
;
ж) распределение Пуассона 
.
2.2.6. Доказать, что выборочное среднее 
является эффективной оценкой математического ожидания наблюдаемой случайной величины Х, имеющей распределение: а) ; б) .
2.2.7. Доказать, что статистика 
является несмещенной и эффективной оценкой дисперсии наблюдаемой случайной величины , имеющей нормальное распределение .
2.2.8. Показать, что исправленная выборочная дисперсия 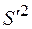является асимптотически эффективной оценкой дисперсии наблюдаемой случайной величины , имеющей нормальное распределение .
2.2.9. Пусть наблюдаемая случайная величина имеет распределение Коши . Показать, что выборочное среднее не является состоятельной оценкой параметра .
2.2.10. Показать, что в случае логистического распределения, плотность вероятностей которого при 
имеет вид:
,
справедливы утверждения:
|
|
|
а) выборочное среднее – несмещенная оценка и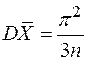 
;
б) информация Фишера 
и поэтому не является эффективной оценкой .
2.2.11. Пусть по выборке из генеральной совокупности, имеющей биномиальное распределение 
, требуется оценить функцию 
. Показать, что в данном случае несмещенных оценок не существует.
2.2.12. Пусть по одному наблюдению над случайной величиной , имеющей отрицательное биномиальное распределение 
, требуется оценить параметр . Найти оценку, удовлетворяющую условию несмещенности, и показать, что она практически бесполезна.
2.2.13. Пусть производится одно наблюдение над случайной величиной , имеющей распределение Пуассона с неизвестным параметром :
.
Показать, что в этом случае не существует несмещенных оценок параметрической функции .
2.2.14. Случайная величина имеет распределение Пуассона с неизвестным параметром . По выборке найти точечные оценки параметра по методу моментов, используя первый и второй моменты. Исследовать полученные оценки на несмещенность.
2.2.15. Случайная величина (число нестандартных изделий в партии изделий) имеет распределение Пуассона с неизвестным параметром .
Найти методом моментов оценку параметра , если обследование 
партий на наличие нестандартных изделий дало следующие результаты:
| |||||
|
|
где число нестандартных изделий в одной партии; - число партий, содержащих нестандартных изделий.
2.2.16. По выборке из генеральной совокупности, имеющей биномиальное распределение , т.е.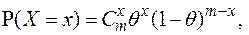 
, найти оценку неизвестной вероятности успеха по методу моментов, используя первый момент.
2.2.17. Случайная величина (число появлений события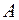 
в m независимых испытаниях) подчинена биномиальному закону распределения с неизвестным параметром . Ниже приведены результаты числа появлений события в 10 опытах по 5 испытаний в каждом:
|
| |||||
|
|
где - число появлений события 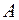в одном опыте; - количество опытов, в которых наблюдалось появлений события 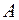. Найти методом моментов оценку параметра по этим статистическим данным.
|
|
|
2.2.18. Случайная величина Х имеет геометрическое распределение 
с неизвестным параметром , т.е. 
где 
– число испытаний, произведенных до появления события; - вероятность появления события в одном испытании. По выборке найти методом моментов оценку параметра .
2.2.19. Найти методом моментов оценку параметра геометрического распределения , если в четырех опытах событие появилось соответственно после двух, четырех, шести и восьми испытаний.
2.2.20. По выборке найти методом моментов оценку неизвестного параметра показательного распределения 
, плотность вероятностей которого 
. Исследовать полученную оценку на несмещенность.
2.2.21. Найти методом моментов по выборке точечные оценки неизвестных параметров 
и 
гамма-распределения 
, плотность вероятностей которого
.
2.2.22. Случайная величина имеет равномерное распределение на отрезке 
с неизвестными границами. По выборке найти методом моментов оценки параметров 
и 
.
2.2.23. По выборке из генеральной совокупности, имеющей биномиальное распределение , найти оценку максимального правдоподобия 
неизвестной вероятности успеха . Сравнить ее с оценкой, полученной по методу моментов (см. задачу 2.2.16).
2.2.24. Случайная величина имеет распределение Пуассона с неизвестным параметром . По выборке найти оценку максимального правдоподобия параметра и исследовать ее на несмещенность.
2.2.25. По выборке найти оценку максимального правдоподобия неизвестного параметра показательного распределения . Сравнить ее с оценкой, полученной по методу моментов (см. задачу 2.2.20).
2.2.26. Случайная величина (время безотказной работы элемента) имеет показательный закон распределения с неизвестным параметром . В результате проверки 1000 элементов были получены следующие значения среднего времени их работы:
|
| |||||||
|
|
Здесь – среднее время безотказной работы одного элемента, часов; - количество элементов, проработавших в среднем часов. Найти на основании этих данных оценку параметра по методу максимального правдоподобия.
2.2.27. По выборке из генеральной совокупности, имеющей гамма-распределение 
с плотностью вероятностей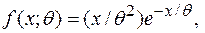 
, найти оценку максимального правдоподобия неизвестного параметра . Сравнить ее с оценкой, полученной по методу моментов (см. задачу 2.2.21).
2.2.28. Устройство состоит из элементов, время безотказной работы которых подчинено гамма-распределению 
. Испытания пяти элементов дали следующие результаты (время работы элемента в часах до отказа): (50, 60, 100, 200, 250). Найти по этим выборочным значениям оценку максимального правдоподобия неизвестного параметра .
|
|
|
2.2.29. Случайная величина , характеризующая срок службы элементов электронной аппаратуры, имеет плотность вероятностей 
(закон распределения Релея). По выборке построить оценку максимального правдоподобия неизвестного параметра . Исследовать ее на несмещенность и сравнить с оценкой, которую дает метод моментов.
2.2.30. По выборке найти оценки максимального правдоподобия неизвестных параметров распределений: а) ; б) ; в) . Проанализировать качество полученных оценок.
2.2.31. Наблюдаемая случайная величина имеет геометрическое распределение с неизвестным параметром . По выборке построить оценку максимального правдоподобия неизвестной вероятности и сравнить ее с оценкой, полученной по методу моментов (см. задачу 2.2.18).
2.2.32. Случайная величина имеет равномерное распределение на отрезке 
. По выборке построить оценку максимального правдоподобия неизвестного параметра .
2.2.33. Случайная величина имеет равномерное распределение на отрезке единичной длины 
. По выборке построить оценку максимального правдоподобия неизвестного параметра .
2.2.34. Случайная величина имеет равномерное распределение на отрезке . По выборке построить оценки максимального правдоподобия неизвестных концов отрезка и .
|
|
|
