 |
Обработка многократного измерения
|
|
|
|
Исходными данными для выполнения работы являются 14 вариаций значений, полученных при многократном измерении содержания ртути в воде Нg, мг/л. Для определения количества содержания ртути в воде произведено 60 измерений в разных частях водоема. Измерения проводились следующим образом, в разных точках водоема бралось по 1 литру воды, и определялась масса содержания в них ртути. Результаты, общее число измерений в серии многократного измерения и число повторений каждого результата, представлены в таблице № 2.
Таблица 2- исходные данные
| Результат измерений, мг/л | 15,10 | 15,15 | 15,20 | 15,25 | 15,30 | 15,35 | 15,40 | 15,45 | 15,50 | 15,55 | 15,60 | 15,65 | 15,70 | 15,75 |
| Количество повторений mi |
Требуется определить:
-Провести обработку экспериментальных данных и объяснить физический смысл результата.
-Проверить гипотезу о нормальном законе распределения случайной величины x в 1 литре воды по критерию Пирса.
- в случае подтверждения гипотезы нормального распределения следует найти доверительный интервал для истинного значения количества ртути в одном литре водоема.
Рассеяние случайных значений, зависящих от множества факторов, ни один из которых не является преобладающим, подчиняется нормальному закону распределения вероятности.
При обработке результатов многократного измерения проверяется гипотеза: подчиняется результат измерения нормальному закону распределения вероятности или нет.
Для этого выполним следующие действия:
1) Выбираем минимальное и максимальное количество содержания ртути в пробе:
Smin=15,10 мг/л
|
|
|
Smax=15,75 мг/л
Определяем количество интервалов по формуле:
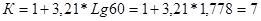, примем К=7.
Определяем шаг интервала по формуле:
Полученные интервалы заносим в таблицу № 3, и в ней же проводим вычисления середины интервала Х*i (слаживаем границы интервала и делим на 2), частоты интервала ni (количество значений в данном интервале с учетом повторений) и относительные частоты интервала Р*i (n/число измерений).
Таблица 2 – Полученные интервалы
| Интервалы | Середина X*i | Частоты ni | Относительные частоты интервала P*i |
| (15,10;15,199) | 15,15 | 0,036 | |
| (15,199;15,298) | 15,25 | 0,127 | |
| (15,298;15,397) | 15,35 | 0,2 | |
| (15,397;15,496) | 15,45 | 0,255 | |
| (15,496;15,595) | 15,55 | 0,2 | |
| (15,595;15,694) | 15,64 | 0,127 | |
| (15,694;15,793) | 15,74 | 0,055 | |
| Σ = 55 | Σ = 1 |
(15,10;15,199) = среднеарифметическое 15,15
(15,199;15,298) = среднеарифметическое 15,25
(15,298;15,397) = среднеарифметическое 15,35
(15,397;15,496) = среднеарифметическое 15,45
(15,496;15,595) = среднеарифметическое15,55
(15,595;15,694) = среднеарифметическое 15,64
(15,694;15,793) = среднеарифметическое 15,74
Вычисляем выборочную среднюю:
Х = ΣХi*p
X1 = 15,15*0,036 = 0,545
X2 = 15,25*0,127 = 1,937
X3 = 15,35*0,2 = 3,07
X4 = 15,45*0,255 = 3,94
X5 = 15,55*0,2 = 3,11
X6 = 15,64*0,127 = 1,99
X7 = 15,74*0,055 = 0,87
Σx = 0,545+1,937+3,07+3,94+3,11+1,99+0,87=15,46
Вычисляем выборочную дисперсию:
D1 = (15,15-15,46)2 *0,036 = 0,0035
D2 = (15,25-15,46)2 *0,127 = 0,0056
D3 = (15,35-15,46)2 *0,2 = 0,0013
D4 = (15,45-15,46)2 *0,255= 0,255
D5 = (15,55-15,46)2 *0,2 = 0,0016
D6 = (15,64-15,46)2 *0,127 = 0,0041
D7 = (15,74-15,46)2 *0,055 = 0,0043
Dобщее = ΣD1-7= 0,0035+0,0056+0,0013+0,255+0,0016+0,0041+0,0043 = 0,275
Вычисляем выборочное среднеквадратичное отклонение
δ = 
= 
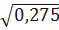= 0,524
= 15,46, 
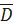=0,275 
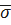=0,524
Предполагаем, что распределение нормальное, и по правилу трех сигм определяем интервал:
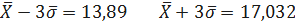
Все значения измерений попадают в данный интервал.
Проверяем гипотезу нормального распределения по критерию Пирсона. Данные представлены в таблице 3.
Таблица 3 – Теоретические и эмпирические частоты
| Интервалы, мм | 15,10; 15,199 | 15,199; 15,298 | 15,298; 15,397 | 15,397 15,496 | 15,496 15,595 | 15,595 15,694 | 15,694 15,793 | ∑ | |
| Теоретические частоты, Ni | |||||||||
| Эмпирические частоты, ni | |||||||||
|
|
|
Pi=(a<x<b)=φ 
1. Pi=(15,10;15,199)=φ 
N=55*x=55*0,06=~3
2. Pi=(15,199;15,298)=φ 
N=55*0,1=~5
3. Pi=(15,298;15,397)=φ 
N=55*0,07=~4
4. Pi=(15,397;15,496)=φ 
N=55*0,02=~1
5. Pi=(15,496;15,595)=φ 
N=55*0,07=~4
6. Pi=(15,595;15,694)=φ 
N=55*0,07=~4
7. Pi=(15,697;15,793)=φ 
N=55*0,2=~11
При использовании критерия Пирсона за меру отклонения принимается
= 16.53
Затем сравниваем табличное значение x2 с рассчитанным значениям x2 с заданным уровнем значимости, равным 0,95 и количеством степеней свободы, определенным по формуле для нормального закона распределения
m=K-1-2=7-3=4
Табличное значение составило 9,5
Так как не соблюдается условие
x2 < x2 табличное
15.67<9.5
Гипотеза о нормальном распределении не подтвердилась, поэтому нельзя сделать оценку истинного количества содержания ртути в одном литре воды
Выводы: При обработке результатов многократных равноточных измерений мы установили, что условие x2 < x2 не выполняется и закон о нормальном распределении принимать нельзя. Доверительный интервал рассчитать не удалось.
Для выполнения данного условия, и принятия закона о нормальном распределении нужно провести большее количество испытаний.
Ситуационная задача 13
Мною был приобретен билет на самолет Хабаровск – Москва. Когда я приехал в аэропорт, то выяснил, что рейс откладывается из за нелетной погоды. В аэропорту я встретил товарища, у которого был отложен рейс Хабаровск – Иркутск по причине отсутствия топлива. В результате переноса времени рейса мы были вынуждены несколько часов провести в аэропорту. В последствии мы обратились в суд с иском о возмещении морального вреда. Иск моего товарища суд удовлетворил, а мне отказал. Правомерно ли решение суда?
|
|
|
