 |
Выбор параметров процесса моделирования
|
|
|
|
Цель работы
Целью работы является компьютерное моделирование стационарного случайного процесса изменения давления в трубопроводе. Предлагается 30 вариантов заданных параметров процесса. Возможно моделирование с применением стандартной программы Simulink или на основе самостоятельно разработанной программы. В настоящих указаниях предполагается второй случай.
Исходные данные о процессе
m= 450 кПа
s = 25 кПа
a = 0.02 с-1
Примем известными математическое ожидание (среднее значение) m давления P (t) как случайной функции времени t и его корреляционную функцию K (τ). Такое описание процесса является исчерпывающим, если он относится к категории нормальных: любой набор его значений в различные моменты времени образует совокупность нормально распределенных случайных величин. Нормальность процесса далее предполагается и обеспечивается алгоритмом моделирования.
Корреляционная функция процесса K (τ) описывается выражением
K (τ)= s 2 e -a|t|, (1)
где s – стандартное (среднее квадратическое) отклонение процесса (кПа),
а a - параметр, измеряемый в 1/с и характеризующий степень убывания корреляционной функции по мере увеличения ее аргумента τ. Последний означает интервал времени между двумя значениями процесса и исчисляется в секундах.Наряду с приведенными используются следующие понятия.
Центрированный процесс 
, получающийся из исходного вычитанием из его значений математического ожидания:
= P (t) – m. (2)
Дисперсия процесса D, равная квадрату стандартного отклонения:
D = s 2. (3)
Коэффициент вариации v – отношение стандартного отклонения к математическому ожиданию:
v = s/m. (4)
Коэффициент вариации часто выражают в процентах; тогда к отношению в правой части добавляется множитель 100.
|
|
|
Нормированная корреляционная функция (НКФ) ρ (τ), получаемая путем деления K (τ) на дисперсию
ρ (τ) = K (τ)/ D. (5)
Кроме того, будет использован показатель, обычно именуемый интервалом корреляции τ кор – значение τ, по достижении которого корреляционная функция не выходит более из «коридора» 
0.01 s 2. Для корреляционной функции вида (1) приближенное значение τ кор составляет
τ кор = 5/ a. (6)
Параметры a или τ кор позволяют судить о степени хаотичности или, напротив, регулярности процесса: чем больше a (чем меньше τ кор), тем хаотичнее поведение процесса,,степень его изменчивости на выделенных промежутках времени.
При подстановке исходных данных получаем следующие значения:
K (τ)= s 2 e -a|t| K (τ)=625 e -0.02|t| K (τ)= 4.21
D = s 2. D = 625
v = s/m. v= 0.05
τ кор = 5/ a. τ кор = 250
ρ (τ) = K (τ)/ D. ρ (τ) = 0.007
Основной алгоритм
Для воспроизведения процесса в работе применяется так называемая АРСС-модель (модель «авторегрессии–скользящего среднего»). Она использует алгоритм, простейшая модификация которого, соответствующая корреляционной функции (1), может быть представлена в виде следующих трех ступеней.
1). Выбирается достаточно малый промежуток времени Δ t и время моделирования T м, в течение которого воспроизводится процесс. Назначается последовательность равноотстоящих на Δ t моментов времени
ti = i Δ t (i = 0, 1, 2,…, n), (7)
общее количество которых, не считая стартового значения t 0 = 0, равно
n = T м /Δ t. (8)
2). Выбирается стартовое значение центрированного процесса 
(можно взять его равным 0), а остальные значения последовательно находятся по рекуррентной формуле
, (i =1, 2, …, n), (9)
где A и B − константы, определяемые выражениями
A = e-a Δ t, (10)
B = 
, (11)
а Zi − независимые нормальные случайные величины, каждая из которых при
любом номере i находится по формуле
|
|
|
. (12)
Здесь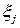 
− случайные числа из промежутка [0,1], получаемые с помощью генератора случайных чисел.
3). Каждое из значений центрированного процесса суммируется с заданным математическим ожиданием
, (i = 0,1, 2,…, n), (13)
в результате чего получается массив из (n +1) значений случайного процесса,
обладающего всеми заданными свойствами.
Выбор параметров процесса моделирования
Под этими параметрами подразумеваются Δ t и T м . Считается, что последовательные значения процесса будут достаточно близко располагаться друг от друга, если Δ t не превосходит величины
Δ t = 0.01 τ кор . (14)
Δ t = 2.5 с
Выбор времени моделирования зависит от того, с какой целью будет использоваться модель процесса. По результатам моделирования требуется найти показатели процесса и сравнить с заданными. Для этого нужно взять T м не менее, чем
T м = 50 τ кор . (15)
T м = 12500
Сравнение формул (8),(14) и (15) показывает, что величина n равна 5000 независимо от τ кор , а массив значений давления насчитывает 5001 элемент.
|
|
|
