Главная | Обратная связь | Поможем написать вашу работу!

Основные определения

Введение

Прародителями теории узлом являются К.Ф. Гаусс, который вывел замечательную интегральную формулу для числа оборотов одной замкнутой кривой в пространстве вокруг другой, а также оставил в своих записных книжках многочисленные рисунки узлов без комментариев. Систематическое развитие теории узлов началось с 1880-х годов, когда несколько математиков и физиков с большим энтузиазмом занялись составлением таблиц узлов под влиянием идей знаменитого физика У. Томпсона.

Теория узлов быстро развивается и стимулирует появление новых областей математики. В начале двадцатого века весомый вклад в теорию узлов внес знаменитый американский тополог Дж. Александер. Однако наиболее существенные достижения в теории узлов были получены лишь в конце двадцатого века. Эти достижения связаны с именами Дж. Х. Конвея, В. Джонса, В.А. Васильева, М.Л. Концевича, В.Г. Тураева, Л.Х. Кауфмана и других.

Теория узлов – одна из наиболее привлекательных областей математики. Для этого есть несколько причин:

· Теории узлов немногим более 100 лет, что является возрастом расцвета научной теории.

· Теория узлов тесно связана почти со всеми областями математики, и в ней успешно работают геометрические, алгебраческие и аналитические понятия и методы

· В теории узлов доказано много содержательных и трудных теорем, но до сих пор существует много открытых проблем с простой формулировкой, некоторые из которых стоят уже десятки лет.

Математическая теория узлов, уже во второй половине XX в. нашла разнообразные практические приложения в естественных науках: химии, биологии, физике, где узлы рассматриваются как форма самоорганизации в живой и неживой природе. Появились также предложения по использованию принципа узла в различных областях техники. Тема узлов стала проникать и в современное искусство: скульптуру, компьютерную графику, дизайн. В данной работе узлы рассматриваются как элементы декоративных плетений и их изображений, известных под общим названием «плетёный орнамент». Для изготовления плетёных изделий были необходимы узлы с регулярной структурой, что способствовало возникновению интереса к симметрии узлов.
Плетёные орнаменты и узлы обычно изготовлялись из материалов растительного и животного происхождения и были недолговечны. Возможно, что это стало стимулом для поиска других форм их художественного представления, таких как графические изображения, резьба, чеканка, литье, и т.п., что привело к возникновению плетёного орнамента, известного практически во всех человеческих культурах уже с глубокой древности.

Среди разнообразных форм плетёного орнамента широкое распространение получили структуры, выполненные из непрерывной линии, начало и конец которой соединены между собой. К ним относятся, в частности, многие кельтские, мусульманские и монгольские узлы.

Символика узлов и её отражение в традиционном мировоззрении» исследуются свидетельства того, что узлы занимали особое место в традиционной духовной культуре многих народов, выполняя роль символических объектов, применявшихся для описания космологических и метафизических представлений, ставших прообразами современных математических моделей.

Глава 1. Понятие узла, диаграммы узлов.

Основные определения

Под узлом будем понимать гладкое вложение окружности в ориентированное пространство 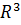(или сферу ), узлом также называют образ этого отображения.

Основным вопросом теории узлов является вопрос о том, являются ли изотопными два заданных угла. Другими словами, можно ли продеформировать один узел в другой, причем в процессе деформации не должно возникнуть самопересечений. Эта задача носит название проблемы распознавания узлов. Частным случаем является вопрос о тривиальности того или иного узла, то есть является ли заданный узел изотопным тривиальному (можно ли его развязать). Под тривиальным узлом понимается простейший узел, который может быть представлен как граница диска, гладко вложенного в 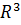. Имея перед глазами изображение тривиального узла, иногда бывает довольно трудно понять, что он тривиален.

Рис. 1.1.1. Тривиальные узлы

Для того, чтобы доказать изотопность двух узлов достаточно предъявить пошаговую изотопию, переводящую один узел в другой. Простейшими изотопиями узлов являются так называемые движения Рейдемейстера (перестройки Рейдемейстера). Известно что любая изотопия сводится к ним.

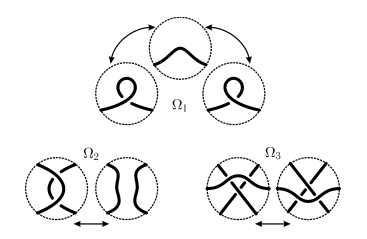
Рис. 1.1.2. перестройки Рейдемейстера

Операции, изображенные на рис. 1.1.2, называются преобразованиями Рейдемейстера и обозначаются Ω1, Ω2, Ω3. Эти преобразования соответствуют следующим ситуациям при манипуляциях с узлом:

• Ω1: появление (исчезновение) малой петли;

• Ω2: появление (исчезновение) парного перекрестка;

• Ω3: прохождение некоторой третьей ветви над перекрестком.

Следующий рисунок, представляющий процедуру развязывания, показывает, как преобразования Рейдемейстера могут участвовать в описании манипуляций с узлом.

Рис. 1.1.3. Развязывание узла с использованием преобразований Рейдемейстера

Диаграммы узлов

Обычно узлы кодируются следующим образом. Фиксируем образ, т.е. образ отображения . Рассматривает некоторую плоскость (например, 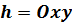) и проекцию узла на нее. Пусть – две ветви некоторого узла, проекции которых пересекаются в точке . Т.к. 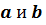не пересекаются в , два прообраза точки имеют различные -координаты.

Таким образом, можно сказать какая из ветвей проходит сверху, а какая – снизу, образуя переход ( т.е. лежит сверху ) и проход ( т.е. лежит снизу ) соответственно. Такое изображение узла на плоскости называется плоской диаграммой узла.

Рис.1.2.1. Локальная структура перекрестка

Для того, чтобы построить диаграмму заданного узла , необходимо подвергнуть его изотопии, близкой к тождественной, чтобы его проекция на выбранную плоскость стала регулярной, т.е. вектор производной нигде не обращался бы в 0 и ни какая точка не имела более двух прообразов.

а) б)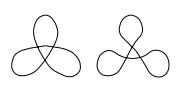

Рис. 1.2.2. а) Нерегулярная проекция узла б) Регулярная проекция узла

Плоской изотопией называется изотопия, при которой диаграмма узла, как гладкая замкнутая плоская кривая подвергается воздействию семейства взаимно однозначных преобразований плоскости, гладко зависящего от параметра.

Рис. 1.2.3. Пример плоской изотопии диаграммы

Ориентированные плоские диаграммы узлов характеризуются их диаграммами Гаусса. Диаграмма Гаусса состоит из окружности и набора хорд, соединяющих точки узла с одинаковыми проекциями на плоскость диаграммы узла.
Гауссова диаграмма порядка 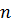– это ориентированная окружность, на которой отмечены различных точек, разбитых на пары, и на каждой из 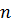хорд, соединяющих парные точки, указано направление.

Для построения гауссовой диаграммы, необходимо, на окружности, которая параметризует данную кривую отметить прообразы всех двойных точек и соединить каждую пару прообразов одной точки хордой. Направление на хордах выбирается так. На поверхности сферы есть вполне определенное положительное направление вращения. Два конца хорды соответствуют двум ветвям кривой в окрестности двойной точки. Положительные направления этих ветвей образуют угол. Так вот, направление на хорде соответствует переходу от одной стороны угла к другой в положительном направлении.

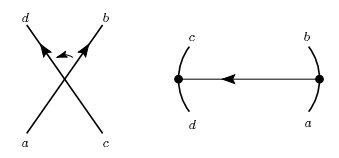
Рис. 1.2.4. Выбор направления хорды

Информация о проходах и переходах содержится в оснащенной гауссовой диаграмме. В ней дополнительно к каждой хорде ставится знак «+», если она направлена от перехода к проходу, и знак «–» в обратном случае.

Рис. 1.2.5. Локальная структура гауссовой диаграммы

Рассмотрим пример диаграммы узла и соответствующей ей диаграммы Гаусса:

Рис. 1.2.6. Диаграмма узла и его гауссова диаграмма

Аналогичным образом, длинным узлам соответствуют диаграммы Гаусса, у которых вместо окружности ориентированная прямая линия, а вместо хорд – дуги, соединяющие точки, лежащие на этой прямой линии. Каждая дуга ориентирована от прообраза прохода к прообразу перехода и снабжена знаком соответствующего перекрестка.

Воспользуйтесь поиском по сайту: