 |
Трение в поступательной паре
|
|
|
|
Тело А перемещается равномерно вверх по наклонной плоскости В (рис. 308, а).
Заданы: сила производственных сопротивлений Q (допустим, что она направлена по вертикали), угол a, образуемый наклонной плоскостью с горизонтом, и угол трения r. Требуется определить движущую силу Р, которую нужно для этого приложить к телу, и реакцию R наклонной плоскости. Зададимся углом b, определяющим направление силы Р. Реакция R при перемещении тела вверх отклоняется от нормали на угол трения в сторону, противоположную движению. Так как тело перемещается прямолинейно и равномерно, то многоугольник приложенных к нему сил должен быть замкнут. Если бы тело перемещалось неравномерно, то, приложив к нему, помимо перечисленных сил, еще и силы инерции, можно было бы рассматривать его на основании принципа кинетостатики как бы находящимся в равновесии. Построив треугольник сил, по теореме синусов получим (рис. 308, б)
Рис. 308.
Отсюда находим, что
(15.7))
(15.8)
Для практики представляют интерес следующие два случая:
а) сила Р параллельна наклонной плоскости; в этом случае b=a и из формулы (15.7)
; (15-9)
б) сила Р параллельна горизонту; в этом случае b = 0 и из выражения (15.7)
P=Q tg(a+r).
ТРЕНИЕ ВО ВРАЩАТЕЛЬНОЙ КИНЕМАТИЧЕСКОЙ ПАРЕ ПРИ НАЛИЧИИ ЗАЗОРА МЕЖДУ ЦАПФОЙ И ВКЛАДЫШЕМ ПОДШИПНИКА
Опорные части вращающихся валов и осей называют цапфами. В зависимости от направления действующей на цапфу опорной реакции различают цапфы двух видов:
1.Цапфы, в которых опорная реакция перпендикулярна к оси вращения. Такие цапфы применяют двух типов: в виде шипов, если они расположены на конце оси или вала (рис. 311), и в виде шеек, если находятся в средней их части (рис. 312).
|
|
|
2.Цапфы, в которых опорная реакция совпадает с осью вращения. Такие цапфы называют пятами. Опоры для шипов и шеек называют подшипниками, а для пят — подпятниками.
Предполагая, что шип и вкладыш подшипника работают при сухом или полусухом трении, определим сопротивление, которое возникает во вкладыше при равномерном вращении вала. Пусть на цапфу А вала, диаметр которой меньше внутреннего диаметра вкладыша В подшипника (рис. 313), действуют следующие силы: вертикальная нагрузка Q, нормальная реакция N и сила трения F. Вращающий момент М уравновешивается парой, состоящей из силы Q и равнодействующей R сил N и F, В этом случае под действием силы трения F цапфа смещается в подшипнике и занимает положение, эксцентричное относительно него. Контакт цапфы с вкладышем происходит по линии, проходящей через точку С перпендикулярно к чертежу. Для равномерного вращения шипа необходимо, чтобы момент, приложенный к шипу в направлении его вращения, | М |= Ra — Qa уравновешивался моментом трения:
Рис. 311, Рис. 312. Рис. 313.
| Mf | = Fr = fNr, т.е. | M | = | Mf |или
(15.23)
откуда
•
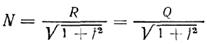Подставляя значение N в уравнение (15.23) и решая его относительно неизвестного параметра а, получим
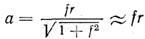
Круг радиусом а называют кругом трения. При равномерном вращении вала равнодействующая сил, приложенных к нему, касается круга трения. Если равнодействующая проходит вне круга, то вал вращается ускоренно, а если внутри круга, то вал находится в состоянии покоя или вращается замедленно.
ТРЕНИЕ КАЧЕНИЯ
При перекатывании круглого катка А (рис. 321) по плоскости В в зоне соприкосновения М катка и плоскости возникают силы, оказывающие сопротивление движению. Сопротивление, оказываемое плоскостью при чистом качении катка по ней, называют трением качения. Вопрос о физических явлениях, вызывающих трение качения, до сих пор изучен недостаточно.
Основную роль в возникновении сопротивления перекатыванию играют силы трения скольжения, всегда возникающие в месте касания катка и плоскости. Благодаря упругости тел А и В касание их происходит не по прямой линии, как это было бы, если бы эти тела были абсолютно твердыми, а по некоторой поверхности ab (рис. 322), что возможно при условии некоторой деформации катка и плоскости. При этом дуга ab на катке несколько укорачивается, а соответствующий отрезок ab на плоскости удлиняется. Отсюда следует, что процесс деформации обязательно должен сопровождаться относительным скольжением катка и плоскости на поверхности соприкасания их. Это и является источником потерь на трение скольжения. Чем тверже тела А и В, тем меньше они деформируются в месте взаимного касания, тем меньше поверхность соприкасания их и тем меньше потери на трение скольжения и сопротивление катка перекатыванию. На сопротивление перекатыванию влияют также шероховатости и неровности, неизбежно имеющиеся на поверхности как катка А, так и плоскости В. Эти неровности вызывают толчки и удары, на которые также расходуется известная часть кинетической энергии движущегося тела.
|
|
|
При качении в катке и в том теле, по которому катится каток, возникает переменное напряженное состояние, перемещающееся вместе с точкой касания. Как известно, переменное напряженное состояние в упругом теле вызывает появление колебаний. Эти колебания, возникающие при качении,— затухающие вследствие внутреннего междучастичного трения; они также поглощают часть кинетической энергии катящегося тела. Наконец, при качении часто появляются.пластические деформации. Эти деформации возникают обычно не в катке, а в плоской опоре, так как напряжение в плоскости больше, чем в круглом катке. Это подтверждается и тем, что в катке материал работает, как в своде, т. е. в условиях чрезвычайно выгодных в смысле распределения напряжений.
Пластические деформации в теле В создают следующую картину деформации в зоне касания М (рис. 323). Каток, двигаясь в направлении, указанном стрелой, деформирует, обминает часть Мa и разгружает деформированную часть b М. Но если в материале тела В возникают остающиеся деформации, то давление на каток на участке aМ больше, чем на участке М b. Впереди катка образуется как бы волна (подъем), через который ему беспрерывно надо перекатываться.
|
|
|
Рис. 321. Рис. 322. Рис. 323.
Все перечисленные причины, вместе взятые, создают при качении тела реактивный момент М D, сопротивляющийся перекатыванию, который должен быть преодолен внешними движущими силами. Опыт показывает, что момент М D при заданных условиях— размерах катка, его материале и поверхности, по которой происходит качение, обработке и т. д. — пропорционален давлению Q, приходящемуся на каток:
М D = D Q. (15.48)
Коэффициент D в этой формуле имеет размерность длины. Его называют обычно коэффициентом, или параметром, трения качения и измеряют в сантиметрах или миллиметрах.
Приводим ряд значений D:
| Условия трения | Коэффициент D, мм |
| Стальные бандажи колес железнодорожных вагонов по рельсам | 0,5—0,55 |
| Дерево по дереву | 0,5—1,3 |
| Закаленные стальные шарики и ролики в шарико- и роликоподшипниках | 0,01 |
| Колеса повозок с железными шинами по асфальту | |
| То же, по песку | 15-—30 |
Если движение катка происходит под действием пары сил, то момент трения качения определяется по формуле (15.48). Чаще каток приводится в движение горизонтальной движущей силой Р (рис. 324), приложенной на некоторой высоте h. Величину силы Р найдем на основании следующих соображений: если к равномерно движущемуся катку приложена сила Р, то в точке М вследствие равновесия возникает горизонтальная реакция, равная силе Р, но направленная в противоположную сторону. Две силы Р образуют пару. Момент Ph этой пары при равновесии тела должен равняться М D:
Ph = D Q,
откуда
(15.49)
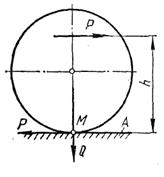Предельное значение горизонтальной реакции, которая может возникнуть в точке М,
равно /Q, где/—коэффициент трения скольжения, или коэффициент сцепления цилиндра с плоскостью.
Поэтому сила Р, найденная по формуле (15.49), должна удовлетворять условию:
Р £ fQ.
Если
Р >fQ,
Рис. 324.
то сила Р вызовет не качение, а скольжение катка. Это иногда бывает, если движущая сила прикладывается к катку слишком низко (величина h невелика). Чтобы избежать этого, надо увеличить плечо h. По формуле (15.49) сила Р при этом соответственно уменьшится. Нетрудно видеть, что наименьшее предельное значение
|
|
|
Оно соответствует условию
*
|
|
|
