Главная | Обратная связь | Поможем написать вашу работу!

Задача по машинам постоянного тока

Стр 1 из 2Следующая ⇒

МАШИНЫ ПОСТОЯННОГО ТОКА

Теоретическая часть

ЭДС машины постоянного тока:

Е = Се Ф n, (1.1)

где Е — ЭДС машины постоянного тока, В; Ф — основной магнитный поток, Вб;

n — частота вращения якоря, мин-1;

Cе — постоянная машины при расчете ЭДС.

Ce =

Np, (1.2)

60 a

где N — количество всех проводников в машине, шт.;

p — количество пар полюсов, шт.;

a — количество параллельных ветвей обмотки, шт.

В простой петлевой обмотке а=р.

Момент машины постоянного тока:

М = C м Ф I я, (1.3)

где М — момент машины постоянного тока, Н×м ;

I я — ток якоря, А;

С м — постоянная машины при расчете момента:

C = pN

м 2pa

, (1.4)

Соотношение между постоянными момента и ЭДС:

С м = Np 60 a = 60 = 9, 554, (1.5)

Се 2p a Np 2p

Уравнения равновесия напряжений:

– для генератора:

U = E - I я r я, (1.6)

где U — напряжение генератора, В;

r я — сопротивление якоря, Ом;

– для двигателя:

U = E + I я r я, (1.7)

Частота вращения двигателя постоянного тока:

– с параллельным возбуждением:

n = U - I я r я; (1.8)

Се Ф

– с последовательным возбуждением:

n = U Cе к I я

- r я Cе к

, (1.9)

где к — коэффициент пропорциональности меду током и маг- нитным потоком в двигателе последовательного возбужде- ния.

Формула, связывающая момент, мощность на валу и частоту вращения якоря:

М = 9550 Р 2. (1.10)

n

При расчете по формуле (1.10) необходимо соблюдать размерно- сти: момента (Н×м), мощности (кВт), частоты вращения (мин-1).

Потери, коэффициент полезного действия, подводимая или присое- диненная мощность иллюстрируются энергетической диаграммой (ри- сунок 1.1).

На диаграмме

Р 1 — подводимая или присоединенная мощность, Вт, двига- тель потребляет ее из сети;

U — напряжение сети, В;

I — ток двигателя, А;

Р эм — электромагнитная мощность двигателя, Вт; из рисун- ка видно:

Р 1 =UI Р эм Р 2 =UI h или Р 2=М n /9550

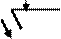
Ä Р эл

Ä Р м

Ä Р мех

Ä Р доб

Рисунок 1.1 Энергетическая диаграмма двигателя постоян- ного тока

Р эм =Р 1 - Ä Р эл, (1.11)

где Ä Р эл — электрические потери двигателя, Вт;

Ä P эл

= I в ш

+ I я я

+ I я с

+ КÄ U щ I а,

(1.12)

r

r

r

где

r ш ,r я ,r с

— сопротивления соответственно обмоток парал-

лельного возбуждения, якорной и последовательного воз- буждения, Ом;

Ä U щ

— падение напряжения на щётке, В;

I а — ток параллельной ветви, который идёт по щётке, А;

К — количество щёток, шт.

P 1 = P 2 + Ä P м + Ä P эл + Ä P мех + Ä P доб,

где Ä Р м — магнитные потери, Вт;

Ä Р мех — механические потери, Вт;

(1.13)

Ä Р доб — добавочные потери, Вт; Коэффициент полезного действия двигателя

h = Р 2.

Р 1

(1.14)

Двигатель потребляет электрическую мощность из сети, преобразует ее в механическую и через вал передает на рабочую машину. Часть мощности теряется в двигателе, что учитывается коэффициентом по- лезного действия.

У генератора наоборот: механическая мощность поступает через вал приводного двигателя (турбины), преобразуется в электриче- скую и поступает в электрическую сеть.

При построении обмоток якорь условно разрезают вдоль вала и разво- рачивают на плоскости. Коллекторные пластины и пазы нумеруют.

В простой петлевой обмотке каждая секция присоединена к двум рядом лежащим коллекторным пластинам. При укладке сек- ций за один обход якоря укладывают все секции обмотки. В резуль- тате конец последней секции должен присоединяться к началу первой, т.е. обмотка замыкается.

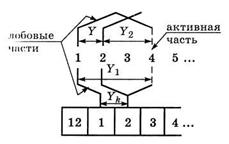
Первый частичный шаг (рис. 1.2.) Y 1 (измеряется в пазах) опре- деляется по формуле:

Y 1 =

Z ± e,

2 p

(1.15)

Рис. 1.2 Обмоточные шаги простой петлевой обмотки

где Z — число элементарных пазов якоря;

e — число дополняющее до целого.

Y 1 выбирают таким образом, чтобы ЭДС секций имели мак- симальное значение.

Результирующий шаг и шаг по коллектору равны между собой, и в простой петлевой обмотке равны единице

Y = Y к = 1.

(1.16)

Второй частичный шаг

Y 2 = Y 1 - Y.

(1.17)

В простой волновой обмотке соседние секции находятся под раз- ными парами полюсов. При укладке секций за один обход по якорю выполняется столько секций, сколько полюсов имеет машина, при этом конец последней по обходу секции присоединяют к пластине, расположенной рядом с исходной.

Результирующий шаг простой волновой обмотки (рис. 1.3) равен

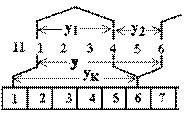Y = Z ± e.

p

Первый частичный шаг

(1.18)

Y 1 =

Y ± e.

2 p

(1.19)

Рисунок 1.3 Обмоточные ша- ги простой волновой обмотки

Второй частичный шаг

Y 2 = Y - Y 1.

(2.8)

Задача по машинам постоянного тока

Задача 1

Определить электромагнитную мощность двигателя постоянного тока кВт, если ток якоря I я = 10 А, число проводников обмотки яко-

ря N = 180 шт., магнитный поток Ф = 0,07 Вб, частота вращения

n = 1500 мин-1. Обмотка якоря простая петлевая, ширина щетки

равна ширине коллекторной пластины {ответ с точностью до двух знаков после запятой}.

Решение

Электромагнитная мощность двигателя (кВт):

Р эм =

М n.

9550

Электромагнитный момент машины постоянного тока (Н×м);

М = C м Ф I я.

Постоянная машины при расчете момента.

C м =

2 p a

Ширина щетки равна ширине коллекторной пластины, обмотка простая петлевая, поэтому количество пар параллельных ветвей равно количеству пар полюсов: а = р, — тогда

C м = 2p.

С учетом вышеизложенного

Р = N Ф I я n =

эм 2p9550

Ответ: Р эм = кВт.

Задача 2

Четырехполюсная машина постоянного тока независимого возбужде- ния имеет следующие параметры: диаметр якоря D = 0,2 м, длина якоря l = 0,4 м, число проводников обмотки якоря N = 540, индукция в воздуш-

ном зазоре B = 0,4 Тл, обмотка якоря простая петлевая, ширина щетки равна ширине коллекторной пластины. Частота вращения машины, рабо- тающей в режиме генератора, n = 1000 мин-1, напряжение на нагрузке U г = 220 В. Определить частоту вращения при работе этой же машины в режиме двигателя, если токи возбуждения и якоря остались неиз- менными, двигатель питается от сети U д = 220 В. В расчете индукцию в воздушном зазоре считать постоянной по всей длине зазора, падени- ем напряжения на щетках пренебречь {ответ с точностью до целого числа}.

Решение

Частота вращения двигателя (падением напряжения на щетках пренеб- речь)

n = U д - I я r я.

Се Ф

Сопротивление обмотки якоря определится из формулы равно- весия ЭДС генератора:

U = Е - I r = С Ф n - I r Þ r

= Се Ф n - U г.

г я я е

я я я

Подставляем полученное выражение расчета сопротивления об- мотки якоря в формулу частоты вращения двигателя:

U д - I я

Се Ф n - U г I

U д - Се Ф n + U г

n д= я =

Се Ф

Постоянная машины при определении ЭДС

C = Np

e 60 a

Количество пар полюсов — р =2 (из условия)

Ширина щетки равна ширине коллекторной пластины, обмотка

простая петлевая, поэтому количество пар параллельных ветвей равно количеству пар полюсов: а = р, — тогда

C = N

e 60

=540 =9

Так как принято допущение, что индукция в воздушном зазоре постоянная по всей длине зазора, магнитный поток можно рас- считать по формуле:

Ф = Bl t= Bl 3, 1416 D =0, 4 ´0, 4 3, 1416´0, 2 =0, 02513 Вб.

2 p 22

Частота вращения двигателя

n д 220 - 9´ 0, 02513´1000+ 220 =945, 2 мин-1

9´ 0, 02513

Ответ: n д = 945 мин-1.

Задача 3

Двигатель постоянного тока подключен к сети напряжением U =

440 В. Требуется рассчитать его магнитный поток (Вб), если его

мощность на валу Р 2 = 10 кВт, сопротивление обмотки якоря r я = 0,07 Ом, число проводников обмотки якоря N = 240, частота вращения n = 1000 мин-1. Реакцией якоря и падением напряжения на щетках пренебречь, обмотка якоря простая петлевая, одноходовая

{ответ с точностью до трех знаков после запятой}.

Решение

Из уравнений:

М = C м

Ф I я и

М = 9550 Р 2