Погрешности измерений, виды погрешностей, понятие о классе точности прибора, поверка приборов прямым и обратным ходом. Вариация показаний прибора.

 

Определение погрешности

В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.

• Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:

• Средняя квадратическая погрешность:

 

• Средняя квадратическая погрешность среднего арифметического:

Классификация погрешностей.

По форме представления:

Абсолютная погрешность — является оценкой абсолютной ошибки измерения. Вычисляется разными способами. Способ вычисления определяется распределением случайной величины . Соответственно, величина абсолютной погрешности в зависимости от распределения случайной величины может быть различной. Если — измеренное значение, а — истинное значение, то неравенство должно выполняться с некоторой вероятностью, близкой к 1. Если случайная величина распределена по нормальному закону, то обычно за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.

Существует несколько способов записи величины вместе с её абсолютной погрешностью.

• Обычно используется запись со знаком ±. Например, рекорд в беге на 100 метров, установленный в 1983 году, равен 9,930±0,005 с.
• Для записи величин, измеренных с очень высокой точностью, используется другая запись: цифры, соответствующие погрешности последних цифр мантиссы, дописываются в скобках. Например, измеренное значение постоянной Больцмана равно 1,380 6488(13)×10⁻²³ Дж/К.

Относительная погрешность — погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины (РМГ 29-99): , .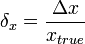

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.

Приведённая погрешность — погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле , где — нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

• если шкала прибора односторонняя, то есть нижний предел измерений равен нулю, то определяется равным верхнему пределу измерений;
• если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.

Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.

По причине возникновения:

• Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.
• Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
• Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.

В технике применяют приборы для измерения лишь с определённой заранее заданной точностью — основной погрешностью, допускаемой в нормальных условиях эксплуатации для данного прибора.

Если прибор работает в условиях, отличных от нормальных, то возникает допол-

 

нительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т. п.

Обобщённой характеристикой средств измерения является класс точности, определяемый предельными значениями допускаемых основной и дополнительной погрешностей, а также другими параметрами, влияющими на точность средств измерения; значение параметров установлено стандартами на отдельные виды средств измерений.

Классы точности средств измерений.

Класс точности – это обобщенная характеристика средств измерений, определяемая пределами допускаемых основных и дополнительных погрешностей, а также рядом других свойств, влияющих на точность осуществляемых с их помощью измерений. Классы точности регламентируются стандартами на отдельные виды средств измерения с использованием метрологических характеристик и способов их нормирования, изложенных в предыдущих главах.

Стандарт не распространяется на средства измерений, для которых предусматриваются раздельные нормы на систематическую и случайные составляющие, а также на средства измерений, для которых нормированы номинальные функции влияния, а измерения проводятся без введения поправок на влияющие величины. Классы точности не устанавливаются и на средства измерений, для которых существенное значение имеет динамическая погрешность.

Для остальных средств измерений обозначение классов точности вводится в зависимости от способов задания пределов допускаемой основной погрешности.

Пределы допускаемой абсолютной основной погрешности могут задаваться либо в виде одночленной формулы:

,

либо в виде двухчленной формулы:

,

где и выражаются одновременно либо в единицах измеряемой величины, либо в делениях шкалы измерительного прибора.

Более предпочтительным является задание пределов допускаемых погрешностей в форме приведенной или относительной погрешности.

Пределы допускаемой приведенной основной погрешности нормируются в виде одночленной формулы:

,

где число (n = 1, 0, ---1, -2…).

Пределы допускаемой относительной основной погрешности могут нормироваться либо одночленной формулой:

,

либо двухчленной формулой:

,

где – конечное значение диапазона измерений или диапазона значений воспроизводимой многозначной мерой величины, а постоянные числа q, с и d выбираются из того же ряда, что и число р.

В обоснованных случаях пределы допускаемой абсолютной или относительной погрешности можно нормировать по более сложным формулам или даже в форме графиков или таблиц.

Средствам измерений, пределы допускаемой основной погрешности которых задаются относительной погрешностью и присваивают классы точности, выбираемые из ряда чиселр и равные соответствующим пределам в процентах. Так для средства измерений с класс точности обозначается .

Если пределы допускаемой основной относительной погрешности выражаются двухчленной формулой (94), то класс точности обозначается какc/d, где числа с и d выбираются из того же ряда, что и р, но записываются в процентах. Так, из мерительный прибор класса точности 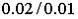характеризуется пределами допускаемой основной относительной погрешности:

.

Классы точности средств измерений, для которых пределы допускаемой основной, обозначаются одной цифрой, выбираемой из ряда для чиселр и выраженной в процентах. Если, например, , то класс точности обозначается как 0.5 (без кружка).

Классы точности обозначаются римскими цифрами или буквами латинского алфавита для средств измерений, пределы допускаемой погрешности которых задаются в форме графиков, таблиц или сложных функций входной, измеряемой или воспроизводимой величины. К буквам при этом допускается присоединять индексы в виде арабской цифры. Чем меньше пределы допускаемой погрешности, тем ближе к началу алфавита должна быть буква и тем меньше цифра. Недостатком такого обозначения класса точности является его чисто условный характер.

Класс точности средств измерений характеризует их точностные свойства, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность зависит также от метода измерений и условий их выполнения. Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведённых основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)*10ⁿ, где показатель степени n = 1; 0; −1; −2 и т. д.

По характеру проявления

• Случайная погрешность — составляющая погрешности измерения, изменяющаяся случайным образом в серии повторных измерений одной и той же величины, проведенных в одних и тех же условиях. В появлении таких погрешностей не наблюдается какой-либо закономерности, они об наруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения.

Основным свойством с.п. является возможность уменьшения искажения искомой величины путем усреднения данных. Уточнение оценки искомой величины при увеличении количества измерений (повторных экспериментов) означает, что среднее случайной погрешности при увеличении объема данных стремится к 0 (закон больших чисел). Часто случайные погрешности возникают из-за одновременного действия многих независимых причин, каждая из которых в отдельности слабо влияет на результат измерения. По этой причине часто полагают распределение случайной погрешности «нормальным». Нормальность позволяет использовать в обработке данных весь арсенал математической статистики. Однако убежденность в «нормальности» на основании не согласуется с практикой — законы распределения ошибок измерений весьма разнообразны и, как правило, сильно отличаются от нормального.

Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т. п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления).

• Систематическая погрешность — погрешность, изменяющаяся во времени по определённому закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т. п.), неучтёнными экспериментатором.

Систематическую ошибку нельзя устранить повторными измерениями. Её устраняют либо с помощью поправок или «улучшением» эксперимента.

• Прогрессирующая (дрейфовая) погрешность — непредсказуемая погрешность, медленно меняющаяся во времени. Она представляет собой нестационарный случайный процесс.

• Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора или если произошло замыкание в электрической цепи).

Надо отметить, что деление погрешностей на случайные и систематические достаточно условно. Например, ошибка округления при определенных условиях может носить характер как случайной, так и систематической ошибки.

По способу измерения:

• Погрешность прямых измерений - вычисляется по формуле

где: ; — стандартная ошибка среднего (выборочное СКО, деленное на корень из количества измерений ), а — квантиль распределения Стьюдента для числа степеней свободы и уровня значимости ; — абсолютная погрешность средства измерения (обычно это число равное половине цены деления измерительного прибора).

• Погрешность косвенных воспроизводимых измерений — погрешность вычисляемой (не измеряемой непосредственно) величины:

Если , где — непосредственно измеряемые независимые величины, имеющие погрешность , тогда:

• Погрешность косвенных невоспроизводимых измерений - вычисляется по принципу прямой погрешности, но вместо ставится значение полученное в процессе расчётов.

Поверка измерительных приборов — совокупность операций, выполняемых с целью подтверждения соответствия измерительных приборов по метрологиче-

 

ским требованиям. Поверка устройства/приборов для измерения давления может проводиться весовым способом или способом сравнения. Пружинные манометры на большое давление удобней проверять весовым методом. Поверка ма нометров на высокое давление проводится либо способом сравнения с показаниями образцовых пружинных манометров, либо смешанным способом.

 

Таблица 1

Показания проверочного прибора	Показания образцового прибора	Вариация	Погрешность
абсолютная	приведенная
°С	мВ	Прямой ход мВ	Обратный ход мВ	Абсолютная мВ	Относительная мВ	Прямой ход мВ	Обратный ход мВ	Прямой ход %	Обратный ход %
		-1,08	-0,8	-0,28	0,08	-0,61	-0,56	3,2	2,6
	3,350	3,02	2,85	-0,17	0,0289	-0,33	0,5	1,44	2,2
	6,398	6,6	6,55	-0,05	0,0025	0,202	0,152	0,22	0,7
	10,624	10,2	10,2			-0,424	-0,424	1,8	1,9
	14,570	14,3	14,4	0,1	0,01	-0,27	0,17	2,6	0,7
	17,860	18,45	18,2	-0,25	0,0625	0,59	0,34	2,9	1,5
	22,880	22,5	22,45	-0,5	0,25	0,38	0,43	1,66	1,9

 

∆абс=±(x-xдейств)

Прямой ход Обратный ход

∆абс=-1,08-0=-0,28мВ ∆абс=-0,8-0=-0,08 мВ

∆абс=3,02-3,350=-0,33 мВ ∆абс=2,85-3,350=-0,5 мВ

∆абс=6,6-6,398=0,202 мВ ∆абс=6,55-6,398=0,152 мВ

∆абс=10,2-10,624=-0,424 мВ ∆абс=10,2-10,624=-0,424 мВ

∆абс=14,3-14,570=-0,27 мВ ∆абс=14,4-14,570=-0,17 мВ

∆абс=18,45-17,860=0,59 мВ ∆абс=18,2-17,860=0,34 мВ

∆абс=22,5-22,880=-0,38 мВ ∆абс=22,45-22,880=-0,43 мВ

∆прив=(∆абс/N)*100 ∆прив=300°С или 22,880 мВ

∆прив=(1,8 /22,880)*100=3,2% ∆прив=(0,8 /22,880)*100=2,6%

∆прив=(0,33 /22,880)*100=1,44% ∆прив=(0,5 /22,880)*100=2,2%

∆прив=(0,202 /22,880)*100=0,22% ∆прив=(0,152 /22,880)*100=0,7%

∆прив=(0,424 /22,880)*100=1,8% ∆прив=(0,424 /22,880)*100=1,9%

∆прив=(0,27 /22,880)*100=2,6% ∆прив=(0,17 /22,880)*100=0,7%

∆прив=(0,59 /22,880)*100=2,9% ∆прив=(0,34 /22,880)*100=1,5%

∆прив=(0,38 /22,880)*100=1,66% ∆прив=(0,43 /22,880)*100=1,9%

∆доп=(0,25*22,880)/100=0,057

 

Вариация считается по формуле:

V = Р₁ – Р₂.

Полученные при проверке значения вариаций сравнивают с допустимым размером, численно равным границе основной допустимой погрешности проверяемого прибора.

Рис 1.4 Пружинные манометры

Манометры признаются годными по результатам проверки, если они удовлетворяют таким требованиям:

– если их основные погрешности и вариации не превышают допустимых;

– если движение стрелки в пределах всей шкалы осуществляется плавно без скачков на расстояние 1,5-3 мм от циферблата (в зависимости от диаметра корпуса);

– если стрелка после проверки возвращается к нулевой отметке с отклонением, которое не превышает допустимую погрешность, а при наличии штифта прижимается к нему.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: