 |
Законы изменения и сохранения момента импульса
|
|
|
|
МЕХАНИКА ТВЕРДОГО ТЕЛА
52.Зависит ли момент инерции однородного тела относительно оси ОО’ от: а) момента приложенных к телу сил; б) положения оси ОО’; в) формы тела; г) массы тела; д) углового ускорения? Сколько раз Вы ответили «да»?
| А) | Б) | В) | Г) |
| А) | 
| В) | 
|
| Б) | 
| Г) | 
|
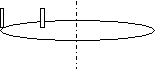
55.Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали пополам вдоль разных осей симметрии. Затем части попарно отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси  . Для моментов инерции относительно оси
. Для моментов инерции относительно оси  справедливо соотношение:
справедливо соотношение:
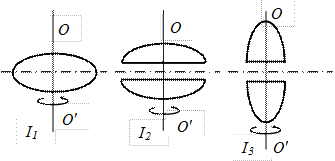
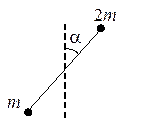 56.Твердое тело представляет собой невесомый стержень длины l, на концах которого закреплены точечные массы m и 2 m. Найдите момент инерции этого тела относительно оси, проходящей через середину стержня и составляющей угол
56.Твердое тело представляет собой невесомый стержень длины l, на концах которого закреплены точечные массы m и 2 m. Найдите момент инерции этого тела относительно оси, проходящей через середину стержня и составляющей угол  со стержнем (см. рис.).
со стержнем (см. рис.).
| А) | 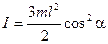
| В) | 
|
| Б) | 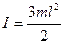
| Г) | 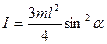
|
57.На рисунке ось О перпендикулярна плоскости чертежа. Момент инерции твердого тела (размеры и массы указаны на рисунке) относительно этой оси равен:
| А) | 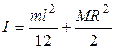
| В) | 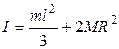
|
| Б) | 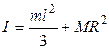
| Г) | 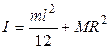
|

64.Однородный стержень длины l совершает колебания вокруг горизонтальной оси, проходящей через его конец и перпендикулярной стержню. В момент времени, когда стержень составляет угол  с вертикалью, его угловое ускорение равно:
с вертикалью, его угловое ускорение равно:
| А) | 
| Б) | 
| В) | 
| Г) | 
| Д) | 
|

65.Горизонтальный диск массы m и радиуса R свободно вращается с угловой скоростью w0 вокруг вертикальной оси, проходящей через его центр. На него сверху падает не вращающийся диск радиуса R /2 и массы m (рис.). После падения верхнего диска на нижний оба диска из-за трения между ними стали вращаться как единое целое вокруг оси, проходящей через их центры. Найдите установившуюся угловую скорость вращения дисков.
|
|
|
67. Человек, стоящий на вращающейся скамье Жуковского, держит в руках длинный шест. Как изменится угловая скорость скамьи, если человек повернет шест из вертикального положения в горизонтальное?
| А) | увеличится |
| Б) | уменьшится |
| В) | не изменится |
| Г) | может как уменьшиться, так и увеличиться в зависимости от соотношения масс человека и шеста |
68.Человек сидит в центре вращающейся по инерции вокруг вертикальной оси карусели и держит в руках длинный шест за его середину, момент сил трения пренебрежимо мал. Если он повернет шест из горизонтального положения в вертикальное, то частота вращения в конечном состоянии:
| А) | увеличится |
| Б) | уменьшится |
| В) | не изменится |
72.Однородный стержень дважды раскручивают из состояния покоя до определенной угловой скорости. В первом случае ось вращения перпендикулярна стержню и проходит через его конец, во втором – через середину стержня. Найдите отношение совершенных работ  .
.
| А) | 1/3 | Б) | 1/12 | В) | Г) | 1/4 |
 74.Однородный диск массы m и радиуса R, раскрученный до угловой скорости
74.Однородный диск массы m и радиуса R, раскрученный до угловой скорости  , падает с высоты H в ящик с песком (см. рис.). Количество теплоты, которое выделится за время движения диска, равно:
, падает с высоты H в ящик с песком (см. рис.). Количество теплоты, которое выделится за время движения диска, равно:
| А) | 
| В) | 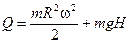
|
| Б) | 
| Г) | 
|
 76.Два маленьких массивных шарика закреплены на концах невесомого стержня длины
76.Два маленьких массивных шарика закреплены на концах невесомого стержня длины  . Стержень может вращаться в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Стержень раскрутили до угловой скорости
. Стержень может вращаться в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Стержень раскрутили до угловой скорости 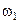 . Под действием трения стержень остановился, при этом выделилось тепло
. Под действием трения стержень остановился, при этом выделилось тепло  . Если стержень раскручен до угловой скорости
. Если стержень раскручен до угловой скорости 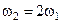 , то при остановке стержня выделится тепло
, то при остановке стержня выделится тепло
| А) | 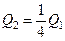
| Б) | 
| В) | 
| Г) | 
|
 77.Человек массы m стоит на краю горизонтального однородного диска массы M и радиуса R, который свободно вращается с угловой скоростью
77.Человек массы m стоит на краю горизонтального однородного диска массы M и радиуса R, который свободно вращается с угловой скоростью  . Человек переместился на расстояние
. Человек переместился на расстояние 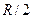 к центру диска и остановился (см. рис.). Пренебрегая размерами человека, найдите угловую скорость диска после перемещения человека.
к центру диска и остановился (см. рис.). Пренебрегая размерами человека, найдите угловую скорость диска после перемещения человека.
|
|
|
| А) | 
| Б) | 
| В) | 
|
Динамика твердого тела
Уравнение движения центра масс твердого тела.

Ускорение центра масс 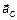 зависит от массы тела и от суммы (конечно векторной) всех сил, действующих на тело. Важно заметить, что ускорение центра масс тела не зависит от расположения точек приложения сил на теле.
зависит от массы тела и от суммы (конечно векторной) всех сил, действующих на тело. Важно заметить, что ускорение центра масс тела не зависит от расположения точек приложения сил на теле.
6.11 На гладкой горизонтальной плоскости находится однородный стержень длинной 2 м и массой 1 кг. К каждому концу стержня, приложена горизонтальная сила величиной 10 Н, перпендикулярная стержню, причем направления сил противоположны. Вычислите для этого момента величину линейного ускорения центра масс стержня.
Момент сил, действующих на твердое тело.
 6.13 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы
6.13 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
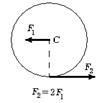 6.19 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы
6.19 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
Момент инерции твердого тела относительно постоянной оси вращения.
Определение.
Момент инерции материальной точки относительно оси вращения определяется как величина, равная произведению массы материальной точки на квадрат расстояния от этой точки до оси вращения:
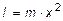 .
.
Момент инерции твердого тела относительно оси вращения – мера инертности твердого тела во вращательном движении (аналог массы в поступательном движении), определяется как величина, равная сумме моментов инерции достаточно малых фрагментов твердого тела. Достаточно малым фрагментом твердого тела является фрагмент, размеры которого малы по сравнению с расстоянием от фрагмента до оси вращения. Таким образом, этот фрагмент может быть назван материальной точкой и его момент инерции подсчитывается по формуле:
|
|
|
 ,
,
а момент инерции всего твердого тела относительно постоянной оси вращения, по формуле:
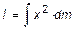 .
.
Для вычисления интеграла необходимо свести подинтегральное выражение к одной переменной величине. Это достигается, в частности, учетом как характера распределения массы тела по его объему, так и симметрии формы тела.
6.20 Найдите момент инерции тонкого кольца относительно оси, перпендикулярной плоскости кольца и проходящей через его центр. Масса кольца m, радиус кольца R.
6.22 Найдите момент инерции однородного диска относительно его оси симметрии, перпендикулярной плоскости диска и проходящей через его центр. Масса диска m, радиус диска R.
6.23 Найдите момент инерции однородного сплошного цилиндра относительно его оси симметрии, равноудаленной от всех точек боковой поверхности цилиндра. Масса цилиндра m, радиус цилиндра R.
6.25 Найдите момент инерции тонкого однородного стержня относительно оси, перпендикулярной стержню и проходящей через его конец. Масса стержня m, его длина l.
6.26 Найдите момент инерции тонкого однородного стержня относительно оси, перпендикулярной стержню и проходящей через его середину. Масса стержня m, его длина l.
Момент инерции твердого тела относительно постоянной оси вращения.
Теорема о параллельных осях (теорема Штейнера).
Теорема связывает момент инерции 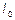 относительно произвольной оси с моментом инерции
относительно произвольной оси с моментом инерции  относительно параллельной ей оси, проходящей через центр масс твердого тела:
относительно параллельной ей оси, проходящей через центр масс твердого тела:
 .
.
Здесь m - масса тела, a – расстояние между осями.
6.31 Найдите момент инерции тонкого кольца относительно оси, перпендикулярной плоскости кольца и проходящей через любую точку его окружности. Масса кольца m, радиус кольца R.
6.32 Найдите момент инерции однородного диска относительно оси, перпендикулярной плоскости диска и проходящей через его край. Масса диска m, радиус диска R.
6.33 Найдите момент инерции тонкого однородного стержня относительно оси, перпендикулярной стержню и проходящей через его конец, если известно, что момент инерции стержня относительно параллельной оси, проходящей через центр стержня, находится по формуле  . Масса стержня m, его длина l.
. Масса стержня m, его длина l.
|
|
|
6.39 Найдите момент инерции тонкой однородной прямоугольной пластинки относительно оси, перпендикулярной ее плоскости и проходящей через ее центр. Масса пластинки m, длины ее сторон a и b.
Момент инерции твердого тела относительно постоянной оси вращения.
Теорема о взаимно перпендикулярных осях.
Момент инерции плоского тела относительно произвольной оси Z, перпендикулярной его плоскости, равен сумме моментов инерции относительно двух взаимно перпендикулярных осей X и Y, лежащих в плоскости тела и пересекающихся с осью Z:
 .
.
6.42 Момент инерции тонкого кольца относительно оси Z, перпендикулярной плоскости кольца и проходящей через его центр равен  . Масса кольца m, радиус кольца R. Найдите момент инерции кольца
. Масса кольца m, радиус кольца R. Найдите момент инерции кольца  относительно оси X, совпадающей с диаметром кольца.
относительно оси X, совпадающей с диаметром кольца.
6.43 Момент инерции однородного диска относительно оси Z, перпендикулярной плоскости диска и проходящей через его центр равен 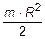 . Масса диска m, радиус диска R. Найдите момент инерции диска
. Масса диска m, радиус диска R. Найдите момент инерции диска  относительно оси X, совпадающей с диаметром диска.
относительно оси X, совпадающей с диаметром диска.
6.44 Момент инерции тонкой однородной прямоугольной пластинки относительно оси Z, перпендикулярной ее плоскости и проходящей через одну из ее вершин равен 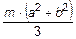 . Масса пластинки m, длины ее сторон a и b. Найдите момент инерции пластинки
. Масса пластинки m, длины ее сторон a и b. Найдите момент инерции пластинки  относительно оси X, совпадающей с ее стороной a.
относительно оси X, совпадающей с ее стороной a.
6.45 Момент инерции тонкой однородной прямоугольной пластинки относительно оси Z, перпендикулярной ее плоскости и проходящей через одну из ее вершин равен 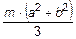 . Масса пластинки m, длины ее сторон a и b. Найдите момент инерции пластинки
. Масса пластинки m, длины ее сторон a и b. Найдите момент инерции пластинки  относительно оси Y, совпадающей с ее стороной b.
относительно оси Y, совпадающей с ее стороной b.
ЗАКОНЫ ИЗМЕНЕНИЯ И СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
Момент силы.
Моментом силы относительно точки называется физическая величина, равная векторному произведению радиус-вектора точки приложения силы на вектор силы:
 .
.
Для модуля момента силы имеем
 .
.
Плечом l силы 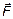 относительно точки O называется расстояние l от точки O до линии действия силы
относительно точки O называется расстояние l от точки O до линии действия силы 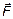 :
:
 .
.
5.1. К материальной точке, радиус – вектор которой относительно начала координат O равен  , приложена сила
, приложена сила 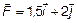 . Вычислите момент
. Вычислите момент 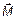 и плечо l силы
и плечо l силы 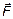 относительно точки O.
относительно точки O.
5.3. К материальной точке, радиус – вектор которой относительно начала координат O равен  , приложена сила
, приложена сила 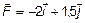 . Вычислите момент
. Вычислите момент 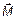 и плечо l силы
и плечо l силы 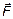 относительно точки O.
относительно точки O.
5.4. К материальной точке, радиус – вектор которой относительно начала координат O равен  , приложена сила
, приложена сила 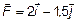 . Вычислите момент
. Вычислите момент 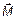 и плечо l силы
и плечо l силы 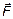 относительно точки O.
относительно точки O.
|
|
|
Момент импульса материальной точки.
Моментом импульса материальной точки относительно точки O называется физическая величина, равная векторному произведению радиус-вектора материальной точки на вектор импульса материальной точки:
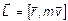 .
.

Для модуля момента импульса имеем
 .
.
5.7. Радиус – вектор материальной точки относительно начала координат O равен  . Импульс этой материальной точки равен
. Импульс этой материальной точки равен  . Вычислите момент импульса
. Вычислите момент импульса  материальной точки относительно точки O.
материальной точки относительно точки O.
5.9. Радиус – вектор материальной точки относительно начала координат O равен  . Импульс этой материальной точки равен
. Импульс этой материальной точки равен 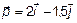 . Вычислите момент импульса
. Вычислите момент импульса  материальной точки относительно точки O.
материальной точки относительно точки O.
5.10. Радиус – вектор материальной точки относительно начала координат O равен  . Импульс этой материальной точки равен
. Импульс этой материальной точки равен  . Вычислите момент импульса
. Вычислите момент импульса  материальной точки относительно точки O.
материальной точки относительно точки O.
Уравнение моментов  или закон изменения момента импульса.
или закон изменения момента импульса.
5.11. Радиус – вектор материальной точки относительно начала координат O равен 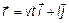 . Импульс этой материальной точки равен
. Импульс этой материальной точки равен  . Здесь
. Здесь 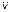 - величина постоянной скорости материальной точки. Найдите момент импульса
- величина постоянной скорости материальной точки. Найдите момент импульса  материальной точки относительно точки O. Затем найдите производную
материальной точки относительно точки O. Затем найдите производную 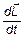 . После этого определите вектор силы, действующей на материальную точку и, наконец, найдите момент силы относительно начала координат O. Теперь убедитесь в справедливости уравнения моментов.
. После этого определите вектор силы, действующей на материальную точку и, наконец, найдите момент силы относительно начала координат O. Теперь убедитесь в справедливости уравнения моментов.
5.13. Радиус – вектор материальной точки относительно начала координат O равен  . Импульс этой материальной точки равен
. Импульс этой материальной точки равен  . Здесь
. Здесь 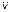 и ω- постоянные величины. Найдите момент импульса
и ω- постоянные величины. Найдите момент импульса  материальной точки относительно точки O. Затем найдите производную
материальной точки относительно точки O. Затем найдите производную  . После этого определите вектор силы, действующей на материальную точку и, наконец, найдите момент силы относительно начала координат O. Теперь убедитесь в справедливости уравнения моментов.
. После этого определите вектор силы, действующей на материальную точку и, наконец, найдите момент силы относительно начала координат O. Теперь убедитесь в справедливости уравнения моментов.
5.14. Небольшое тело массой m брошено со скоростью 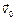 под углом a к горизонту в однородном поле сил тяжести (ускорение свободного падения равно
под углом a к горизонту в однородном поле сил тяжести (ускорение свободного падения равно  ). Найдите момент импульса
). Найдите момент импульса  материальной точки относительно стартовой точки O. Затем найдите производную
материальной точки относительно стартовой точки O. Затем найдите производную 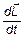 . После этого определите вектор силы, действующей на материальную точку и, наконец, найдите момент силы относительно точки O. Теперь убедитесь в справедливости уравнения моментов.
. После этого определите вектор силы, действующей на материальную точку и, наконец, найдите момент силы относительно точки O. Теперь убедитесь в справедливости уравнения моментов.
5.18. Однородный шар массы m и радиуса R начинает скатываться без скольжения по наклонной плоскости, составляющей угол a с горизонтом. Найдите зависимость от времени модуля момента импульса шара относительно точки касания в начальный момент времени.
Сохранение момента импульса.
Если импульс момента силы 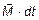 , вычисленный относительно некоторой точки равен нулю, то момент импульса, вычисленный относительно той же точки, сохраняется:
, вычисленный относительно некоторой точки равен нулю, то момент импульса, вычисленный относительно той же точки, сохраняется:
если  , то
, то 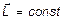 .
.
|
|
|


