 |
Математическая модель задачи
|
|
|
|
Лабораторная работа № 2
МАТРИЦЫ И ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Цель: Освоить основы матричных вычислений, способы решения систем линейных уравнений в среде табличного процессора Microsoft Ecxel
Задание № 1. Выполните операции с матрицами
1. Задайте две матрицы А и В одинакового размера (4*4), содержащие различные элементы.
2. Найдите определители для этих матриц.
3. Найдите сумму этих двух матриц и поместите ее в матрицу S.
4. Задайте матрицу C, количество строк этой матрицы должно быть равно количеству столбцов А.
5. Найдите произведение матриц А и С и поместите результат в матрицу Р.
6. Транспонируйте матрицу Р.
Задание № 2. Решить систему линейных уравнений
Найти решение системы линейных уравнений матричным способом. В этом случае для нахождения неизвестных переменных X находят обратную матрицу для исходной матрицы А и умножают ее на матрицу свободных членов В (AX=B, тогда X=A1B).
| 1. | -2x1+3x2 +6x3=1200 4x1 -5x2 +7x3=2600 x1 +2x2 -3x3=3800 | 6. | 7x1+4x2 =4151 -2x1 +x2 +7x3=3250 7x1 -3x2 +6x3=2864 |
| 2. | -5x1+x2 +2x3=2639 3x1 +9x3=2600 10x1 +2x2 -7x3=3800 | 7. | 5x1+3x3=4085 -2x2 +7x3=2441 x1 +3x2 -x3=2866 |
| 3. | 2x1+8x2 +5x3=4707 6x1 +3x2 +10x3=4483 7x2 +8x3=3920 | 8. | 8x1+7x2 +5x3=2064 6x1 +8x2 +x3=1656 x1 +4x2 +7x3=1665 |
| 4. | 8x1-2x2 +4x3=3908 8x1 -2x2 +x3=3777 -3x1 +2x2 -2x3=3734 | 9. | 8x1+3x2 +9x3=2631 10x1 +6x2 +2x3=1996 -x2 +9x3=1521 |
| 5. | 7x1-2x3=2305 -3x1 +2x2 +5x3=3997 8x1 -1x2 +5x3=2201 | 10. | -2x1+2x2 +7x3=2642 6x1 -2x2 +3x3=4013 3x1 +x3=3803 |
Задание № 3. Решить задачу линейного программирования с помощью инструмента «Поиск решения»
Для изготовления трех видов изделий А,В и С используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования, общий фонд рабочего времени каждого из типов используемого оборудования, а также прибыль от реализации одного изделия каждого вида указаны в таблице:
|
|
|
| Тип оборудования | Затраты времени (станко/ч) на обработку одного изделия вида | Общий фонд рабочего времени оборудования (ч) | ||
| А | В | С | ||
| Фрезерное | ||||
| Токарное | ||||
| Сварочное | ||||
| Шлифовальное | ||||
| Прибыль | ||||
| Количество |
Требуется определить, сколько изделий и какого вида следует изготовить предприятию, чтобы прибыль от их реализации была бы максимальной.
Образец решения задачи
Дано: для изготовления четырех видов продукции используется три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта представлены в таблице
| Тип сырья | Нормы расхода сырья не одно изделие | Запасы сырья | |||
| А | Б | В | Г | ||
| I | |||||
| II | |||||
| III | |||||
| Цена изделия |
Найти: оптимальный производственный план, который максимизирует доход предприятия.
Математическая модель задачи
Задача принятия решения по оптимальному использованию ресурсов предприятия при производстве товаров постановке описывается следующим образом. Требуется определить такой план производства товаров, реализация которого обеспечит предприятию максимальный валовой доход.
Рассмотрим предприятие, выпускающее n видов товаров: 
Для производства этих товаров имеется m видов сырья: 
При производстве товаров затрачивается: 
- единиц сырья, где 
ресурс, затрачиваемый на j-тый товар. Стоимости товаров равны соответственно 
Найти оптимальный план по выпуску товаров, т.е. количество товаров, которое обеспечивает максимальный доход.
Обозначим количество выпускаемых товаров n-ого вида при оптимальном плане: 
Опишем целевую функцию:
Данная целевая функция с учетом исходных данных перепишется:
|
|
|
Из-за ограниченности ресурсов в любой экономической системе, необходимо на целевую функцию наложить соответствующие ограничения. Количество ресурса первого вида, затрачиваемого на всю продукцию товаров, ограничивается фактическим количеством этого ресурса:
Аналогично, получим для всех видов ресурсов:
…………………………………..
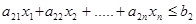
Так как количество выпускаемого товара каждого вида не может быть меньше нуля, то наложим ещё одно условие:
Сформулируем экономико-математическую модель:
Требуется определить такие показатели плана 
, 
, 
, 
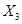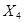, которые обеспечивают максимальный валовой доход:
При ограничениях на ресурсы:
,
,
,
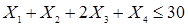Показатели не должны быть отрицательными 
, 
, 
, 
.
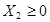Сформулированная задача принятия решения относится к классу задач линейного программирования. Решение задач линейного программирования с помощью настройки «Поиск решений» в среде EXCEL
Создадим форму для ввода условий задачи и введем исходные данные в созданную форму. Получим результат, показанный ниже, который является комментарием к решению задачи.
В ячейках В3:Е3 - будет помещено оптимальное значение плана, F4 – оптимальное значение целевой функции. Введем целевую функцию дохода в ячейку F4. Для этого удобно использовать функцию СУММПРОИЗВ(). В качестве аргументов ввести массив 1 –количество произведенной продукции (В$3:Е$3), в массив 2 ввести цены изделий (В4:Е4).
Затем ввести зависимость для левых частей ограничений. Использовать ту же функцию СУММПРОИЗВ(), а в качестве аргументов массив с количеством продукции и массив с затратами сырья каждого вида. После этого используйте «Поиск решения».
|
|
|
