 |
Задание для самостоятельного выполнения
|
|
|
|
Основы статистической обработки данных
В табл. № 1 представлены экспериментальные данные, полученные после медицинского обследования 100 студентов. Необходимо оценить числовые характеристики выборки, проанализировать форму распределения частот.
Таблица 1 -Результаты измерения веса студентов
1. Построить в Excel гистограмму распределения признаков по частотам и полигон частот. Для этого:
· найти min и max значения в выборочной совокупности (с помощью статистических функций Excel);
· размах варьирования: Rx = max - min;
· число интервалов: k» 1+3,2* lg(n), где n – количество данных в выборке.
· создать массив признаков и посчитать для них частоту.
2. Используя данные выборки студентов, рассчитать:
· среднее арифметическое;
· медиану;
· моду;
· дисперсию;
· среднее квадратичное отклонение;
· эксцесс;
· асимметрию распределения (функция СКОС).
Рекомендации к выполнению:
Ниже в качестве образца приведен пример выполнения подобной работы. В таблице приведены числовые характеристики, которые рассчитываются с помощью функций Excel, построены полигон и гистограмма частот.
Таблица 2- Образец выполнения работы
| max | Признаки (интервалы) | Частоты | ||
| min | 46,4 | |||
| R | … | |||
| k | … | |||
| сред ар | … | |||
| медиана | … | |||
| мода | … | |||
| дисперсия | ||||
| ср. кв. откл | Сумма | |||
| эксцесс | ||||
| ассиметрия | ||||
| С(цена деления) | =R/k |
|
|
|
1. Скопировать массив данных из таблицы 1, расположенной в лабораторной работе.
2. Создать массив интервалов (количество интервалов было вами рассчитано). Первый интервал определяется как сумма минимального элемента выборки и цены деления (C), последний элемент не должен существенно превышать максимального элемента выборки.
3. Выделить ячейки под массив частот (пометить доступными способами). Этих ячеек должно быть столько же, сколько ячеек отведено под массив интервалов.
4. Вызвать мастер функций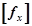 
. (Под двоичным_массивом здесь понимается массив_интервалов). Ввести координаты массива данных (вариант) и массива интервалов.
5. После указания всех аргументов функции нажать комбинацию: Ctrl+Shift+Enter. После этого функция ЧАСТОТА заполнит весь выделенныймассив.
Для построения частот используется функция
Excel ЧАСТОТА (массив_данных; массив_интервалов). Эта функция относится к классу статистических и производит операции над массивами.
Массив_данных — ячейки с данными выборки.
Массив_интервалов — ячейки, содержащие значения интервалов.
Результатом выполнения функции ЧАСТОТА является массив, содержащий частоты вариантов, попадающие в указанные интервалы. На основе этого результирующего массива и строятся гистограммы и полигоны.
Полигон и гистограмма частот строятся по значениям частоты.
Доверительный интервал генеральной средней рассчитывается по формуле:
,
где 
Для небольшого объема выборки меньше 100 элементов используют формулу
γ – доверительная вероятность (обычно равна 0,9, 0,95 или 0,99).
Ф-1 - обратное значение функции стандартного нормального распределения. Значения этой функции для трех вероятностей (0,9, 0,95 или 0,99) соответствуют: 1,64, 1,96 и 2,58.
|
|
|
Доверительный интервал в Excel можно рассчитать и с помощью функции:
ДОВЕРИТ (альфа, станд-отклон, размер),
где альфа – уровень значимости или доверительный уровень, который в принятых выше обозначениях равен 1- γ, т.е. вероятность того, что математическое ожидание окажется за пределами доверительного интервала (при вероятности 0,95, альфа равно 0,05);
стандартное_откл – среднее квадратичное отклонение выборочных данных;
размер – размер выборки (n).
Задание для самостоятельного выполнения
Пусть дана последовательность значений некоторого признака: 14; 14; 25; 15; 12; 8; 18; 23; 14; 11; 18; 18; 12; 29; 16; 17; 13; 15; 20; 10; 17; 16; 18; 16; 14; 9; 15; 13; 20; 28; 9; 20. Выполните статистическую обработку данных по следующей схеме:
1) выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения;
2) составить равноинтервальный вариационный ряд, разбив всю вариацию на k интервалов. Число интервалов определяем по формуле Герберта Стёрджеса (Herbert Arthur Sturges): k = 1+3,322*lgN;
3) построить гистограмму распределения;
4) найти числовые характеристики выборочной совокупности: характеристики положения (выборочную среднюю, моду, медиану); характеристики рассеяния (выборочную дисперсию, среднеквадратическое отклонение);
5) найти доверительный интервал для генеральной средней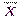 
. Принять уровень значимости α = 0,05.
Контрольные вопросы:
1. Что называется генеральной совокупностью?
2. Приведите пример генеральной совокупности, исследуемого признака и варианта.
3. Дайте понятие частоты.
4. Что представляет собой полигон частот? Какую информацию можно получить, исследуя полигон частот?
5. Какие формы распределений существуют и чем они отличаются друг от друга? В чем разница между теоретическими и экспериментальными распределениями?
6. Что называется медианой и как ее определяют?
7. Что такое мода?
8. Как определить дисперсию экспериментального распределения?
9. Что характеризует асимметрия выборки?
10. Как рассчитывается эксцесс выборки?
11. При каком значении эксцесса полигон частот наиболее заострен?
|
|
|
|
|
|
