 |
Обработка многократного измерения
|
|
|
|
Условия:
Для определения количества содержания ртути в воде произведено 60 измерений в разных частях водоема, измерения проводились следующим образом: в разных частях водоема бралось по одному литру воды и определялась масса содержимого в них ртути. Результаты, общее число измерений в серии многократного измерения и число повторений каждого результата представлены в табл. 1.
2) Проверить гипотезу о нормальном законе распределения случайной величины, l- зазор между стеновыми панелями, мм.
3) В случае подтверждения гипотезы нормального распределения следует найти доверительный интервал для истинного значения зазора между стеновыми панелями в строящемся доме.
Таблица 1 – Исходные данные
| Результаты измеренийSi | 21,25 | 21,30 | 21,35 | 21,40 | 21,45 | 21,50 | 21,55 | 21,60 | 21,65 | 21,70 | 21,75 | 21,80 | 21,85 | 21,90 |
| Число повторений mi |
Выбираем минимальный и максимальный интервал:
хmin=21,25
хmax=21,90
1) Определяем число интервалов разбиения:
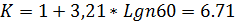
2) Определяем шаг интервала (диапазон):

3)Определяем величину интервалов, середину интервала, частоты, относительные частоты. Результаты сводим в таблицу 2.
Таблица 2 – Полученные интервалы
| Интервалы | 20,25; 21,35 | 20,35;21,45 | 20,45;20,54 | 21,54;21,64 | 21,64;21,74 | 21,74;24,84 | 21,84;21,93 | ∑ |
| Середина X*i | 21,30 | 21,4 | 21,5 | 21,6 | 21,7 | 21,8 | 21,9 | |
| Частоты ni | ||||||||
| Относительные частоты интервала P*i | 0,05 | 0,116 | 0,217 | 0,233 | 0,2 | 0,133 | 0,05 | 0.999 |
4)Вычисляем выборочную среднюю:
|
|
|

5)Вычисляем выборочную дисперсию:

6) Вычисляем выборочное среднеквадратичное отклонение:
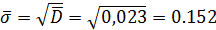
 = 21.558
= 21.558  =0,023
=0,023  =0,152
=0,152
Предполагаем, что распределение нормальное, и по правилу трех сигм определяем интервал:


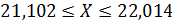
Все значения измерений попадают в данный интервал.
Проверяем гипотезу нормального распределения по критерию Пирсона. Данные представлены в таблице 3.
Таблица 3 – Теоретические и эмпирические частоты
| Интервалы, мм | 20,25; 21,35 | 20,35;21,45 | 20,45;20,54 | 21,54;21,64 | 21,64;21,74 | 21,74;24,84 | 21,84;21,93 | ∑ |
| Теоретические частоты, Ni | ||||||||
| Эмпирические частоты, ni |
Теоретические частоты в интервалы определяются по формуле:

где Pi – теоретическая вероятность попадания отдельного значения интервала. Которая определяется по формуле:
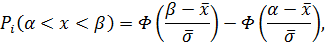
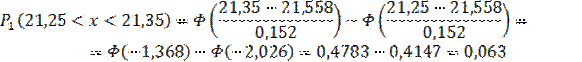
 60
60 
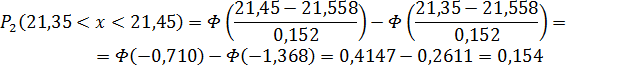
 60
60 
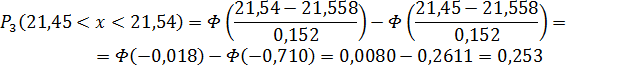
 60
60 

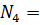 60
60 

N5 =60 
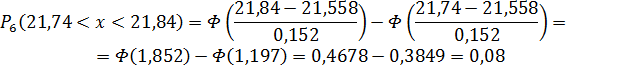
 60
60 

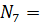 60
60 
При использовании критерия Пирсона за меру отклонения принимается:

Затем сравниваем рассчитанное значение χ2 с табличным значением χ2 с заданным уровнем значимости равным 0,95 или α=0,05 и количеством степеней свободы определенным по формуле для нормального закона распределения:
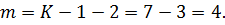
где K – число интервалов.
Табличное значение χ20,05;4 составило = 9,5.
Так как уравнение соблюдается:
χ2< χ20,05;4
0<9,5
То, гипотеза о нормальном распределении подтвердилась, поэтому можно сделать вывод.
Вывод:
При обработке результатов многократных равноточных измерений мы установили, что условие χ2< χ20,05;4 выполняется и закон о нормальном распределении принимать можно. Доверительный интервал рассчитать удалось. Для выполнения данного условия, и принятия закона о нормальном распределении проведено достаточное количество испытаний.
Ситуационная задача 14
|
|
|
Многие строительные фирмы заключают с гражданами договоры об участии в долевом строительстве дома. Просим разъяснить, регулируются ли такие отношения Законом РФ «О защите прав потребителей» и может ли потребитель потребовать взыскания неустойки в соответствии с законом при соблюдении сроков выполнения обязательств, указанных в договоре
Ответ:1) Закон о защите прав потребителей применяется к любым сделкам по привлечению средств граждан на строительство дома. В том случае, если судом установлено, что сторонами действительно имелся в виду договор участия в долевом строительстве, то подлежат применению нормы как закона об участии в долевом строительстве, так и нормы закона о защите прав.
2 Так, согласно ч. 1 ст. 6 ФЗ «О долевом участии в строительстве», застройщик обязан передать участнику долевого строительства объект долевого строительства не позднее срока, который предусмотрен договором и должен быть единым для участников долевого строительства, которым застройщик обязан передать объекты долевого строительства, входящие в состав многоквартирного дома и (или) иного объекта недвижимости или в состав блок-секции многоквартирного дома, имеющей отдельный подъезд с выходом на территорию общего пользования.
Частью 2 ст. 6 ФЗ «О долевом участии в строительстве» установлено, что в случае нарушения, предусмотренного договором срока передачи участнику долевого строительства объекта долевого строительства, застройщик уплачивает участнику долевого строительства неустойку (пени) в размере одной трехсотой ставки рефинансирования Центрального банка Российской Федерации, действующей на день исполнения обязательства, от цены договора за каждый день просрочки.
Литература:
1. В. И. Турчанинов. Метрология, стандартизация, сертификация и управление качеством в промышленности строительных материалов.
2. Абелев М. Ю. Строительный контроль и управление качеством в строительстве.
3. Радкевич Я. М. Метрология, стандартизация и сертификация (базовый курс).
|
|
|


