 |
Лекция 10. Метод функций Грина решения задачи Дирихле
|
|
|
|
Метод функций Грина решения задачи Дирихле основывается на формулах Грина. На плоскости эта формула имеет следующий вид: если функции U = U(x,y) и V = V(x,y) имеют непрерывные частные производные второго порядка в ограниченной области D и непрерывны в замкнутой области  , то
, то
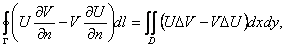
где  и
и  - производные по направлению внешней нормали к D, а кривая Г - положительно ориентирована (то есть направление интегрирования таково, что область D при интегрировании остается слева). Из этой формулы легко выводится обобщенная формула Грина
- производные по направлению внешней нормали к D, а кривая Г - положительно ориентирована (то есть направление интегрирования таково, что область D при интегрировании остается слева). Из этой формулы легко выводится обобщенная формула Грина

(43)
где С - замкнутая кривая, лежащая внутри кривой Г,а D - область, заключенная между Г и С (см. рис. 20). Кривая С также положительно ориентирована, а n1 - направление внешней нормали к D.
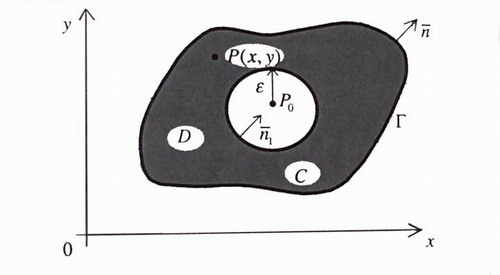
Рис. 20
Аналогичная формула имеется и в случае пространства, однако мы ее не приводим, поскольку в дальнейшем метод функций Грина подробно излагается только для плоских областей. Для искомой гармонической функции U, удовлетворяющей условию Дирихле  , и функции V = G(P, Po) - функции Грина - формула (43) будет иметь вид:
, и функции V = G(P, Po) - функции Грина - формула (43) будет иметь вид:

(44)
где С - окружность радиуса ε с центром в точке Po (см. рис.20). Остальные слагаемые в данном случае будут равны нулю, так как  и
и  в D. Вычислим интеграл
в D. Вычислим интеграл  Для этого введем полярные координаты (r, φ) с полюсом в точке Po. Тогда
Для этого введем полярные координаты (r, φ) с полюсом в точке Po. Тогда  на окружности C расстояние r = ε и dl = εdφ. Поэтому
на окружности C расстояние r = ε и dl = εdφ. Поэтому

Из определения функции Грина вытекает, что  где g(P, Po) - гармоническая функция всюду в области D. Это означает, что g(P, Po) и ее производная по нормали n1 ограничены в D, следовательно
где g(P, Po) - гармоническая функция всюду в области D. Это означает, что g(P, Po) и ее производная по нормали n1 ограничены в D, следовательно

Кроме того, функция U и ее производная  - также ограничены в D. Поэтому
- также ограничены в D. Поэтому

где α(ε) и β(ε) - ограниченные величины при 
Переходя к пределу при  , получим
, получим
|
|
|

Таким образом, из формулы (44) с учетом граничного условия  вытекает
вытекает
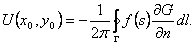
(45)
Эта формула дает решение задачи Дирихле для ограниченной области на плоскости, если известна функция Грина G.
В пространстве доказывается аналогичная формула, дающая интегральное представление решения задачи Дирихле, если известна соответствующая функция Грина. Она имеет вид

где Г - положительно ориентированная поверхность, ограничивающая область D в пространстве, и, f(s) - граничные значения гармонической функции.
Замечание. Метод функций Грина позволяет получать решения многих задач в областях различной формы. Однако для каждой области (а точнее, для каждого оператора, стоящего в левой части граничного условия) и для каждого уравнения нужно находить свою функцию Грина, что является часто непростой задачей. В том случае, когда функция Грина известна, например, для круга, шара или других простых областей (см. лекцию 9), решение соответствующей задачи выводится несложными вычислениями.
С помощью формулы (45) легко получается интегральная формула Пуассона для круга. Для этого нужно вычислить производную  функции Грина для круга. Рассмотрим сначала круг радиуса R с центром в начале координат (см. рис.17). Функция G(P, Po) для этого круга имеет вид (формула 42):
функции Грина для круга. Рассмотрим сначала круг радиуса R с центром в начале координат (см. рис.17). Функция G(P, Po) для этого круга имеет вид (формула 42):

Так как направление внешней нормали к Г совпадает с направлением полярного радиуса ρ, то

На границе Г расстояние  поэтому
поэтому

Подставим полученное выражение для производной в формулу (45):

(46)
Так как точка  может быть произвольной внутри круга, обозначим ее координаты через
может быть произвольной внутри круга, обозначим ее координаты через  - полярная система координат с полюсом в точке О. Тогда окончательно формула (46) примет вид:
- полярная система координат с полюсом в точке О. Тогда окончательно формула (46) примет вид:

(47)
Из формулы (47) нетрудно получить интегральную формулу Пуассона для произвольного круга радиуса R с центром (хо, уо). Для этого преобразуем данный круг с помощью замены переменных  в круг того же радиуса, но с центром в начале координат, запишем для него формулу (47), а затем вернемся к прежним переменным. В результате будем иметь формулу
в круг того же радиуса, но с центром в начале координат, запишем для него формулу (47), а затем вернемся к прежним переменным. В результате будем иметь формулу
|
|
|
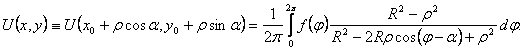
Функция  называется ядром Пуассона для круга. Отметим некоторые свойства ядра Пуассона.
называется ядром Пуассона для круга. Отметим некоторые свойства ядра Пуассона.
1. Ядро Пуассона положительно при ρ < R, при ρ = R оно всюду равно нулю, кроме точки α = φ. Вблизи точки  оно неограничено.
оно неограничено.
2. Если точка 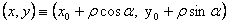 меняется внутри круга, то ядро Пуассона есть гармоническая функция от (x, у).
меняется внутри круга, то ядро Пуассона есть гармоническая функция от (x, у).
3. При ρ < R справедлива формула

(48)
Свойство 1 очевидно, так как  . На луче α = φ ядро Пуассона имеет вид
. На луче α = φ ядро Пуассона имеет вид
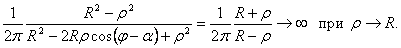
Свойства 2 и З проверяются непосредственно с помощью вычислений. Однако свойство 3 можно доказать и более красивым способом. А именно, если рассмотреть задачу Дирихле в круге радиуса R с граничным условием  , то решение такой задачи определяется формулой Пуассона (47):
, то решение такой задачи определяется формулой Пуассона (47):

С другой стороны, функция 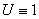 также является решением задачи Дирихле в круге с тем же граничным условием. В силу единственности решения задачи Дирихле получаем равенство (48).
также является решением задачи Дирихле в круге с тем же граничным условием. В силу единственности решения задачи Дирихле получаем равенство (48).
|
|
|


