 |
Пример экзаменационного билета
|
|
|
|
Нижнетагильский машиностроительный техникум
(факультет среднего профессионального образования)
Программа промежуточной аттестации
дисциплина «Математика»
для специальностей среднего профессионального образования
базовый уровень
технический профиль
I семестр
Составлена в соответствии с ФГОС среднего (полного) общего образования базовый уровень.
Разработчик: Ведерникова Е.В., преподаватель высшей категории.
Программа обсуждена и одобрена на заседании цикловой комиссии гуманитарных и общеобразовательных дисциплин.
Протокол № «»2011 г.
Председатель ЦК _____________ / И. Л. Вохмянина/
(подпись) (ФИО)
Заместитель директора по УМР ____________ /Гусева Е.И./
(подпись) (ФИО)
СОДЕРЖАНИЕ
стр.
1. Пояснительная записка 4
2. Критерии оценивания 7
3. Перечень примерных упражнений 9
4. Пример экзаменационного билета 16
5. Перечень наглядных пособий 18
6. Рекомендуемая литература 19
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Программа промежуточной аттестации по дисциплине «Математика» предназначена для реализации требований к ФГОС среднего (полного) общего образования, технического профиля базового уровня.
Программа составлена на основании рабочей программы по учебной дисциплине «Математика» и соответствует ФГОС среднего (полного) общего образования и «Положения о промежуточной аттестации студентов».
Вид аттестации экзамен
Форма проведения письменная
Цель промежуточной аттестации:
- выявление соответствия уровня подготовки каждого обучающегося требованиям ФГОС среднего (полного) общего образования
- выявление уровня сформированности общих компетенций, уровня усвоения знаний по основным темам курса, указанных в обязательном минимуме содержания дисциплины, уровня сформированности умений, применять эти знания для решения конкретных задач и упражнений, а также уровня достижения целей обучения математике.
|
|
|
Задачи:
- определить уровень владения и оперирования математическими понятиями и терминами;
- определить уровень сформированности математического аппарата для решения задач и упражнений;
- определить уровень понимания студентами значения курса математики в будущей профессиональной деятельности;
- определить уровень сформированности математического стиля мышления;
- выявить уровень формирования алгоритмического мышления;
- определить уровень сформированности умений обобщать, конкретизировать, анализировать, классифицировать и систематизировать;
Планируемый результат: в результате изучения
обучающийся должен:
владеть компетенциями:
- ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес;
- ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество;
- ОК 4.Осуществлять поиск и использовать информацию, необходимую для эффективного выполнения задач профессионального и личностного развития;
уметь:
- выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства;
- пользоваться оценкой и прикидкой при практических расчетах;
- проводить по известным формулам и правилам преобразования
- буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
- вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
|
|
|
- определять значение функции по значению аргумента при различных способах задания функции;
- строить графики изученных функций;
- решать уравнения, простейшие системы уравнений;
- вычислять производные элементарных функций,
- исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
- решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
знать:
- значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
- значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа,
- универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
КРИТЕРИИ ОЦЕНИВАНИЯ
Экзаменационный билет включает четыре задания по два разноуровневых упражнения в каждом.
К грубым ошибкам относятся ошибки, которые обнаруживают незнание учащимися формул, правил, основных свойств, теорем и неумение их применять, незнание приёмов решения задач, рассматриваемых в курсе математики, а также вычислительные ошибки, если они не являются опиской.
К негрубым ошибкам относятся: потеря корня или сохранения в ответе постороннего корня, отбрасывание без объяснения одного из корней и равнозначные им.
К недочетам относятся: нерациональное решение, описки, недостаточность или отсутствие пояснений, обоснований в решениях.
Если одна и та же ошибка (один и тот же недочет) встречаются несколько раз, то это рассматривается как одна ошибка (один недочет). Зачеркивания в работе (желательно, чтобы они были аккуратными) свидетельствуют о поисках решения, что считать ошибкой не следует.
|
|
|
«5» (отлично): ставится только в том случае, если работа выполнена полностью и без ошибок. Количество недочетов в такой работе не должно превышать одного.
«4» (хорошо): ставится в следующих случаях:
- работа выполнена полностью и не содержит грубых ошибок, но содержит негрубые ошибки или более двух недочетов, или негрубые ошибки или недочеты;
- семь упражнений выполнено без ошибок, а одно либо не выполнено, либо содержит ошибки;
- -правильно выполнено хотя бы по одному упражнений из каждого задания и всего решено шесть упражнений, а два либо содержат негрубые ошибки, либо одно содержит ошибку, а другое не выполнено.
«3» (удовлетворительно): ставится в следующих случаях:
- если правильно решено хотя бы по одному упражнению из каждого задания и количество недочетов не превышает двух;
- если правильно выполнено не менее 60% от объема работы и количество недочетов не превышало двух;
«2» (неудовлетворительно): ставится, если выполнено менее 60% работы.
Если в решении всей работы встречается хотя бы одна ошибка (грубая или негрубая), то недочеты при выставлении работы не учитываются.
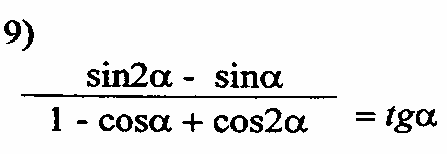
ПЕРЕЧЕНЬ ПРИМЕРНЫХ УПРАЖНЕНИЙ
Доказать тождества
1. 
2. 
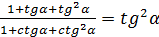
3. 
4. 
5. 
6. 
7. 
8. 
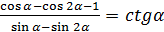
9. 
10. 
11. 
12. 
13. 
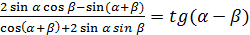
14. 
15. 
16. 
17. 
18. 
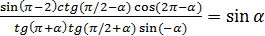
19. 
20. 
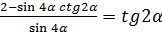
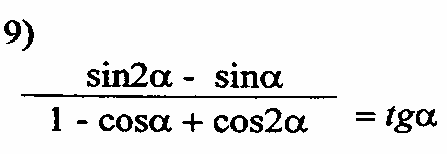
Решить уравнения
1. 
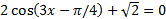
2. 
3. 
4. 
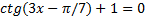
5. 
6. 
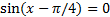
7. 
8. 
9. 
10. 
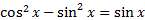
11. 
12. 
13. 
14. 
15. 
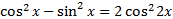
16. 
17. 
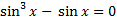
18. 
19. 
20. 
Решить уравнения
1. 
2. 
3. 
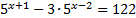
4. 
5. 
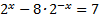
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
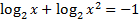
17. 
18. 
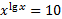
19. 
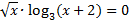
20. 
Вычислить предел функции
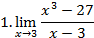
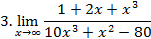
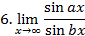
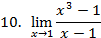
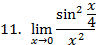
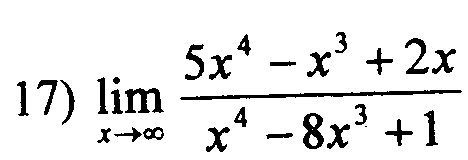
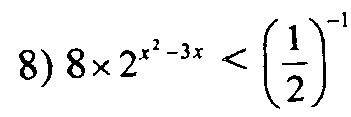
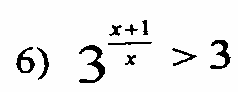
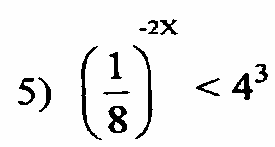
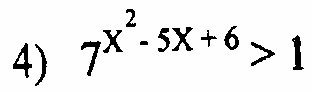
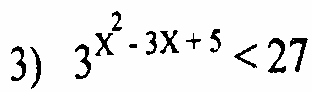
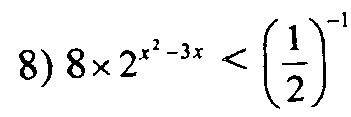
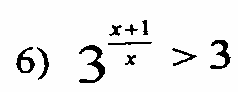
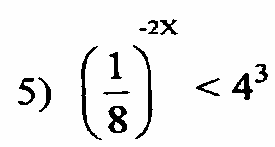
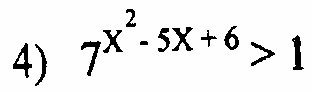
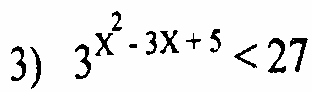Решить неравенства
1. 
2. 
3. 
4. 
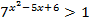
5. 
6. 
7. 
8. 
9. 
10. 
11. 
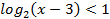
12. 
13. 
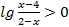
14. 
15. 
16. 
17. 
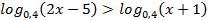
18. 
19. 
20. 
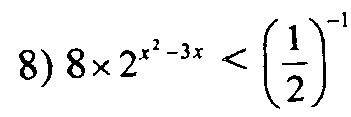
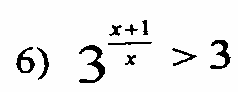
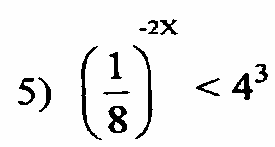
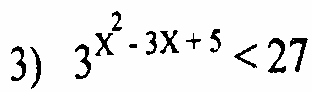
Найдите производную функци
1. 
2. 
3. 
4. 
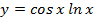
5. 
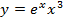
6. 
7. 
8. 
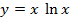
9. 
10. 
11. 
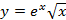
12. 
13. 
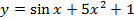
14. 
15. 
Найдите экстремумы функции
1. 
2.
3.
4.
ПРИМЕР ЭКЗАМЕНАЦИОННОГО БИЛЕТА
Министерство образования и науки Российской Федерации
ФГАОУ ВПО «Уральский федеральный университет
имени первого Президента России Б.Н.Ельцина»
Нижнетагильский технологический институт (филиал)
Нижнетагильский машиностроительный техникум
|
|
|
(факультет среднего профессионального образования)
| СОГЛАСОВАНО: Председатель ЦК ______________ (ФИО) Протокол № __ «__» ______ -___ 2011 г. | УТВЕРЖДАЮ: Заместитель директора техникума по УМР ____________ /Е.И. Гусева/ «___» _____________ 2011 г. |
Цикловая комиссия гуманитарных и общеобразовательных дисциплин
дисциплина: «Математика»
группы отделение очное
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 0
1. Решить уравнения:
a)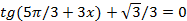 
b) 
2. Доказать тождества:
a) 
b) 
3. Решить уравнения:
a) 
b) 
4. Решить неравенства:
a) 
b)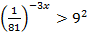 
5. Вычислить пределы функции:
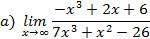
6. Найти производную функции:
a) 
b) найти производную и исследовать функцию на экстремум
|
|
|
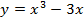
