Главная | Обратная связь | Поможем написать вашу работу!

V. Определение более правдоподобной гипотезы

Практическая часть

Откройте файл «Макет отчет_практика 3.docx», откройте исходные данные к заданию по варианту. Заполните шапку в отчете на странице 1.
Проанализировав проведенное исследование и его результаты, запишите ответы на вопросы в Задание 1.
Заполните Задания 2

I. Настройка программы LePAC

1) Запустите программу LePAC и нажмите RunLePac.

2) Выберете вкладку LeBayesiens – LesProportions: new window.

3) Переключите с 1 group на 2 independent groups (2 независимых группы).

4) Переключите с Pr(X<x) на Pr(x₁<X<x₂).

5) Далее изменяем значение с 0,95 на 0,99, так рассматриваться будут 99% доверительные интервалы (99% ДИ)

6) В окне Data - cell counts введите результат исследования.

II. Анализ для эффекта 1

1) Вычисляем долю для эффекта 1 в первой группе исследуемых. В правом части окна отметьте j1, нажмите кнопку Compute.

2) В таблицу Задание 2 запишите значение и 99 % доверительный интервал для j1 следующим образом:

Пример записи в шаблон: _0,807 0,83 _0,857

3) Далее в вопросе 1 приведите окно программы для расчет j1 и напишите по вашему исследованию смысл j1.

4) Аналогичным образом вычислите j2, заполните таблицу в задание 2 и ответьте на вопрос 2

Разность долей (RD)

1) Для вычисления первого показателя переключите на RD=j1-j2

2) Нажимаем Compute

3) Выписываем значение и 99% доверительный интервал для разности долей в таблицу.

4) Отвечаем на вопрос 3, приводя окно программы для расчета RD и описав смысл данного показателя.

5) Оценка разности долей: Когда доли равны, то их разность равна нулю (Можно провести аналогию с двумя одинаковыми числами: если два числа одинаковые – то разность этих чисел = 0). Если RD = φ 1 - φ 2 = 0, то доли в данном исследовании равны.

Будут ли они равны статистически? Нужно посмотреть, накрывает ли полученный 99%-й ДИ для разности долей значение RD = 0. Это дает нам основание утверждать, что, скорее всего, истинное (оцениваемое этим интервалом) значение RD статистически (на уровне значимости a = 0,01) отличается (если не накрывает 0) или не отличается (если накрывает 0) от значения «0» и что, соответственно, первая и вторая доли статистически не равны (если не накрывает 0) или равны(если накрывает 0).

Запишите полученные выводы в вопрос 4. При этом нужно оценить практическая важность разности долей по шкале. Сделайте также вывод: влияет ли наличие какого-либо признака на исход.

Отношение долей (RR)

1) Для вычисления второго показателя переключите на RR=j1/j2

2) Нажимаем Compute

3) Выписываем значение и 99% доверительный интервал для отношения долей в таблицу.

4) Отвечаем на вопрос 5, приводя окно программы для расчета RR и описав смысл данного показателя.

5) Оценка отношения долей: Когда доли равны, то их отношение равно единице. Если RR = φ1/φ2 = 1, то доли в данном исследовании равны.

Будут ли они равны статистически? Нужно посмотреть, накрывает ли полученный 99%-й ДИ для отношения долей значение RR = 1. Это дает нам основание утверждать, что, скорее всего, истинное (оцениваемое этим интервалом) значение RR статистически (на уровне значимости a = 0,01) отличается (если не накрывает 1) или не отличается (если накрывает 1) от значения «1» и что, соответственно, первая и вторая доли статистически не равны (если не накрывает 1) или равны (если накрывает 1).

Запишите полученные выводы в вопрос 6. При этом нужно оценить практическая важность отношения долей по шкале. Сделайте также вывод: влияет ли наличие какого-либо признака на исход.

Отношение шансов (OR)

1) Для вычисления следующего показателя переключите на w= [ φ ₁ / (1 - φ ₁)]: [ φ ₂ / (1 - φ ₂)]

2) Нажимаем Compute

3) Выписываем значение и 99% доверительный интервал для отношения шансов в таблицу.

4) Отвечаем на вопрос 7, приводя окно программы для расчета OR и описав смысл данного показателя.

5) Оценка отношения шансов:

Когда доли равны, то их отношение шансов единице. Если OR = [ φ ₁ / (1 - φ ₁)]: [ φ ₂ / (1 - φ ₂)] = 1, то доли в данном исследовании равны.

Будут ли они равны статистически? Нужно посмотреть, накрывает ли полученный 99%-й ДИ для отношения шансов значение OR = 1. Это дает нам основание утверждать, что, скорее всего, истинное (оцениваемое этим интервалом) значение OR статистически (на уровне значимости a = 0,01) отличается (если не накрывает 1) или не отличается (если накрывает 1) от значения «1» и что, соответственно, первая и вторая доли статистически не равны (если не накрывает 1) или равны (если накрывает 1).

Запишите полученные выводы в вопрос 8. При этом нужно оценить практическая важность отношения шансов по шкале. Сделайте также вывод: влияет ли наличие какого-либо признака на исход.

III. Анализ для эффекта 2

Расчет φ ₁, φ ₂, RD, RR, OR для второго эффекта производится, поменяв местами столбцы с помощью кнопки «1/0».

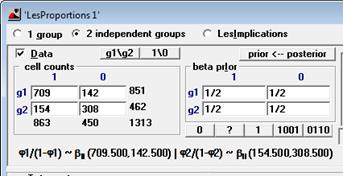
Заполните таблицу полностью и для эффекта 1 и для эффекта 2 (вопрос 9)

IV. Общий вывод

Сформулируйте общий вывод по задачи. Связаны ли показатель и рассматриваемые эффекты? Свои ответы запишите в отчет (вопрос 10)

V. Определение более правдоподобной гипотезы

Бейзов фактор – показатель того, насколько хорошо две гипотезы могут предсказать данные.

Гипотеза, которая предсказывает наблюдаемые данные лучше – это та из них, которая имеет больше свидетельств в свою пользу.

Бейзов фактор (BF) принципиально отличается от Р-значения. Бейзов фактор не является вероятностью сам по себе, а является отношением вероятностей, и он может варьировать от нуля до бесконечности.

Бейзов фактор требует две гипотезы, тем самым четко указывая, что если есть свидетельства против нулевой гипотезы, то должны существовать свидетельства и в пользу альтернативной гипотезы.

Но –нулевая гипотеза ( отсутствие различий между контрольной и опытной группой),

H₁ –альтернативная гипотеза ( наблюдаются различия между контрольной и опытной группой)

BF₀₁ = P(D|H₀)/ P(D|H₁)

BF₁₀ = P(D|H₁) / P(D|H₀)

В вербальных шкалах имеется словесная интерпретация Бейзова фактора:

1) Запустите приложение Exact BayesRxC.

2) Заносим исходные данные следующим образом: [[a11, a12],[a21, a22]]

Причем

Группа (выборка)	Эффект	Всего
Эффект 1	Эффект 2
Группа 1	a =a11	c =a12
Группа 2	b = a21	d =a22

3) Нажимаем: Rows are independent of columns

4) Выписываем значение БФ из открывшегося окна.

В Задание 3 для вопроса 1 приведите окно программы и запишите в явном виде значение Бейзова фактора.

Оценка BF₀₁:

1. BF₀₁>1 указывает, что более правдоподобна нулевая гипотеза

2. BF₀₁<1 указывает, что более правдоподобна альтернативная гипотеза

Воспользуйтесь поиском по сайту: