Решить задачи, используя информацию из вышеприведенного текста: (3 задачи – оценка «3», 4 задачи – оценка «4», 5-7 задач – оценка «5»)

Действительные и мнимые изображения.

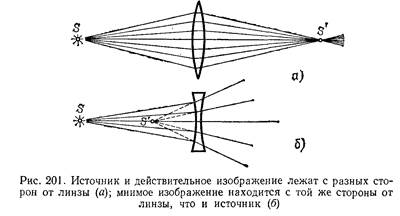Рассмотрим светящиеся точки (точечные источники света), находящих­ся на конечном расстоянии от линзы. Будем всегда считать источники расположенными слева от линзы. Что касается изображений, то в зависимости от вида линзы и положения источника относительно нее изображение S' может находиться как справа, так и слева от линзы. Если изображение лежит справа от линзы, то это означает, что оно образовано сходящимся пучком лучей (рис. 201, а), т. е. лучей, которые действительно проходят через точку S'. Изображение в этом случае называется действительным. Оно может быть получено на экране, фотопластинке и т. п. Восстановив ход лучей, приведших к образованию изоб­ражения, мы можем всегда найти местоположение источника, хотя практически это обычно связано с не­которыми трудностями. Предположим теперь, что изображение лежит слева от линзы, т. е. с той же стороны от нее, как и источник. Это означает, что пучок лучей, расходящихся от источника, после преломления в линзе становится еще более расходя­щимся, и в точке S' пересекаются лишь воображаемые про­должения преломленных лучей (рис. 201, б). Изобра­жение в этом случае называется мнимым. В действитель­ности ничего «мнимого» в этом случае, конечно, нет. Осо­бенностью мнимых изображений является то, что их нельзя получить непосредственно на экране, фотопластинке и т. п.

Преломление света

1. Абсолютный показатель преломления среды: n₁ = , где c – скорость света в вакууме, c1 – скорость света в среде.

2. Если свет идет из среды с абсолютным показателем преломления n₁ в среду с абсолютным показателем преломления n₂, то

n = = 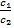- показатель преломления второй среды относительно первой.

3. Законы преломления:

1) Лучи, падающий и преломленный, и нормаль к границе раздела сред в точке падения лежат в одной плоскости.

2) Отношение синуса угла падения к синусу угла преломления равно относительному показателю преломления второй среды относительно первой: = n = , где α – угол между падающим лучом и нормалью, β – угол между преломленным лучом и нормалью.

Чем больше показатель преломления, тем среда оптически более плотная. Если свет идет из менее плотной в более плотную оптически среду, то α>β, если, наоборот, из более плотной в менее плотную, то α<β. В последнем случае возможен случай, β = 90°, при котором sin α₀ = . При α>α₀ луч полностью отражается от границы раздела сред; такое явление называется полным внутренним отражением.

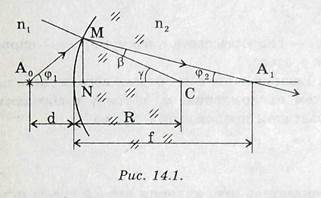
4. Сферическая поверхность, разделяющая две среды с показателями преломления n₁ и n₂, собирает узкий пучок лучей, идущий из точечного источника А₀ в первой среде, в точке А₁, являющейся изображением источника А₀ во второй среде. Формула такой оптической системы:

Обозначения понятны из рисунка. При этом d и f берутся со знаком «+» если точки А₀, А₁ – действительные, и со знаком «-» - если они мнимые; радиус R берется со знаком «+», если лучи, идущие от предмета, падают на выпуклую поверхность; со знаком «-» - если на вогнутую.

5. 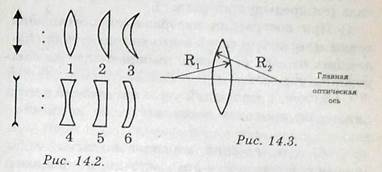Линза есть прозрачное тело, ограниченное криволинейными поверхностями. Простейшие линзы – сферические.

6. Свойства тонких линз.

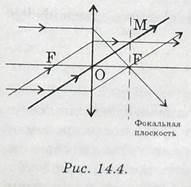
1) Параллельный пучок лучей после преломления в линзе собирается в одной точке, называемой фокусом (собирающие линзы). Геометрическое место фокусов есть плоскость, перпендикулярная оси линзы (фокальная плоскость) (рис. 14.4). Расстояние от фокальной плоскости до плоскости линзы есть фокусное расстояние F. Величина D = 1/F называется оптической силой линзы. Прямые, проходящие через оптический центр О линзы, называются оптическими осями.

2) Лучи, падающие на линзу параллельно какой-либо оптической оси, после преломления проходят через фокус, лежащий на этой оси.

3) Формула собирающей линзы: = + , f – расстояние от оси линзы до ее фокуса,

4) При построении изображения светящейся точки или предмета из всего потока лучей, падающих на линзу, обычно выбирают два из следующих четырех:

А) луч, проходящий через оптический центр линзы; он проходит через линзу, не преломляясь;

Б) луч, идущий параллельно какой-либо оптической оси; после преломления он проходит через фокус, лежащий на этой оптической оси;

В) луч, проходящий через передний фокус линзы, после преломления должен идти параллельно главной оптической оси;

Г) луч, проходящий через передний двойной фокус, после преломления пройдет через задний двойной фокус.

5) линейное увеличение предмета, даваемое собирающей линзой:

Г = = = 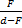, где H₀ - высота предмета, H – высота его изображения, d - расстояние от предмета до зеркала или линзы

7. Свойства тонких двояковыпуклых линз:

1) Параллельный пучок лучей после преломления в такой линзе расходится таким образом, что их продолжения пересекаются в одной точке – фокусе линзы. Геометрическое место фокусов есть плоскость, параллельная плоскости линзы. Все фокусы рассеивающей линзы мнимые.

2) Если лучи падают на такую линзу параллельно какой-либо оптической оси, то после преломления они выходят так, что их продолжения собираются в фокус, лежащий на этой оси.

3) Формулы рассеивающей линзы: - = 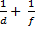; Г = = =

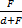
4) При построении изображений в рассеивающей линзе используют луч, идущий параллельно какой-либо оптической оси, и луч, идущий через оптический центр.

8. Если F - фокусное расстояние линзы, n_л – показатель преломления материала линзы, n _ср – показатель преломления среды, в которой находится линза, R₁ и R₂ – радиусы кривизны ограничивающих линзу поверхностей, то (*)

Радиус кривизны выпуклой поверхности следует брать со знаком «+», вогнутой – со знаком «-», для плоской поверхности R = ∞.

9. Увеличение оптических приборов: Г = ,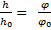

где h, h₀ – линейные размеры изображения на сетчатке вооруженного прибором глаза и без него; φ, φ₀ – углы, под которыми глаз видит предмет через прибор и без него.

Увеличение, даваемое микроскопом: Г =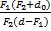

,где d – расстояние от предмета до объектива микроскопа; F₁ - фокусное расстояние объектива; F₂ – фокусное расстояние окуляра; d₀ – расстояние от мнимого изображения предмета до глаза наблюдателя. Расстояние L между окуляром и объективом (длина тубуса микроскопа):

L = +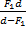

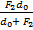
Если L, F₁ и F₂ известны, то (для нормального глаза) увеличение микроскопа: Г ≈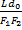

Алгоритмы решения типовых задач:

1. Задачи о преломлении света на границе раздела двух сред:

А) сделать чертеж, изобразив ход лучей, переходящих из одной среды в другую. В точке падения луча на границу раздела провести нормаль, отметить углы падения и преломления, учитывая при этом, в более или менее плотную среду переходит луч.

Б) записать закон преломления для каждого перехода луча из одной среды в другую, записать вспомогательные соотношения, связывающие углы и расстояния, исходя из геометрии задачи.

В) решить полученную систему уравнений и найти неизвестные величины.

2. Задачи на построение и расчет изображений в одиночных линзах:

А) сделать чертеж, отметив типичные точки линзы – фокус F и двойной фокус 2F? Расстояние от линзы до предметов.

Б) построить изображение предмета. Для этого удобнее брать характерные лучи: параллельные главной оптической оси и лучи, проходящие через оптический центр линзы.

Чтобы определить ход лучей из точек, расположенных на главной оптической оси, используются побочные оптические оси. Такую ось проводят через оптический центр линзы параллельно интересующему нас лучу и находят точку пересечения этой оси с фокальной плоскостью. Это и будет побочный фокус,в который и попадет после преломления пресловутый луч.

В) записав формулы фигурирующих в задаче линз и добавив к ним при необходимости формулу (*), решают полученную систему уравнений.

3. Оптические системы:

3.1 Оптические системы, состоящие из сложенных вплотную линз:

Сначала находят фокусное расстояние двух линз, сложенных вместе; если их фокусные расстояния равны F₁ и F₂, то фокусное расстояние такой системы F связано с ними формулой:

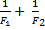= или D = D₁ + D₂ . Если F найдено, то дальнейшее решение задачи такое же, как и для одиночной линзы.

3.2 Оптические системы, состоящие из нескольких отстоящих друг от друга линз:

А) сделать рисунок, отметив линзы, их характерные точки, предмет и заданные расстояния.

Б) построить изображение предмета в первой линзе, игнорируя остальные.

В) используя формулу линзы и формулу увеличения (если необходимо), найти расстояние от изображения до первой и второй линз. При этом следует сразу же вычислять значения этих расстояний, что позволит судить о расположении этого изображения относительно второй линзы.

Г) считая первое изображение предметом для второй линзы, аналогичным образом находят положение и размер второго изображения. При необходимости процедура повторяется нужное число раз.

Если на вторую линзу лучи падают расходящимся пучком, то изображение точки нужно рассматривать как действительный предмет для второй линзы, а если на нее падает сходящийся пучок – то как мнимый предмет. Важен выбор знаков перед d и f. Если при составлении формул знаки были учтены, то при расчетах в полученные соотношения следует подставлять модули входящих в них величин.

3.3 Оптические системы, состоящие из линзы и зеркала:

В них преобразование света происходит трижды, причем независимо от того, состоят ли они из сложенных объектов или отстоящих друг от друга на некоторое расстояние. Ход лучей здесь таков: источник – линза -; преломление в ней – зеркало; отражение в нем – линза; повторное преломление – окончательное изображение. Изображение может быть действительным и мнимым. Порядок расчета в таких системах такой же, как и в системах, составленных из линз.

Отражение света

Световой луч — это бесконечно узкий пучок электромагнитных волн, совпадающий с направ­лением распространения световой волны. Свето­вая волна, падающая на границу раздела двух сред, частично отражается от нее, частично про­ходит во вторую среду.

Законы отражения света:

1. Угол падения а равен углу отражения р (углы отсчитываются от нормали к поверхности раздела сред в точке падения).

2. Падающий луч, отраженный луч и нормаль к поверхности в точке падения лежат в одной плоскости.

Если падающие на плоскую поверхность па­раллельные лучи после отражения от нее остаются параллельными, то та­кое отражение называется зеркальным, а отражаю­щая поверхность — пло­ским зеркалом.

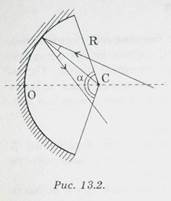На рисунке 13.1. луч 1 — падающий, 2 — отражен­ный, S' — мнимое изобра­жение точечного источни­ка S, п — нормаль к отра­жающей поверхности в точ­ке падения А.

Если отражающая поверхность представляет собой часть шаровой поверхности, то такое зер­кало называется сферическим (рис. 13.2.). Центр шара (точка С) называют оптическим центром зеркала, его радиус — радиусом зеркала. Верши­на шарового сегмента О называется по­люсом зеркала. Угол α — апертура зерка­ла. Прямая, проходящая через оптичес­кий центр и полюс зеркала, называется главной оптической осью. Всякая другая прямая, проходя­щая через оптичес­кий центр, называет­ся побочной оптичес­кой осью зеркала. Если на вогнутое зеркало падает параллельный пучок лучей, то после отражения вcе лучи пересекаются в одной точке, которая называется фокусом зеркала. Расстояние от фокуса до зерка­ла называется фокусным расстоянием.

Фокусное расстояние F зеркала радиуса R равно: F = R/2

Если светящаяся точка находится на расстоя­нии d от зеркала и ее изображение получается на расстоянии f от него, то: = = . Здесь F > 0 всегда для вогнутого зеркала, f > 0, d > 0 — если точки действительные, и f < 0, d < 0 — если точки мнимые.

Если l, l₀ — расстояния от изображения и предмета до фокуса зеркала, то формула зеркала такова: F² = = l₀l. (2)

Если предмет высотой H₀ расположен пер­пендикулярно главной оптической оси, а высота его изображения равна Н, то линейное увеличение (уменьшение предмета), даваемое зеркалом, равно: Г = = = 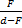(3)

Выпуклые сферические зеркала имеют сле­дующие свойства. Если на такое зеркало падает параллельный пучок лучей, то после отражения лучи расходятся и идут так, что их продолжения пересекаются в одной точке, называемой фоку­сом. Фокусы выпуклого зеркала мнимые.

Формула выпуклого зеркала: - = - = + (4)

Левая часть (4) всегда отрицательна. В правой части члены берутся со знаками «плюс» или «минус» в зависимости от того, являются изо­бражение или предмет действительными или мнимыми. Для выпуклого зеркала справедлива

формула (2).

Формула увеличения: Г = = =

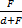
Алгоритмы решения типовых задач:

1.Задачи о плоском, вогнутом и выпуклом зеркалах.

а) Сделать чертеж, изобразив зеркало, его главную оптическую ось, фокус и центр, а так­же предмет, изображение которого требуется найти.

б) Построить изображение предмета. Для это­го обычно достаточно найти изображение двух его крайних точек. Изображение точек предме­та строят при помощи двух характерных лучей:

— луч, идущий от точки предмета параллель­но какой-либо оптической оси; после отражения он проходит через фокус, лежащий на этой оси;

— луч, проходящий через оптический центр зеркала; после отражения он идет по тому же на­правлению назад.

Ход отраженного луча, падающего под произ­вольным углом на сферическое зеркало, можно определить и с помощью побочной оптической оси. Для этого параллельно падающему лучу на­до начертить побочную оптическую ось, найти на ней побочный фокус (точку пересечения фокаль­ной поверхности с осью) и через него провести от­раженный луч.

в) Записать расчетные уравнения на основе формулы зеркала и формулы увеличения. Особое внимание следует уделить знакам перед d, f и F, о чем говорилось выше.

г) Решить полученные уравнения относитель­но искомой величины.

2. Задачи на построение и расчет систем зеркал. Здесь все расчеты и построения основывают­ся на том, что, в силу обратимости хода лучей, изображение, даваемое первым зеркалом, нужно рассматривать как предмет для второго, изображение, даваемое вторым, - как предмет для первого. Следует при этом учитывать, что промежуточный предмет – изображение для следующего зеркала – может быть как действительным, (в формулах d следует брать со знаком «+»), так и мнимым (d – со знаком «-»). В остальном задачи такого типа принципиально не отличаются от задач с одним зеркалом.

Решить задачи, используя информацию из вышеприведенного текста: (3 задачи – оценка «3», 4 задачи – оценка «4», 5-7 задач – оценка «5»)

1. Оптическая сила тонкой линзы 5 дптр. Предмет поместили на расстоянии 60 см от линзы. Где и какое изоб­ражение этого предмета получится?

2. Предмет помещен на расстоянии 25 см от перед­него фокуса собирающей линзы. Изображение предмета получается на расстоянии 36 см за задним фокусом. Опре­делите фокусное расстояние линзы.

3. Расстояние между стеной и свечой 2 и. Когда между ними поместили собирающую линзу на расстоянии 40 см от свечи, то на стене получилось четкое изображение пламени. Определите главное фокусное расстояние линзы. Какое изображение получилось на экране?

4. Главное фокусное расстояние рассеивающей лин­зы равно 12 см. Изображение предмета находится на рас­стоянии 9 см от линзы. Чему равно расстояние от предмета до линзы?

5. Предмет расположен на расстоянии 40 см от лин­зы с оптической силой 2 дптр. Как изменится расстояние до изображения предмета, если его придвинуть к линзе на 15 см?

6. Светящийся предмет находится на расстоянии 12,5 м от линзы, а его действительное изображение — на расстоянии 85 см от нее. Где получится изображение, если предмет придвинуть к линзе на 2,5 м?

7. Расстояние между предметом и экраном 120 см. Где нужно поместить собирающую линзу с фокусным рас­стоянием 25 см, чтобы на экране получилось четкое изображение предмета?

Поделиться:

Воспользуйтесь поиском по сайту: