Теперь научимся ее вычислять.

Лабораторная работа №1

Применение прикладной программы Microsoft Excel

К решению задач в социологии.

Содержание работы: На основе совокупности данных опыта необходимо выполнить следующее:

1. Построить ряд распределения и изобразить его графически (построить полигон, гистограмму, кумуляту).
2. Вычислить характеристики: моду, медиану, выборочную среднюю, выборочное среднее квадратичное отклонение, коэффициент вариации, асимметрию, эксцесс.

Пример. Пусть в результате анализа получены следующие значения цен на хлеб в городе Тюмени 9(в рублях).

13,21	14,51	12,01	13,42	13,61	14,02	12,12	13,22	13,66	13,43
13,88	13,32	13,82	13,49	12,48	13,26	13,58	13,81	13,84	13,31
13,55	12,32	12,38	13,24	13,46	13,73	14,18	13,70	13,45	13,23
13,41	13,52	13,58	12,87	13,01	13,30	13,36	14,45	14,13	13,53
13,53	12,78	13,59	13,54	14,21	13,41	12,42	13,47	13,30	14,37
13,13	13,67	13,25	13,48	13,25	12,59	14,15	13,44	12,30	13,22
13,50	14,26	12,60	13,27	13,29	13,35	12,96	13,51	13,55	13,50
12,61	12,90	14,27	12,88	13,33	13,57	13,38	13,56	13,40	13,10
13,40	13,93	13,16	13,34	13,00	12,72	13,12	13,39	13,19	13,99
13,18	13,28	13,80	13,39	13,78	13,85	13,90	13,94	13,27	14,79

Найдём X_min и X_max и округлим их (в меньшую и большую стороны соответственно).

Найдём R= X_max - X_min.

Возьмём l=7 и найдём h=R/l.

Xmax=	14,79	Округлим вверх	14,8
Xmin=	12,01	Округлим вниз	12,0
R=	2,8
L=
h=	0,4

Получим 7 частичных интервалов. Подсчитаем число значений признака(n_i), попавших в каждый частичный интервал (полученные результаты отобразить на Листе 2(Табл. А)(получим 7 таких таблиц)).

Таблица А

		12,01				12,12
	12,32	12,38
								12,3

Полученный результат отобразим в виде общей таблицы:

Таблица 1

Интервалы	12,0	12,4	12,8	13,2	13,6	14,0	14,4
12,4	12,8	13,2	13,6	14,0	14,4	14,8
ni

Полученный ряд называется интервальным вариационным рядом. Изобразим его графически.

Полученная ступенчатая фигура называется гистограммой распределения.

В качестве вариант x_i примем середины частичных интервалов.

Составим статистический ряд распределения (таблица 2).

Таблица 2

Xi	12,2	12,6		13,4	13,8	14,2	14,6
ni
wi	0,05	0,07	0,12	0,49	0,16	0,08	0,03
Wi	0,05	0,12	0,24	0,73	0,89	0,97

w_i =n_i/n

W_i = w_i – W_i-1

Построим точки с координатами (x_i;w_i) и соединим их – получим так называемый полигон относительных частот.

 

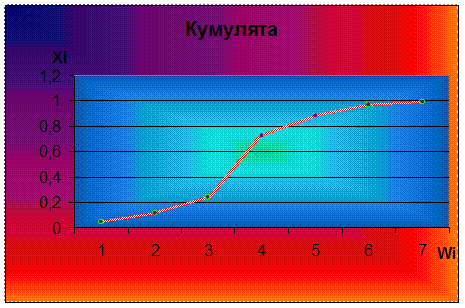
Построим точки с координатами (x_i;W_i) и соединим их – получим график, который называется кумулятой.

По выборке, используя данные табл. 2, находим точечные оценки параметров генеральной совокупности:

1. Моду – варианту, имеющую наибольшую частоту (Вставка-Функция-Статистические-Мода).

Mo=

13,22

1. Медиану – варианту, которая делит вариационный ряд на две части, равные по числу вариант (Вставка-Функция- Статистические-Медиана).

Me=

13,41

1. Выборочную среднюю, которая вычисляется по формуле:

1. Среднее квадратичное отклонение σ_в, которое вычисляется по формуле:

σ_в= , где

1. Коэффициент вариации

1. Асимметрию

Коэффициент асимметрии — это мера отклонения распределения частоты от симметричного распределения, то есть такого, у которого на одинаковом удалении от среднего значения по обе стороны выборки данных располагается одинаковое количество значений. Если наблюдения подчиняются нормальному распределению, то асимметрия равна нулю. Для проверки на нормальное распределение можно применять следующее правило: Если асимметрия значительно отличается от нуля, то гипотезу о том, что данные взяты из нормально распределенной генеральной совокупности, следует отвергнуть. Если вершина асимметричного распределения сдвинута к меньшим значениям, то говорят о положительной асимметрии, в противоположном случае — об отрицательной.

1. Эксцесс

(Коэффициент вариации или эксцесс): Коэффициент вариации указывает, является ли распределение пологим (при большом значении коэффициента) или крутым. Коэффициент вариации равен нулю, если наблюдения подчиняются нормальному распределению. Поэтому для проверки на нормальное распределение можно применять еще одно правило: Если коэффициент вариации значительно отличается от нуля, то гипотезу о том, что данные взяты из нормально распределенной генеральной совокупности, следует отвергнуть.

Для вычисления этих числовых характеристик составим расчётную таблицу.

Xi	ni	xi · ni	xi - xв	(xi - xв)·ni	(xi - xв)^2 ·ni	(xi - xв)^3 ·ni	(xi - xв)^4 ·ni
12,2		61,00	-1,20	-6,00	7,20	-8,64	10,37
12,6		88,20	-0,80	-5,60	4,48	-3,58	2,87
		156,00	-0,40	-4,80	1,92	-0,77	0,31
13,4		656,60	0,00	0,00	0,00	0,00	0,00
13,8		220,80	0,40	6,40	2,56	1,02	0,41
14,2		113,60	0,80	6,40	5,12	4,10	3,28
14,6		43,80	1,20	3,60	4,32	5,18	6,22
Σ				0,00	25,60	-2,69	23,45

Mo=	13,22
Me=	13,41
xв=	13,4
Dв=	0,256
σв	0,51
V=	3,78%
As=	-0,208
Ex=	0,58

УМЕЕТЕ ВЫЧИСЛЯТЬ ДИСПЕРСИЮ?

ТЕПЕРЬ НАУЧИМСЯ ЕЕ ВЫЧИСЛЯТЬ.

ДИСПЕРСИЯ (методичка → с 11).

Дисперсия — это квадрат стандартного отклонения и, следовательно, эта характеристика также является мерой разброса измеренных величин. Она определяется как сумма квадратов отклонений всех измеренных значений от их среднеарифметического значения, деленная на количество измерений минус 1.

 

Из математической статистики известно, что самой известной мерой разброса количественного признака является его дисперсия.

Поделиться:

Воспользуйтесь поиском по сайту: