Средняя кинетическая энергия поступательного движения молекулы идеального газа пропорциональна термодинамической температуре и зависит только от него.

Величина R/N_А = k в уравнении (31) получила название постоянной Больцмана и представляет собой газовую постоянную, отнесенную к одной молекуле:
k = 1,38·10^-23 Дж/К^-23.

Так как = kТ, то средняя квадратичная скорость равна

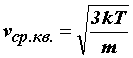. (32)

Подставляя значение средней кинетической энергии поступательного движения молекул в основное уравнение молекулярно–кинетической теории газов, получим другую форму уравнения состояния идеального газа:

P = n₀kT. (33)

Давление газа пропорционально произведению числа молекул в единице объема на его термодинамическую температуру. Среднеквадратичная скорость молекул равна квадратному корню из среднего квадрата скорости молекул:

(5)

Вычислим среднеквадратичную скорость из средней кинетической энергии молекул, которую мы легко можем сосчитать:

(6)

С учетом уравнения (4) получим:

(7)

 

Физический смысл постоянной Больцмана заключается в следующем:

постоянная k показывает, какая работа совершается каждой молекулой при

изобарическом расширении газа, при увеличении температуры на 1 градус

 

14.Теплоемкость газа при постоянном давлении и постоянном объеме. Формула Р. Майера.

 

Особый интерес представляют средние и истинные теплоемкости в процессах при постоянном объеме 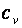(изохорная теплоемкость, равная отношению удельного количества теплоты в изохорном процессе к изменению температуры рабочего тела dT) и при постоянном давлении 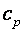(изобарная теплоемкость, равная отношению удельного количества теплоты в изобарном процессе к изменению температуры рабочего тела dT).

Для идеальных газов связь между изобарной и изохорной теплоёмкостями и устанавливается известным уравнением Майера .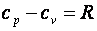

Из уравнения Майера следует, что изобарная теплоемкость больше изохорной на значение удельной характеристической постоянной идеального газа. Это объясняется тем, что в изохорном процессе () внешняя работа не выполняется и теплота расходуется только на изменение внутренней энергии рабочего тела, тогда как в изобарном процессе () теплота расходуется не только на изменение внутренней энергии рабочего тела, зависящей от его температуры, но и на совершение им внешней работы.

Для реальных газов 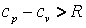, так как при их расширении и совершается работа не только против внешних сил, но и внутренняя работа против сил взаимодействия между молекулами газа, на что дополнительно расходуется теплота.

В теплотехнике широко применяется отношение теплоемкостей , которое носит название коэффициента Пуассона (показателя адиабаты).

 

Теплоемкост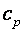и и 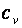зависят от температуры, следовательно, и показатель адиабаты должен зависеть от температуры.

Известно, что с повышением температуры теплоёмкость 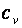увеличивается. Поэтому с ростом температуры уменьшается, приближаясь к единице. Однако всегда остается больше единицы. Обычно зависимость показателя адиабаты от температуры выражается формулой вида

,

где - значение коэффициента при 0⁰ С; - коэффициент, принимающий для каждого газа своё постоянное значение.

Кроме того, можно установить следующие широко использующиеся зависимости.

,

(2.8)

и так как

. .   (4.2.8) Это уравнение Майера для одного моля газа.

 

47.Движение заряженных частиц в магнитном поле. Сила Лоренца. Устройство и принцип действия осциллографа.

 

Если заряженная частица движется в магнитном поле со скоростью v, перпен­дикулярной вектору В, то сила Лоренца F = Q [ vB ] постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центро­стремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяется из условия QvB=mv²/r откуда Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,

Подставив сюда выражение, получим

т. е. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду (Q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v<<c). На этом основано действие циклических ускорителей заряженных частиц.

Если скорость v заряженной частицы направлена под углом альфа к вектору В,то ее движение можно представить в виде суперпозиции: 1) равномерного прямолиней­ного движения вдоль поля со скоростью v _|| =v cos ; 2) равномерного движения со скоростью v _= v sin бета по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется формулой (в данном случае надо заменить v на v _= v sin ). В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 170). Шаг винтовой линии

Подставив в последнее выражение (115.2), получим

Направление, в котором закручивается спираль, зависит от знака заряда частицы.

Если скорость v заряженной частицы составляет угол  с направлением векто­ра В неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то r и h уменьшаются с ростом В. На этом основана фокусировка заряженных частиц в магнитном поле.

Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью заряд лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического и магнитного полей. Выражается в СИ как:

 

Поделиться:

Воспользуйтесь поиском по сайту: