 |
На практике с помощью вольтметра измеряется напряжение Холла
|
|
|
|
Лабораторная работа № 7 ((ФПК))
ИЗУЧЕНИЕ ЭФФЕКТА ХОЛЛА в полупроводниках
Цель работы – исследование эффекта Холла в полупроводниковом датчике путем измерения ЭДС Холла при изменении направления и величины тока через датчик и направления и величины индукции магнитного поля.
Краткая теория
Эффектом Холла называется появление в проводнике с током плотностью 
, помещённом в магнитное поле 
, электрического поля 
, перпендикулярного и . При этом напряжённость электрического поля называют ещё полем Холла (рис.7.1).
 |
Эффект открыт Эдвином Гербертом Холлом в 1879 в тонких пластинках золота. Для наблюдения эффекта Холла вдоль прямоугольных пластин из исследуемых веществ, длина которых 
значительно больше ширины 
и толщины 
, пропускается ток:
. (7.1)
Сам проводник помещался в магнитное поле, индукция которого перпендикулярна направлению протекания электрического тока в проводнике.
На середине боковых граней, перпендикулярно току, расположены электроды, между которыми измеряется ЭДС Холла, равная
. (7.2)
Простейшая теория эффекта Холла объясняет появление ЭДС Холла взаимодействием носителей тока (электронов проводимости в металлах и полупроводниках, а также дырок в полупроводниках) с магнитным полем.
Под действием электрического поля носители заряда приобретают направленное движение (дрейф), средняя скорость которого (дрейфовая скорость) 
. Как известно, плотность тока в проводнике
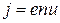, (7.3)
где 
— концентрация числа носителей, 
— их заряд. При наложении магнитного поля на носители действует сила Лоренца:
, (7.4)
под действием которой частицы отклоняются в направлении, перпендикулярном 
и . В результате на обеих гранях проводника конечных размеров происходит накопление заряда и возникает электростатическое поле — поле Холла. В свою очередь электрическое поле Холла действует на заряды с силой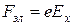 
и уравновешивает силу Лоренца. Возникает состояние динамического равновесия, при котором
|
|
|
. (7.5)
Найдем скорость направленного движения из формулы (7.3) и подставим в (7.5), сократив при этом величину :
. (7.6)
Величину 
принято обозначать 
(измеряется она в см3/Кл) и называть коэффициентом Холла (или постоянной Холла). Коэффициент Холла является основной характеристикой эффекта Холла. При этом напряженность поля Холла становится равной
. (7.7)
На практике с помощью вольтметра измеряется напряжение Холла
. (7.8)
Плотность тока выразим через силу тока 
, подставим в(7.8), получим
. (7.9)
Знак совпадает со знаком носителей тока. Для металлов, у которых концентрация носителей (электронов проводимости) близка к плотности атомов (»1023см-3),
~10-5(см3/Кл), у полупроводников концентрация носителей значительно меньше и ~105 (см3/Кл). Коэффициент Холла может быть выражен через подвижность носителей заряда 
и удельную электропроводность. Из закона Ома в дифференциальной форме 
. Подвижность носителей тока является важной характеристикой веществ, она численно равна средней скорости направленного движения, приобретаемой носителями тока при напряженности электрического поля, равной единице. Если в поле напряженности 
носители приобретают скорость 
, то их подвижность равна:
. (7.10)
Коэффициент Холла становится равным
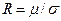. (7.11)
Коэффициент Холла (для изотропных полупроводников) выражается через парциальные проводимости электронов и дырок 
и 
и концентрацию электронов 
э и дырок 
:
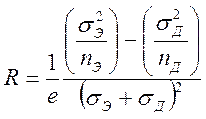(a) для слабых полей (7.12)
(б) для сильных полей.
В чистых (собственных) полупроводниках 
для всей области магнитных полей:
|
|
|
, (7.13)
а знак указывает на преобладающий тип проводимости.
Из формул видно, что знак постоянной Холла совпадает со знаком заряда частиц, обусловливающих проводимость данного материала. Поэтому на основании измерения постоянной Холла для полупроводника можно судить о природе его проводимости: если <0, то проводимость электронная, если >0, то дырочная. Если в полупроводнике одновременно осуществляются оба типа проводимости, то по знаку постоянной Холла можно судить о том, какой из них является преобладающим.
С помощью постоянной Холла можно также определить концентрацию носителей заряда, если характер проводимости и их заряд известны (например, для металлов) 
.
Так, для одновалентных металлов оказалось, что концентрация электронов проводимости совпадает с концентрацией атомов.
|
|
|
