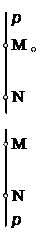|
Принадлежность точки, прямой и плоскости
|
|
|
|
ТЕТРАДЬ ДЛЯ РЕШЕНИЯ ЗАДАЧ
по дисциплине " Инженерная графика"
для студентов технологических специальностей
/ТТП, НТС/
СТУДЕНТ ____________________
ГРУППА ____________________
ПРЕПОДАВАТЕЛЬ ____________
ТВЕРЬ 2014
УДК 744 (075.8)
ББК 30.11.я7
Предназначена для студентов первого курса технологических специальностей. Содержит задачи по дисциплине " Инженерная графика".
 Обсуждена и рекомендована к печати на заседании кафедры «Инженерная графика» (протокол №2 от.10.09.2014 г).
Обсуждена и рекомендована к печати на заседании кафедры «Инженерная графика» (протокол №2 от.10.09.2014 г).
Составитель: Федоров Б.А.
ТЕТРАДЬ ДЛЯ РЕШЕНИЯ ЗАДАЧ
по дисциплине "Начертательная геометрия. Инженерная графика"
для студентов технологических специальностей
/ТТТ,,НТС/
Составитель: Федоров Б.А.
Редактор
Технический редактор
Подписано к печати
Формат 60х84 1/8 Бумага писчая
Печ.л. Усл.печ.л. Уч-изд.л.
 Тираж экз. Заказ № С –
Тираж экз. Заказ № С –
Тверь. Типография ТГТУ
ã Тверской государственный технический
университет, 2014
ОБЩИЕ УКАЗАНИЯ
Рабочая тетрадь содержит задачи, которые студент должен решить во время лабораторных занятий или в порядке домашних заданий по дисциплине "Начертательная геометрия. Инженерная графика".
Решение задач по теоретическим основам инженерной графики, способствует развитию навыков пространственного мышления, необходимых в инженерной практике.
Оформление решений задач должно соответствовать общим правилам государственных стандартов ЕСКД. Условие задачи и результат решения выполняют основной сплошной линией по ГОСТ 2.303–68. Линии связи, базы отсчета, простановка размеров и вспомогательные построения проводятся тонкой сплошной линией. Линии невидимого характера – штриховой линией.
|
|
|
Принятые обозначения
1. Точки – обозначаются прописными буквами латинского алфавита.A, B, C, D, E, F и т.д. или цифрами 1, 2, 3…
2. Прямые – обозначаются строчными буквами латинского алфавита. a, b, c, d, l и т.д.
3. Отрезок прямой заданный двумя точками, обозначается в соответствии с обозначением этих точек … AB, FE, MN, 1‑2, а его длина – |АВ|, |1-2|.
4. Плоскости – обозначаются прописными буквами греческого алфавита…Σ, Ω, Θ или буквами русского алфавита, изображение которых отличается от латинского. – Б, Г, Д, Ф и т.д.
5. Прямые и плоскости уровня:
h – горизонталь:
f – фронталь;
p – профильная прямая;
Г – горизонтальная плоскость;
Ф – фронтальная плоскость;
П – профильная плоскость.
6. Знаки: ≡ – совпадение (А ≡ В)
|| – параллельность (а || с)
∩ – пересечение (а ∩ Б)
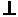 – перпендикулярность (n
– перпендикулярность (n 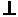 Б)
Б)
D – треугольник

 – скрещивание (ас)
– скрещивание (ас)

 – принадлежность (а Б)
– принадлежность (а Б)
□ – квадрат
= – равенство, решение (К = а ∩ Б)
1. Построение комплексного чертежа
Задача №1
 |
Построить комплексный чертеж точек: А(40,30,15), B(10,0,30), C(0,25,10),
Задача №2
 |
Достроить недостающий третий вид точек А, В и С
Задача №3
Построить вид слева (профильную проекцию) треугольной пирамиды.

Задача №4
Построить вид сверху DАВС.
 |
2. Прямые частного положения
Задача №5.
| Построить чертежи следующих прямых: | ||
| а) Горизонтали h, расположенной под углом 30° к фронтальной плоскости Ф. Отложите на ней отрезок длиной 40 мм; | б) Фронтали ¦, расположенной под углом 45° к горизонтальной плоскости Г. Отложите на ней торезок 30 мм; | в) Профильной прямой р, под углом 60° к фронтальной плоскости Ф. Отложите на ней отрезок 35 мм. |
| Задача №6 | ||
| Построить чертежи проецирующих прямых и отложить на них отрезок длиной 30мм: | ||
| а) i1 ^ плоскости Ф; | б) i2 ^ плоскости Г; | в) i3 ^ плоскости П; |
|
|
|
3. Плоскости частного положения
Задача №7.
Построить чертежи из трех видов:
| а) Равностороннего треугольника со стороной 30 мм, лежащего в горизонтальной плоскости. | б) Квадрата со стороной 35 мм, лежащего во фронтальной плоскости. | в) Прямоугольного треугольника с катетами 25 и 40 мм, принадлежащего профильной плоскости. |
Задача №8.
а) Через точку А провести горизонтально-проецирующую плоскость Б под углом 45° к фронтальной плоскости Ф и построить треугольник, принадлежащий этой плоскости;
б) Через точку В провести фронтально-проецирующую плоскость Д под углом 30° к горизонтальной плоскости Г и построить квадрат, принадлежащий этой плоскости.
а) б)
 | |||
 | |||
Задача №9.
 |
Плоскость D АВС – горизонтально-проецирующая. Достроить вид сверху (горизонтальную проекцию) треугольника.
Задача №10.
Определить, является ли DАВС проецирующей плоскостью?
 |
4.Прямые общего положения.
Определение натуры отрезка и углов его наклона (способ дополнительного вида)
| Задача №11. Построить чертеж восходящей прямой l, выбрать на ней произвольные точки А и В. Определить длину отрезка АВ и угол его наклона к горизонтальной плоскости. | Задача №12. Построить чертеж нисходящей прямой t, выбрать на ней произвольные точки С и D. Определить натуру отрезка CD и угол его наклона к фронтальной плоскости. | ||||||
Задача №13.
Построить вид сверху восходящего отрезка АВ, наклоненного к фронтальной плоскости под углом 30°.
| Задача №14.
Построить проекции отрезка АВ, принадлежащего m, если длина АВ=35мм.
| ||||||
Задача №15.
Разделить в отношении АС/CB=1/4 отрезок прямой общего положения.
| Задача №16.
Разделить точкой Е в отношении СЕ/ED=2/3 отрезок прямой профильного положения.
|
5.Плоскости общего положения.
Принадлежность точки, прямой и плоскости
Задача №17.
Построить чертежи:
а) Восходящей плоскости общего положения, заданной DАВС;
б) Нисходящей плоскости общего положения, заданной параллельными прямыми a||b.
 Задача №18.
Построить произвольные горизонталь, фронталь и профильную прямые в плоскости Б (АВС). Задача №18.
Построить произвольные горизонталь, фронталь и профильную прямые в плоскости Б (АВС).
| Задача №19.
Достроить вид спереди DАВС лежащего в плоскости Б(a||b).
 
| ||||||||
Задача №20.
Достроить вид сверху четырехугольника ABCD принадлежащего плоскости (hÇf).
| Задача №21.
Достроить плоский пятиугольник, провести в нем произвольные h и f.
|
5.2. Построение дополнительного вида плоскости
| Задача №22. Выполнить комплексные чертежи из 4-х изображений: | ||||
а) квадрата в горизонтально проецирующей плоскости Б, со стороной, равной 25 мм.
| б) треугольника со сторонами |АВ|=20мм, |ВС|=25мм, |АС|=30мм, лежащего во фронтально проецирующей плоскости Д с углом к горизонтальной плоскости равным 30о |
Задача №23
Определить натуральную величину DАВС.

6. Поверхности
Принадлежность точки, линии поверхности
Задача №24.
 Достроить линию MN, принадлежащую поверхности. Построить вид слева. Достроить линию MN, принадлежащую поверхности. Построить вид слева.
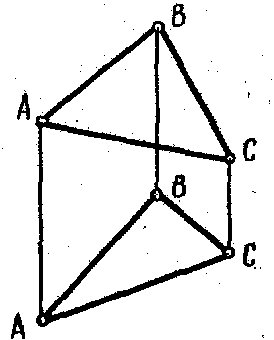
| Задача №25.
 Достроить линию АВС на поверхности конуса. Построить вид слева. Достроить линию АВС на поверхности конуса. Построить вид слева.
| ||
Задача №26. Достроить линию EFD принадлежащую поверхности сферы.
|
7. Аксонометрические проекции
| Задача №27 Построить прямоугольную изометрию точек: А/20,30,0/; В/35,15,20/; С/10,0,30/ | Задача №28
 Построить прямоугольную диметрию кривой DE. Построить прямоугольную диметрию кривой DE.
|
Задача №29
Построить прямоугольную диметрию усеченной пирамиды и линию АВ на ее поверхности.
 |
Задача №30
Построить прямоугольную изометрию призмы с отверстием.
 |
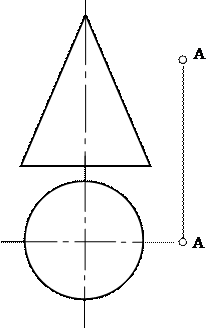
8.1. Взаимное расположение точек, точки и прямой, точки и плоскости
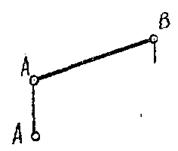
Задача №31.
Определить расположение точек B,C,D,E относительно точки А.

| Задача №32.
Построить точки:
а) т.А выше и правее т.М;
б) т.В левее и ближе т.М;
в) т.С ниже, правее и дальше т.М;
г) т.D дальше т.М
|
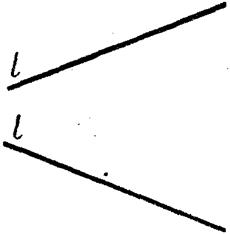
Задача №33.
Относительно прямой l построить точки:
а) т.А на прямой l;
б) т.В дальше прямой l;
в) т.С выше и ближе l;
г) т.D ниже прямой l.
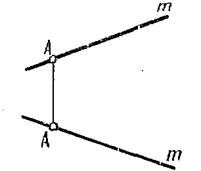
| Задача №34.
Относительно прямой р построить точки:
а) т.А на прямой р;
б) т.В дальше прямой р;
в) т.С выше и ближе р;
г) т.D ниже прямой р.
|
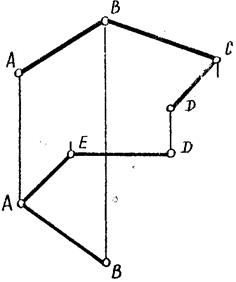
Задача №35.
Относительно плоскости Б(АВС) построить точки:
а) т.Е дальше пл.Б;
б) т.F ниже пл.Б;
в) Можно ли построить точку лежащую ближе и выше пл.Б?
| Задача №36.
Определить положение точек M и N относительно плоскости Д(а || b).
|
8.2. Взаимное расположение прямых, прямой и (плоскости и поверхности)
Задача №37.
Через т.А провести прямую параллельную:
а) прямой l

б) профильной прямой p.
Задача №38.
Через т.А провести горизонталь h и фронталь ¦:
а) пересекающие прямую l;

б) пересекающие профильную прямую p.
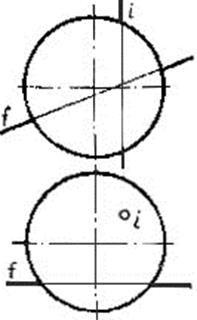
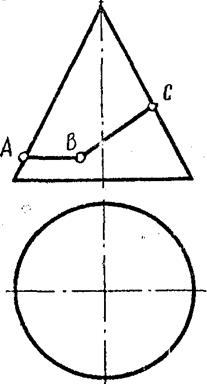
Задача №39.
Определить взаимное расположение прямых m и p.
| |||||||||||
Задача №40.
Определить взаимное расположение прямой и плоскости.
| |||||||||||
Задача №41.
 Через точку А провести прямую параллельную плоскости Д(aÇb). Через точку А провести прямую параллельную плоскости Д(aÇb).
| Задача №42.
 Через точку А провести прямую m параллельную плоскости Д(а || b) и горизонтальной плоскости. Через точку А провести прямую m параллельную плоскости Д(а || b) и горизонтальной плоскости.
| ||||||||||
Задача №43.
Определить точки пересечения прямой l с поверхностью призмы.

| Задача №44.
Определить точки пересечения прямой l и i c поверхностью треугольной пирамиды.

| ||
Задача №45.
Определить точки пересечения прямой h, l, i с поверхностью конуса. |
Задача №46.
Определить точки пересечения прямых со сферой.
| Задача №47.
 Определить точки пересечения прямой а со сферой. Определить точки пересечения прямой а со сферой.
|
8.3. Пересечение плоскостей, плоскости и поверхности
Задача №48.
Построить линию пересечения плоскостей.

| Задача №59.
Построить линию пересечения плоскостей.
 
| |||
Задача №50.
Через точку А провести плоскость параллельную заданной плоскости Б(а || b).

| ||||
Задача №51
Построить линию пересечения плоскости Б(а || b) с поверхностью призмы.
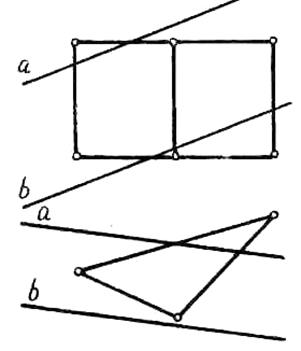
| Задача №52
Построить натуру сечения пирамиды плоскостью Д.

| |||
Задача №53
Построить натуральную величину сечения конуса:
 а) по эллипсу; в) по гиперболе.
а) по эллипсу; в) по гиперболе.

9. Развертки поверхностей.
Построить развертки поверхностей, нанести на них линию принадлежащую поверхности.

Задача №54
Задача №55

Задача №56
 |
10. Ортогональная проекция прямого угла.
Методы преобразования чертежа
(Способ замены плоскостей проекций)
Задача №57
Определить расстояние от т.А до:
а) Прямой уровня;
б) Прямой общего положения.
|
|
|
 |
а) б)
Задача №58
Определить расстояние от т.А до:
а) проецирующей плоскости Б (BCD);
б) плоскости общего положения Д (h ∩ f)
а) б)
 |
Задача №59
Определить величину угла между a и b:
а) пересекающимися
б) скрещивающимися
 |
a) б)
 |
Задача №60
 |
Определить величину угла между l и плоскостью Б (АВС).
Задача №61
|
|
 |  |
Определить расстояние между прямыми.
Методы преобразования чертежа
(Метод вращения вокруг проецирующей прямой)
Задача № 62. Определить расстояние от точки А до боковой поверхности прямого кругового конуса.
| Задача №63. Определить расстоя-
ние от точки А до поверхности
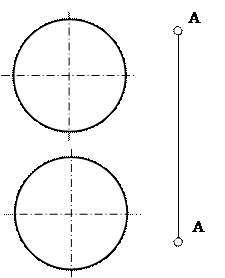 сферы. сферы.
|
Библиографический список
1. Посвянский А.Д. Краткий курс начертательной геометрии. - М.: Высшая школа, 1974.
2. ЕСКД. Общие правила выполнения чертежей. М.: Гос. комитет СССР по стандартам, 1984. –234с.
3. ГОСТ 2.305-68. Изображения – виды, разрезы, сечения.
4. ГОСТ 2.317-69. Аксонометрические проекции.
5. ГОСТ 2.303-68. Линии.
ТЕТРАДЬ ДЛЯ РЕШЕНИЯ ЗАДАЧ
по дисциплине "Инженерная графика"
для студентов технологических специальностей
/ТТП, НТС/
Составитель: Федоров Б.А.
Редактор
Технический редактор
Подписано к печати
Формат 60х84 1/8 Бумага писчая
Печ.л. Усл.печ.л. Уч-изд.л.
 Тираж экз. Заказ № С –
Тираж экз. Заказ № С –
Тверь. Типография ТГТУ
|
|
|