 |
Модели с конечной импульсной характеристикой
|
|
|
|
Специальность:09.02.01 «Компьютерные системы и комплексы»
КУРСОВАЯ РАБОТА
Дисциплина: «Цифровая схемотехника»
Тема: «Цифровое устройство «6-ти командная RC-цепь»
Выполнил: студент группы Э-2-15Вопиловский Т.И
Принял: Познахирко В.В.
Введение
o Немного вводных тем…1
o Пассивные элементы…1-2
o Резистор…2-4
o Конденсатор…4-5
o RC-цепь…5-7
o Дифференцирующая цепь…7-10
o Интегрирующая цепь…11-12
o Дискретная цепь…12-13
o Фильтр (и характеристики)…14(14-15)
o Характеристики амплитудных модификаций…16
o 6-командная RC-цепь…17
o Филтр Баттерворта…18
o Фильтр Чебышева…19
o Словарь терминов…20
o
Немного вводных тем
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 1 |
| КП 190702.12.000 ПЗ |
Ток (условное обозначение I). Ток – это скорость перемещения электрического заряда. Единицей измерения тока служит ампер. Обычно ток измеряют в амперах (А), миллиамперах (1 мА = 10-3А), микроамперах (1 мкА = 10-6А), наноамперах (1 нА=10-9А). Ток величиной 1А создается перемещением заряда в 1 кулон за время, равное 1 сек. Условились считать, что ток в цепи протекает от точки с более положительным потенциалом к точке с более отрицательным потенциалом, хотя электрон перемещается в противоположном направлении.
|
|
|
Напряжение всегда измеряется между двумя точками схемы, ток всегда протекает через точку в схеме или через какой-нибудь элемент схемы.
Законы Кирхгофа.
1. Сумма токов, втекающих в точку, равна сумме токов вытекающих из нее (сохранение заряда). В электронике эту точку схемы называют узлом. Из этого закона вытекает следствие: в последовательной цепи ток во всех точках одинаков.
2. При параллельном соединении элементов (рис.1) напряжение на каждом из элементов одинаково. Иначе говоря, сумма падений напряжения между точками А и В, измеренная по любой ветви схемы, соединяющей эти точки, одинакова и равна напряжению между точками А и В.
Рис.1 
Иногда это правило формулируется так: сумма падений напряжения в любом замкнутом контуре схемы равна нулю.
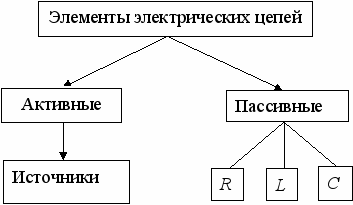
Пассивные элементы
Пассивные элементы электроники – это элементы способные только ослабить сигнал.
Пассивными элементами являются следующие:
- базовые ЭК, имеющиеся практически во всех электронных схемах радиоэлектронной аппаратуры (РЭА):
- сопротивления, реализованные в виде резисторов;
- ёмкости, реализованные в виде конденсаторов;
- ЭК, в которых используется явление электромагнитной индукции:
- трансформаторы;
- дроссели (катушки индуктивности);
- ЭК, построенные на базе электромагнитов:
- соленоиды;
- реле;
- пьезоэлектрические ЭК:
- кварцевый резонатор;
- линии задержки, применяемые в радиоэлектронике;
- всевозможные соединители и разъединители цепи — ключи, применяемые для создания электрических цепей;
- предохранители, применяемые для защиты цепей от перенапряжения и короткого замыкания;
- индикаторы, применяемые для создания световых сигналов;
- динамики (точнее, динамические головки громкоговорителей), применяемые для создания звуковых сигналов;
- микрофон и видеокамера, применяемые для формирования сигнала;
- антенны, применяемые для излучения или приёма радиоволн;
- аккумуляторы, применяемые для обеспечения работы устройств вне сети электрического тока.
|
|
|
Резистор
Падение напряжения на участке цепи прямо пропорционально току, протекающему через цепь и обратно пропорционально силе тока: 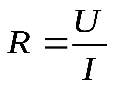 (закон Ома). Объекты, для которых выполняется закон Ома, называют резисторами. Однако, закон Ома выполняется не для всех элементов. Например, ток, протекающий через неоновую лампу, представляет собой нелинейную функцию от приложенного напряжения (он сохраняет нулевое значение до критического значения напряжения, а в критической тоске резко возрастает). То же самое можно сказать и о целой группе других элементов – диодах, транзисторах, лампах.
(закон Ома). Объекты, для которых выполняется закон Ома, называют резисторами. Однако, закон Ома выполняется не для всех элементов. Например, ток, протекающий через неоновую лампу, представляет собой нелинейную функцию от приложенного напряжения (он сохраняет нулевое значение до критического значения напряжения, а в критической тоске резко возрастает). То же самое можно сказать и о целой группе других элементов – диодах, транзисторах, лампах.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 2 |
| КП 190702.12.000 ПЗ |
Параметры резисторов:
1. номинальная величина сопротивления R(Ом, кОм, МОм, мОм);
2. допуск + DR(в %): для обычных резисторов - + 5%, + 10%, для прецинзионных - + 1%, + 0,01%;
3. номинальная мощность – это та мощность, которую резистор способен длительное время рассеивать в пространство без изменения своих свойств (типовые мощности: 0,0625Вт, 0,125Вт).
Последовательное и параллельное соединение резисторов. Из определения сопротивления следуют следующие выводы:
1. сопротивление двух последовательно соединенных резисторов (рис.2 а) равно: R=R1+R2. При последовательном соединении резисторов всегда получаем большее сопротивление, чем сопротивление отдельного резистора.
2. сопротивление двух параллельно соединенных резисторов (рис.2 б) равно  . При параллельном соединении резисторов всегда получаем меньшее сопротивление, чем соединение отдельных резисторов.
. При параллельном соединении резисторов всегда получаем меньшее сопротивление, чем соединение отдельных резисторов.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 3 |
| КП 190702.12.000 ПЗ |
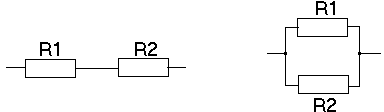
а) б)
Рис.2. Соединения резисторов.
Маркировка резисторов. Отечественная промышленность для маркировки резисторов использует надписи: Е – Ом, К- КОм, М – МОм. Например, надпись на резисторе 1К8 означает 1,8КОМ, К47 – 0,47КОм, 5М6 – 5,6МОм, 4Е7 – 4,7Ом.
|
|
|
Зарубежная промышленность пользуется цветной маркировкой. На резистор как правило наносится 5 цветных колец. В таблице № 1 представлена цветовая маркировка резисторов.
Табл.№1. Цветовая маркировка резисторов.
| цвет | Сопротивление | Допуск (5-я полоса) | |||
| 1-я цифра (1-я полоса) | 2-я цифра (2-я полоса) | 3-я цифра (3-я полоса) | Множитель (4-я полоса) | ||
| серебристый | 10-2 | + 10% | |||
| золотистый | 10-1 | + 5% | |||
| черный | |||||
| коричневый | + 1% | ||||
| красный | 102 | + 2% | |||
| оранжевый | 103 | ||||
| желтый | 104 | ||||
| зеленый | 105 | + 0,5% | |||
| голубой | 106 | + 0,25% | |||
| фиолетовый | 107 | + 0,1% | |||
| серый | 108 | + 0,05% | |||
| белый | 109 |
Номинальное сопротивление резистора выбирается не произвольно, а из стандартного ряда (таблица 2).
Таблица №2.
| Обозначение рядов | Обозначение рядов | ||||
| Е24 (допуск + 5%) | Е12 (допуск + 10%) | Е6 (допуск + 20%) | Е24 (допуск + 5%) | Е12 (допуск + 10%) | Е6 (допуск + 20%) |
| 1,0 | 1,0 | 1,0 | 3,3 | 3,3 | 3,3 |
| 1,1 | 3,6 | ||||
| 1,2 | 1,2 | 3,9 | 3,9 | ||
| 1,3 | 4,3 | ||||
| 1,5 | 1,5 | 1,5 | 4,7 | 4,7 | 4,7 |
| 1,6 | 5,1 | ||||
| 1,8 | 1,8 | 5,6 | 5,6 | ||
| 20, | 6,8 | 6,8 | 6,8 | ||
| 2,2 | 2,2 | 2,2 | 7,5 | ||
| 2,4 | 8,2 | 8,2 | |||
| 2,7 | 2,7 | 9,1 | |||
| 3,0 |
Конденсатор
Конденсатор – это устройство, имеющее два вывода и обладающее свойством, согласно которому заряд накопленный этим устройством прямо- пропорционален напряжению между выводами, а коэффициент пропорциональности называют емкостью конденсатора (Q=CU).
Конденсатор, имеющий емкость С фарад, к которому приложено напряжение U вольт, накапливает заряд Q кулон на одной пластине и –Q– на другой.
Продифференцировав выражение для Q, получим 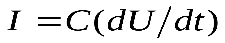 . Из этого выражения следует вывод, что конденсатор – это более сложный элемент, чем резистор; ток пропорционален не просто напряжению: а скорости изменения напряжения. Если напряжение на конденсаторе, имеющем емкость 1Ф, изменится на 1В за 1сек, то получим ток 1А. И наоборот, протекание тока 1А через конденсатор емкостью 1Ф вызывает изменение напряжения на 1В за 1сек. Емкость, равная 1Ф, очень велика, и поэтому чаще имеют дело с микрофарадами (мкФ) или пикофарадами (пФ).
. Из этого выражения следует вывод, что конденсатор – это более сложный элемент, чем резистор; ток пропорционален не просто напряжению: а скорости изменения напряжения. Если напряжение на конденсаторе, имеющем емкость 1Ф, изменится на 1В за 1сек, то получим ток 1А. И наоборот, протекание тока 1А через конденсатор емкостью 1Ф вызывает изменение напряжения на 1В за 1сек. Емкость, равная 1Ф, очень велика, и поэтому чаще имеют дело с микрофарадами (мкФ) или пикофарадами (пФ).
|
|
|
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 4 |
| КП 190702.12.000 ПЗ |
1. номинальная емкость;
2. максимальное напряжение – это напряжение, которое длительное время может быть приложено к конденсатору и не вызывать каких-либо изменений его свойств.
3. отклонения конденсатора + DС (допуск)
Последовательное и параллельное соединение конденсаторов. Емкость несколько параллельно соединенных конденсаторов равна сумме его емкостей. Нетрудно в этом убедиться: приложим напряжение к параллельному соединению, тогда
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 5 |
| КП 190702.12.000 ПЗ |
CU = Q =Q1 +Q2 +Q3+ … = C1U + C2U +C3U +… = (C1 +C2 +C3 + …)U или С = С1 +С2 +С3 +….
Для последовательного соединения конденсаторов имеем такое же выражение, как для параллельного соединения резисторов: 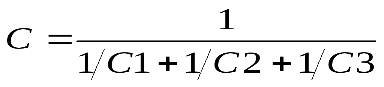 .
.
В частном случае для двух конденсаторов:  .
.
Номинальное значение, так же как и резистора выбирается из стандартного ряда (таблица 3). Стандартная величина емкости определяется по формуле С =a* 10n,n=0,1,2,3,… Значения коэффициентов приведены в таблице 3.
Таблица №3.
| Обозначение рядов | Обозначение рядов | ||||
| Е24 (допуск + 5%) | Е12 (допуск + 10%) | Е6 (допуск + 20%) | Е24 (допуск + 5%) | Е12 (допуск + 10%) | Е6 (допуск + 20%) |
| 1,0 | 1,0 | 1,0 | 3,3 | 3,3 | 3,3 |
| 1,1 | 3,6 | ||||
| 1,2 | 1,2 | 3,9 | 3,9 | ||
| 1,3 | 4,3 | ||||
| 1,5 | 1,5 | 1,5 | 4,7 | 4,7 | 4,7 |
| 1,6 | 5,1 | ||||
| 1,8 | 1,8 | 5,6 | 5,6 | ||
| 20, | 6,8 | 6,8 | 6,8 | ||
| 2,2 | 2,2 | 2,2 | 7,5 | ||
| 2,4 | 8,2 | 8,2 | |||
| 2,7 | 2,7 | 9,1 | |||
| 3,0 |
RC-цепь
RC-цепь — электрическая цепь, состоящая из конденсатора и резистора. Её можно рассматривать как делитель напряжения с одним из плеч, обладающих ёмкостным сопротивлением переменному току.
RC- цепи: изменения во времени напряжения и тока. Для анализа цепей переменного тока (или в общем случае схем, работающих с изменяющимися напряжениями и токами) можно использовать характеристики двух типов. Во-первых, можно рассматривать изменения напряжения U и тока I во времени, а во-вторых, - изменение амплитуды при изменении частоты сигнала. И те, и другие характеристики имеют свои преимущества, и в каждом практическом случае приходится выбирать наиболее подходящие.
|
|
|
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 6 |
| КП 190702.12.000 ПЗ |

Рис.3. RC- цепь. Рис.4. Сигнал разряда RC- цепи.
Воспользуемся полученным ранее выражением для емкости: 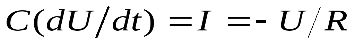 . Это выражение представляет собой дифференциальное уравнение, решение которого имеет вид
. Это выражение представляет собой дифференциальное уравнение, решение которого имеет вид  e-t/RC. Отсюда следует, что если заряженный конденсатор подключить к резистору, то он будет разряжаться так, как показано на рис.4.
e-t/RC. Отсюда следует, что если заряженный конденсатор подключить к резистору, то он будет разряжаться так, как показано на рис.4.
Постоянная времени.
Произведение RC называют постоянной времени цепи. Если R измерять в омах, в фарадах, то произведение RC будет измеряться в секундах. Для конденсатора емкость 1мкФ, подключенного к резистору сопротивлением 1кОм, постоянная времени составляет 1мс. Если конденсатор был предварительно заряжен и напряжение на нем составляет 1В, то при подключении резистора в цепи появится ток, равный 1мА.

Рис.5. RC- цепь. Рис.6.
На рис.5 показана несколько иная схема. В момент времени t=0 схема подключается к батарее. Уравнение, описывающее работу такой схемы, выглядит следующим образом: I =C(dU/dt) =(Uвх – Uвых)/ R и имеет решение Uвых = Uвх + Ae-t/RC. Постоянная величина А определяется из начальных условий (рис.6): U =0 при t =0, откуда A =-Uвх и Uвых =Uвх (1 – e-t/RC).
Установление равновесия. При условии t>>RC напряжение достигает значения Uвх (правило пяти: за время равное пяти постоянным времени, конденсатор разряжается или заряжается на 99%). Если затем изменить входное напряжение Uвх (сделать его, например, равным нулю), то напряжение на конденсаторе U будет убывать, стремясь к новому значению по экспоненциальному закону e-t /RC. Например, если на вход подать прямоугольный сигнал Uвх, то сигнал на выходе Uвых будет иметь форму, показанную на рис.7.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 7 |
| КП 190702.12.000 ПЗ |

Рис.7. Напряжение, снимаемое с конденсатора
(верхние сигналы), при условии, что на него через
резистор подается прямоугольный импульс.
Здесь возникает вопрос: каков закон изменения для произвольного Uвх(t)? Для того чтобы ответить на него, нужно решить неоднородное дифференциальное уравнение. В результате получим:
 Uвхt e – (t-t ) / RCdt.
Uвхt e – (t-t ) / RCdt.
Согласно полученному выражению, RC- цепь усредняет входное напряжение с коэффициентом пропорциональности e- Dt / RC, где Dt = t -t.
Дифференцирующая цепь
Дифференцирующие цепи. Имеется схема, изображенная на рис.8. Напряжение на конденсаторе С равно Uвх –Uвых, поэтому I = Cd(Uвх -Uвых)/dt = Uвых/R.
Довольно часто в электронике вообще, а в импульсной в частности требуется преобразовать один вид импульсов в другой (например, прямоугольный преобразовать в треугольный). Для этой цели используют различные схемы, в основе которых простейшие RC- и RL-цепи. Такие цепи называются дифференцирующими и интернирующими цепями. Для начала рассмотрим дифференцирующие цепи, которые показаны на изображении ниже.
Своё название дифференцирующие цепи получили от того, что напряжение на выходе такой цепи пропорционально производной входного напряжения, а нахождение производной в математике называется дифференцирование. В случае RC-цепи напряжение снимается с резистора, а в случае RL-цепи – с индуктивности.
 .
.
В настоящее время большинство дифференцирующих цепей основаны на RC-цепях, поэтому стоит рассмотреть их, но все основные выкладки соответствуют также и RL-цепям.
Можно рассмотреть, как дифференцирующая цепь будет реагировать на прямоугольный импульс. Прямоугольный импульс представляет собой как бы два скачка напряжения. Реакцию RC-цепи на скачкообразное изменение напряжения рассматривалась выше, а в случае прямоугольного импульса выходное напряжение с дифференцирующей цепи будет в виде двух коротких импульсов различной полярности, длительность которых соответствует 3τ = 3RC и 3τ = 3L/R, в случае RL-цепи.
Напряжение на выходе дифференцирующей цепи:
u вых = u вх – u c = u вх – u вх · (1 – e – t/τ) = u вх · e – t/τ);
Таким образом, по мере заряда конденсатора напряжение на выходе схемы убывает по экспоненциальному закону. Когда конденсатор полностью зарядится, напряжение на выходе дифференцирующей цепи станет равным нулю.
В момент окончания прямоугольного импульса напряжение на входе схемы скачком уменьшится до нуля. Поскольку конденсатор в это время остается полностью заряженным, то с этого момента начнется его разряд через сопротивление R. В начале разряда конденсатора напряжение на выходе схемы по величине приблизительно равно напряжению на конденсаторе, но с противоположным знаком, т. к. направление тока разряда противоположно току заряда. По мере разряда конденсатора напряжение на выходе цепи уменьшается по экспоненциальному закону.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 8 |
| КП 190702.12.000 ПЗ |
(Следующая страница)

| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 9 |
| КП 190702.12.000 ПЗ |
Из величины и формы выходного напряжения можно сделать вывод, что дифференциальные цепи вполне могут применяться для уменьшения длительности импульсов, что довольно часто применяется на практике и ранее такие цепи иногда называли укорачивающими.

Рис.8. Дифференцирующая RC- цепь.
Если резистор и конденсатор выбрать так, чтобы сопротивление Rи емкость C были достаточно малыми и выполнялось условие dUвых /dt << dUвх/dt, то
C(dUвх/dt) = Uвых/R или Uвых(t) = RC [dUвх(t)/dt].
Таким образом, получилось, что выходное напряжение пропорционально скорости изменения входного сигнала.
Для того, чтобы выполнялось условие dUвых/dt << dUвх/dt, произведениеRC должно быть небольшим, но при этом сопротивление R не должно быть слишком малым, чтобы не «нагружать» выход (при скачке напряжения на входе изменение напряжения на конденсаторе равно нулю и R представляет собой нагрузку со стороны выхода схемы). Если на вход схемы подать прямоугольный сигнал, то сигнал на выходе будет иметь вид, представленный на рис.9.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 10 |
| КП 190702.12.000 ПЗ |
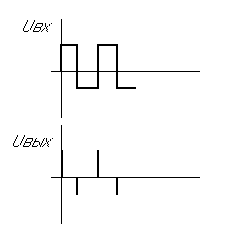
Рис.9. Входной и выходной сигналы
дифференцирующей RC- цепи.
Дифференцирующие цепи удобно использовать для выделения переднего и заднего фронтов импульсных сигналов. В цифровых схемах можно иногда встретить цепи, подобные той, которая показана на рис.10.
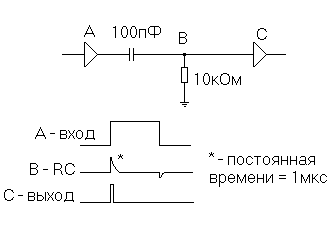
Рис.10. Выделение переднего фронта импульса.
Дифференцирующая RC- цепь генерирует импульсы в виде коротких пиков в моменты переключения входного сигнала, а выходной буферный усилитель преобразует эти импульсы в короткие прямоугольные импульсы. В реальных схемах отрицательный пик бывает небольшим благодаря встроенному в буфер диоду.
Интегрирующая цепь
Интегрирующие цепи. Рассматривается схема, изображенную на рис.11. Напряжение на резисторе R равно Uвх –Uвых, следовательно I = C(dU/dt) =(Uвх - Uвых)/R. Если обеспечить выполнение условия Uвых << Uвх за счет большего значения произведения RC, то получится С(dUвых/dt) 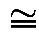 Uвх/R или Uвых(t) =
Uвх/R или Uвых(t) = 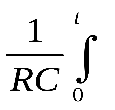 Uвх(t)dt + const.
Uвх(t)dt + const.
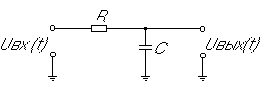
Рис.11. Интегрирующая RC- цепь.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 11 |
| КП 190702.12.000 ПЗ |
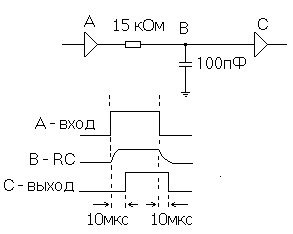
Рис.12. Использование RC- цепи для формирования
задержанного цифрового сигнала.
Отмечено, что условие Uвых <<Uвх равносильно тому, что ток пропорционален напряжениюUвх. Если бы в качестве входного сигнала выступал бы токI(t), а не напряжение, то получился бы идеальный интегратор. Источником тока может служить резистор с большим сопротивлением и с большим падением напряжения на нем, и на практике часто пользуются этим приближением.
Интегрирующие цепи находят широкое применение в аналоговой технике. Их используют в управляющих системах, схемах с обратной связью, при аналогово-цифровом преобразовании и генерации колебаний.
Дискретная цепь
Дискретной цепью называют любое устройство, которое преобразует входную последовательность отсчетов сигнала x (k) в выходную y (k). Пример подобного устройства приведен на рисунке 1.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 12 |
| КП 190702.12.000 ПЗ |

Рисунок 1. Пример изображения дискретной цепи
Обычно всех интересуют линейные дискретные цепи. Особенностью этих дискретных цепей является то, что на выходе не образуется новых частотных составляющих сигнала. Если дискретная цепь является фильтром, то соотношение частотных компонент спектра входного сигнала на выходе изменяется. Это удается сделать при помощи дискретной свертки сигнала. Формула дискретной свертки входной последовательности отсчетов с импульсной характеристикой дискретной цепи (фильтра) записывается следующим образом:
 (1)
(1)
где h (k) — импульсная характеристика дискретной цепи. Импульсную характеристику можно определить как отклик дискретной цепи на воздействие единичного импульса (δ-функция). Формулу свертки (1) можно записать в сокращенном виде, используя символ операции свертки '*':
y (k) = x (k)*h(k) (2).
Линейная дискретная цепь, будет устойчива, если выполняется условие
 (3)
(3)
Можно рассмотреть простейшую дискретную цепь. Для этого можно воспользоваться аналогиями между аналоговыми дискретными цепями. Одной из простейших аналоговых цепей является интегрирующая RC-цепочка. Принципиальная схема интегрирующей RC-цепочки приведена на рисунке 2.
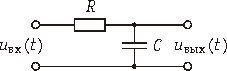
Рисунок 2. Принципиальная схема интегрирующей RC-цепочки
Импульсная характеристика интегрирующей RC-цепочки жестко связана с её амплитудно-частотной характеристикой. Зная импульсную характеристику любой схемы (цепи) можно узнать ее АЧХ, выполнив прямое преобразование Фурье над импульсной характеристикой. Если у двух разных схем будет одна и та же импульсная характеристика, то можно утверждать, что и амлитудно-частотные характеристики этих схем (цепей) будут одинаковыми. На рисунке 3 приведен пример импульсной характеристики интегрирующей цепочки.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 13 |
| КП 190702.12.000 ПЗ |
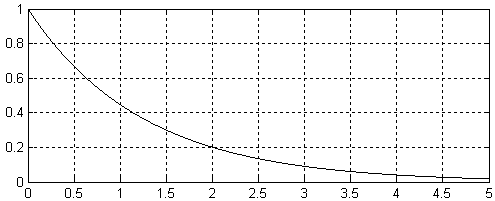
Рисунок 3. Импульсная характеристика интегрирующей RC-цепочки
Применения
§ Нелинейный интегратор
§ Фильтр нижних частот
§ Линии задержки сигналов
§ Формирование кратковременного уровня логического 0 или логической 1 для начальной установки состояния узлов цифровой техники (триггеров, счётчиков и т.д) при включении питания.

Рисунок 4. Структурная схема рекурсивной дискретной цепи
В схеме дискретной цепи, приведенной на рисунке 4, параллельный регистр RG выполняет функцию элемента задержки, который обычно обозначается Z−1. В данной схеме для вычисления очередного выходного отсчета сигнала используется следующая формула:
y (k) = x (k) + α·y (k −1) (4)
где α — коэффициент рекурсии.
Фильтр
Фильтр — понятия, устройства, механизмы, выделяющие (или удаляющие) из исходного объекта некоторую часть с заданными свойствами.
Цифровой фильтр — в электронике любой фильтр, обрабатывающий цифровой сигнал с целью выделения и/или подавления определённых частот этого сигнала. В отличие от цифрового, аналоговый фильтр имеет дело с аналоговым сигналом, его свойства недискретны, соответственно передаточная функция зависит от внутренних свойств составляющих его элементов.
Существуют различные типы цифровых фильтров, и в первую очередь разделение осуществляется по проводимости моделей. Устройства с параметром менее 5 мк не подходят для выделения высоких частот. Чувствительность у них колеблется в районе 40 мВ. Многие модификации используются в бытовой технике. Устройства с проводимостью более 5 мк подходят для трансформаторов. Еще есть модели с конечными и бесконечными импульсными характеристиками. В отдельную категорию выделены аппаратные, и программные фильтры.
Модели с конечной импульсной характеристикой
Устройства с конечной импульсной характеристикой выделяются низкой проводимостью. Для серверных приборов они не подходят. Также стоит отметить, что в устройствах низкая чувствительность. Как устроен фильтр? Резисторы у него используются контактного типа. На конце имеется три выхода. Непосредственно изолятор устанавливается с обкладкой. Многие модификации выпускаются без тетродов. Роль стабилизатора у них играет простой преобразователь. Показатель перегрузки модификаций зависит в первую очередь от модулятора, который находится рядом с резисторами. В среднем он составляет 4 А. Подключение фильтра к плате осуществляется через выходы, которые припаиваются к усилителю.
|
|
|


