 |
Дифференциальные уравнения первого порядка
|
|
|
|
Основные понятия и определения
В математике и ее приложениях часто возникает задача отыскания неизвестной функции. Один из основных приемов решения такой задачи – составление уравнения относительно этой функции. Во многих случаях эти уравнения содержат не только саму искомую функцию, но и ее производные или дифференциалы. Такого рода уравнения называют дифференциальными уравнениями.
Пример.
Тело массы т падает вертикально вниз с некоторой высоты. Требуется установить зависимость скорости падения от времени, если на тело, кроме силы тяжести, действует сила сопротивления воздуха (тормозящая сила), пропорциональная величине скорости.
Решение
Пусть 
– скорость тела в момент времени t. На тело действуют две противоположно направленные силы: сила тяжести 
и сила трения 
, где 
– коэффициент трения. Таким образом, в направлении движения на тело действует сила
.
С другой стороны, в силу второго закона Ньютона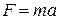 
, где а – ускорение, поэтому получаем
.
Используя равенство 
, имеем 
. Разделив обе части этого равенства на т, получим дифференциальное уравнение
.
Таким образом, исходная задача свелась к чисто математической задаче:
«Найти функцию 
, которая является решением уравнения 
, содержащего неизвестную функцию V и её производную 
».
Определение 23.1 Дифференциальным уравнением называется уравнение, связывающее независимые переменные, искомую функцию, и её производные (или дифференциалы) различных порядков. Порядок старшей производной неизвестной функции, входящей в данное дифференциальное уравнение, называется порядком этого уравнения.
Если неизвестная функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным. Если неизвестная функция есть функция нескольких переменных, и дифференциальное уравнение содержит частные производные этой функции, то его называют уравнением в частных производных.
|
|
|
Например,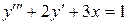 
– обыкновенное дифференциальное уравнение третьего порядка относительно неизвестной функции 
, а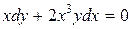 
– обыкновенное дифференциальное уравнение первого порядка. Причем последнее уравнение можно рассматривать как уравнение относительно функции , так и относительно функции 
. Уравнения
и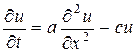 
есть дифференциальные уравнения второго порядка в частных производных относительно функции 
.
В дальнейшем будем рассматривать только обыкновенные дифференциальные уравнения.
В общем виде обыкновенное дифференциальное уравнение п -го порядка можно представить в виде
,
где х – независимая переменная, у = – неизвестная функция, а F – заданная функция своих аргументов. Если это уравнение можно записать в виде
,
то говорят, что оно разрешено относительно старшей производной или записано в нормальной форме.
Определение 23.2 Решением дифференциального уравнения п -го порядка называется всякая функция 
, 
, определенная и непрерывная вместе со своими производными до п -го порядка включительно, которая, при подстановке её в дифференциальное уравнение вместо неизвестной, обращает это уравнение в тождество.
Например, функци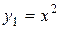и 
и 
являются решениями уравнения
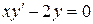
для любого х. Действительно, поскольку 
, то, подставляя и в уравнение, получим 
, 
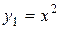. Аналогично имеем 
, 
. 
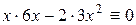Функции 
и 
есть решения уравнения
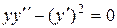
(проверьте самостоятельно!).
Операция отыскания всех решений дифференциального уравнения в некоторой области изменения независимой переменной называется интегрированием дифференциального уравнения.
График решения заданного дифференциального уравнения называется интегральной кривой этого уравнения.
|
|
|
Например, функция 
является решением дифференциального уравнения 
для всех 
. Действительно,
, 
,
следовательно, 
. График этой функции – гипербола (рисунок 1.1) и каждая из ветвей этой гиперболы является интегральной кривой данного дифференциального уравнения.
Основная задача теории дифференциальных уравнений состоит в нахождении всех решений заданного уравнения и изучении их свойств.
Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка имеет вид
.
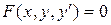Будем рассматривать только такие дифференциальные уравнения, которые можно записать в нормальной форме
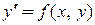. (1.1)
Часто используется также следующая форма записи дифференциального уравнения первого порядка:
. (1.2)
Указанные формы записи уравнений первого порядка тождественны в том смысле, что от одной из них с помощью тождественных преобразований и замены 
на 
(или наоборот) можно перейти к другой. Однако, если равенство (1.1) есть дифференциальное уравнение относительно функции 
, то равенство (1.2) можно рассматривать как уравнение относительно функции , так и как уравнение относительно функции 
.
Рассмотрим простейшее дифференциальное уравнение первого порядка
.
Нахождение решений этого дифференциального уравнения составляет знакомую нам основную задачу интегрального исчисления – отыскание первообразных функции 
. Значит, искомое решение имеет вид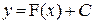 
, где F(x) – одна из первообразных функции , а С – произвольная постоянная. Следовательно, рассматриваемое нами простейшее дифференциальное уравнение имеет бесчисленное множество решений. Естественно, возникает вопрос: всякое ли дифференциальное уравнение в случае его разрешимости имеет бесконечное множество решений?
В то же время, при решении прикладных задач, приводящих к дифференциальным уравнениям относительно некоторой функции 
, по понятным соображениям требуется найти не все множество решений этого дифференциального уравнения, а только одно, удовлетворяющее определенным требованиям. В этом случае на искомую функцию накладывают дополнительные условия. Для дифференциального уравнения первого порядка эти условия чаще всего записывают в виде:
|
|
|
при 
, или 
, или 
. (1.3)
и называют начальными условиями, а величины у 0 и х 0 при этом называются начальными значениями.
Если дифференциальное уравнение описывает некоторый реальный процесс (физический, химический, природный, социальный и т.д.), то начальные условия (1.3), чаще всего, определяют начальное состояние этого процесса.
Определение 23.3 Задача отыскания решения дифференциального уравнения 
, удовлетворяющего начальным условиям , называется задачей Коши.
Геометрически задача Коши состоит в отыскании той интегральной кривой, которая проходит через заданную точку 
.
В связи с этим, возникает еще один вопрос: для любых ли начальных условий задача Коши разрешима и сколько она имеет решений?
Справедлива следующая теорема существования и единственности решения задачи Коши для дифференциального уравнения первого порядка.
Теорема 23.1 (Коши).
Если в дифференциальном уравнении функция 
и её частная производная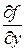 
непрерывны в некоторой области DÌR2, то для любой внутренней точки 
области D существует и притом единственное решение 
этого дифференциального уравнения, определенное в некоторой окрестности точки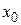 
и удовлетворяющее начальному условию 
.
Геометрический смысл теоремы Коши состоит в следующем: через каждую точку области D, в которой выполнены условия теоремы, проходит единственная интегральная кривая заданного дифференциального уравнения.
Таким образом, теорема Коши отвечает на оба поставленных нами вопроса:
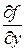1. В области D непрерывности функции и ее производной дифференциальное уравнение имеет бесконечное множество решений, каждое из которых соответствует определенному начальному условию . Геометрически эти решения образуют семейство интегральных кривых.
2. Для любого начального условия , ÎD, задача Коши разрешима и имеет единственное решение.
Таким образом, по виду правой части уравнения и по начальным данным можно определить, существует ли искомое решение задачи Коши для этого дифференциального уравнения и единственно ли оно.
Пусть D – область плоскости О ху, в которой выполнены условия теоремы Коши.
|
|
|
Определение 23.4 Общим решением дифференциального уравнения в области D называется функция 
, зависящая от произвольной постоянной С,непрерывно дифференцируемая по переменной х и удовлетворяющая условиям:
1) является решением этого дифференциального уравнения для любого значения С;
2) для всякого начального условия , 
, существует константа С 0 такая, что решение 
удовлетворяет этому начальному условию.
Общее решение, записанное в неявном виде Ф(х, у, С) = 0, называют общим интегралом дифференциального уравнения.
Геометрически общее решение определяет в области D семейство интегральных кривых.
Определение 23.5 Частным решением дифференциального уравнения в области D называется функция , которая получается из общего решения данного дифференциального уравнения при конкретном значении константы С = С 0.
Геометрически частное решение определяет одну кривую семейства интегральных кривых. Таким образом, задача Коши – это задача отыскания частного решения заданного дифференциального уравнения, удовлетворяющего заданным начальным условиям.
Если известно общее решение данного дифференциального уравнения, то чтобы найти его частное решение, удовлетворяющее начальному условию , используют следующий алгоритм:
1. В равенстве заменяют х на х 0, у на у 0.
2. Решают полученное уравнение у 0 = j(х 0, С) относительно С.
3. Подставляют найденное значение 
в общее решение вместо постоянной С.
4. Полученная функция и есть искомое частное решение.
Заметим, что теорема Коши гарантирует единственность решения только для точек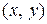 
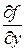, в которых функция и ее производной непрерывны. Если в некоторой точке (х 1, у 1) хотя бы одно из этих условий нарушается, то через эту точку может проходить несколько, или не проходить ни одной интегральной кривой дифференциального уравнения . Рассмотрим, например, уравнение 
. Функция 
и её частная производная 
не определены в точках 
, т.е. в точках оси О у. Общее решение этого дифференциального уравнения имеет вид 
. Геометрически уравнение определяет семейство парабол с вершинами в точке 
. Очевидно, через точку проходит бесконечное множество кривых этого семейства (интегральных кривых данного дифференциального уравнения), а через другие точки оси О у не проходит ни одной интегральной кривой.
Определение 23.6 Точки (х 0, у 0), в окрестности которых решение дифференциального уравнения, удовлетворяющее условию не существует, или существует, но не единственно, называются особыми точками.
Очевидно, для уравнения особыми являются точки, в которых либо функция , либо ее производная 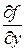имеют разрыв. Для рассмотренного выше уравнения особыми являются точки оси О у.
|
|
|
Может случиться и так, что дифференциальное уравнение имеет решение, которое ни при каких значениях константы С из общего решения не получается.
Например, для уравнения 
при у ³ 0 общее решение имеет вид 
. Но этому дифференциальному уравнению удовлетворяет, очевидно, и функция 
, которая не получается из общего решения ни при каком значении постоянной С. Нетрудно убедиться в том, что прямая
в каждой своей точке касается одной из интегральных кривых . Кроме того, во всех точках этой прямой производная 
функции 
имеет разрыв второго рода, т.е. все точки
этой прямой – особые.
Решение дифференциального уравнения, график которого состоит сплошь из особых точек, называют особым решением, а соответствующую интегральную кривую называют особой кривой данного дифференциального уравнения. Особое решение не может быть получено из общего решения дифференциального уравнения ни при каком значении постоянной С.
В общем случае, решить дифференциальное уравнение – значит найти все его решения, т.е. общее решение (общий интеграл) и особые решения, если они существуют. В данном пособии мы будем рассматривать только вопрос нахождения общего решения дифференциальных уравнений.
1.3 Геометрическая и механическая интерпретация дифференциального уравнения первого порядка
Пусть 
– решение дифференциального уравнения . По определению, эта функция имеет производную в каждой точке некоторого интервала 
. Значит, график этой функции есть кривая, в каждой точке которой можно провести касательную. Угловой коэффициент k касательной (тангенс угла её наклона к оси О х) в каждой точке кривой равен
, и значит, k = f (x, у).
Следовательно, дифференциальное уравнение устанавливает зависимость между координатами точки 
интегральной кривой и угловым коэффициентом касательной к интегральной кривой в этой точке.
Если в каждой точке М 
вычислить значение 
, то получим так называемое поле направлений касательных к интегральным кривым*) дифференциального уравнения.
Если для наглядности через каждую точку провести отрезок прямой (для определенности единичной длины) с серединой в этой точке и угловым коэффициентом, равным 
, то получим множество отрезков, каждый из которых является участком касательной к интегральной кривой, проходящей через точку 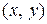. Совокупность этих отрезков дает геометрическую картину поля направлений заданного дифференциального уравнения и позволяет составить представление о поведении интегральных кривых в области D.
Таким образом, дифференциальное уравнение первого порядка определяет поле направлений, а каждое его решение определяет кривую в этом поле, направление касательной к которой в каждой точке совпадает с направлением поля в этой точке.
В связи с этим, задача интегрирования дифференциального уравнения , с геометрической точки зрения, может быть истолкована так: найти такую кривую, для которой касательная в каждой её точке имеет направление, совпадающее с направлением поля в этой точке.
|
Значит, построив поле направлений заданного дифференциального уравнения первого порядка, можно построить интегральные кривые этого уравнения.
Рассмотрим метод построения интегральных кривых, называемый методом изоклин.
Определение 23.8. Изоклиной *) дифференциального уравнения называется линия, в каждой точке которой направление (наклон) поля заданного дифференциального уравнения одно и то же, т.е. выполняется соотношение 
.
Из определения следует, что уравнение изоклины, соответствующей значению 
, имеет вид f (x, у) = k. Например, для дифференциального уравнения у¢ = х 2 + у 2 уравнения изоклин имеют вид х 2 + у 2 = k, очевидно это есть окружности радиуса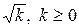 
.
Смысл параметра в следующем: k = tga, где a – угол, образованный касательной к интегральной кривой с положительным направлением оси О х.
Алгоритм метода изоклин включает следующие шаги:
1) Записать уравнения изоклин f (x, у) = k.
2) Построить изоклины, придавая k числовые значения из области значений функции .
3) Построить поле направлений. С этой целью для каждой изоклины найти угол a наклона поля направлений из условия 
и построить серию отрезков, пересекающих изоклину и проходящих под углом a к оси О х.
4) В полученном поле направлений построить искомые интегральные кривые так, чтобы они пересекали каждую изоклину под тем углом a, который указан на этой изоклине.
Замечание 1.
При построении изоклин выделяют изоклины нулей (
), на которых находятся точки экстремумов искомых интегральных кривых, и изоклины бесконечностей (
), в точках которых интегральные кривые имеют вертикальные касательные.
Замечание 2.
Чтобы получить достаточно точное представление о поведении интегральных кривых, нужно построить как можно более «густое» семейство изоклин. Если требуется решить дифференциальное уравнение с начальными условиями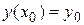 
, то строим одну интегральную кривую, проходящую через заданную точку 
.
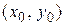Замечание 3.
Построить отрезок под углом a к оси О х, для которого 
, очень легко на клетчатой бумаге, используя известный факт: в прямоугольном треугольнике АВС с острым углом a 
есть отношение противолежащего катета ВС к прилежащему катету АВ.
Поэтому, если построить треугольник с катетами т и п, где 
, параллельными осям координат, а катет длины п параллелен оси О х, то гипотенуза этого треугольника будет наклонена к оси О х под углом a.
Исходя из этого, поле направлений можно построить так. Взять любую расположенную вблизи изоклины вершину клетки, пусть это точка А (рисунок 1.3). Из этой точки переместиться по горизонтали на п клеточек вправо, если 
> 0, или влево, если < 0 (точка В на рисунке 1.3). Из полученной точки В переместиться по вертикали на т клеток и соединить (хотя бы мысленно) вновь полученную точку С с исходной А. Тогда гипотенуза АС полученного треугольника укажет требуемый наклон поля. Затем проводим серию отрезков, пересекающих изоклину и параллельных АС.
 |
5). Полагая k = 0, ±1, ±2,..., ¥, построить изоклины f (x, у) = k, отмечая отрезком на каждой из них соответствующий наклон поля, например
k = 0, k = 1, k = –1, k = 2, k = –2,...., k = ¥ |.
Пример. Найти интегральную кривую ДУ у ¢ = 1 + у 2, проходящую через точку (0, 1).
Решение. Уравнение изоклин данного ДУ 1 + у 2 = k, или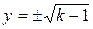 
. Будем придавать k значения (k ³ 1) и на соответствующих изоклинах отмечать отрезки, наклоненные под углом a таким, что tga = k. Для этого составим таблицу:
Чтобы построить искомую интегральную кривую, проведем через точку (0; 1) линию так, чтобы она пересекала каждую изоклину с таким наклоном, который указан на этой изоклине (рисунок 1.4).
О методе изоклин построения интегральных кривых можно прочитать также в [1], гл. 13, § 3.
Рассмотрим задачу о движении материальной точки по прямой, считая, что скорость движения зависит от времени и положения точки на прямой. Введем на плоскости декартову прямоугольную систему координат t O y. Прямую, по которой движется точка, примем за ось О у, другую ось координат будем считать осью времени t (рисунок 1.5). Тогда скорость движения v в общем случае есть функция 
времени t и положения y точки Р на оси О у. Требуется найти закон движения этой точки, т.е. зависимость 
.
Учитывая физический смысл производной: 
, из равенства 
получаем уравнение
.
Это дифференциальное уравнение первого порядка называют дифференциальным уравнением движения.
Всякое решение 
этого уравнения представляет собой некоторый закон (уравнение) движения точки по оси О у, его принято называть просто движением, определяемым данным дифференциальным уравнением. График функции –интегральная кривая – представляет собой график движения (не путайте с траекторией движения, которая есть отрезок оси О у, рисунок 1.6)
Задача Коши: 
, 
, состоит в нахождении такого движения , при котором движущаяся точка в момент времени t 0 находится в положении у 0 на оси О у.
Таким образом, с физической точки зрения, дифференциальное уравнение первого порядка есть дифференциальное уравнение движения точки по прямой; решение этого уравнения есть закон движения этой точки, интегральная кривая – график движения.
*) Если в каждой точке области Q задано значение некоторой величины, то говорят что в области Q задано поле этой величины.
*) изоклина– линия равного наклона
|
|
|
