 |
Промежутки возрастания или убывания функции
|
|
|
|
Функция: основные определения и понятия
Слово «функция» в переводе с латинского – исполнение действия.
Определение: Пусть  и
и  – непустые числовые множества, а х и у их элементы:
– непустые числовые множества, а х и у их элементы:  .
.
Если каждому элементу х из множества  ставится в соответствие только одно значение у из множества
ставится в соответствие только одно значение у из множества  , то говорят, что между переменными х и у существует функциональная зависимость
, то говорят, что между переменными х и у существует функциональная зависимость  .
.
Переменная х называется аргументом функции; переменная у - значением функции.
Свойства функции
Свойства функции мы будем рассматривать для прямоугольной системы координат хОу.
Самостоятельная работа с графиком функции выполняется в процессе лекции. Каждому учащемуся выдаётся произвольный график функции, для которого нужно записать все рассматриваемые свойства.
Область определения и область значения функции
Множество  называется областью определения функции (ООФ).
называется областью определения функции (ООФ).
В ООФ указывают промежуток (интервал) значений х существования функции.
Множество  называется областью значений функции (ОЗФ).
называется областью значений функции (ОЗФ).
В ОЗФ указывают промежуток (интервал) значений у существования функции.
Например:

| График схематичный. Функция графика задана формулой 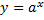 и поэтому можно сказать, что если и поэтому можно сказать, что если 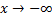 , то , то  ; если ; если 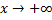 , то и , то и  .
Поэтому:
ООФ: .
Поэтому:
ООФ:  ОЗФ:
ОЗФ: 
|

| Если система координат оцифрована, то можно указать точные координаты начальной и конечной точек графика.
Поэтому:
ООФ:  ОЗФ:
ОЗФ: 
|

| Если график функции имеет разрыв, то ООФ и ОЗФ сообщают, не обращая внимание на разрыв функции.
Поэтому:
ООФ:  ОЗФ:
ОЗФ: 
|
Чётность и нечётность функции



| Функция  называется чётной, если для любого х существует значение –х, такое, что называется чётной, если для любого х существует значение –х, такое, что  .
График чётной функции симметричен относительно оси ординат (ось Оу).
Примеры чётных функций: .
График чётной функции симметричен относительно оси ординат (ось Оу).
Примеры чётных функций:  Функция
Функция  называется нечётной, если для любого х существует значение –х, такое, что называется нечётной, если для любого х существует значение –х, такое, что  .
График нечётной функции симметричен относительно начала координат (точки О).
Примеры нечётных функций: .
График нечётной функции симметричен относительно начала координат (точки О).
Примеры нечётных функций:  Большинство функций не являются чётными или нечётными.
График не имеет какую-либо симметрию.
Примеры таких функций:
Большинство функций не являются чётными или нечётными.
График не имеет какую-либо симметрию.
Примеры таких функций: 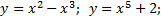
|
Периодичность функции
|
|
|
Функция называется периодичной, если существует такое число  что для любого х выполняется равенство
что для любого х выполняется равенство 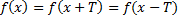 . Число Т называется периодом функции.
. Число Т называется периодом функции.
Примеры периодических функций: 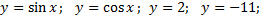

| 
|
Период этой функции 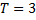
| Период этой функции 
|
Нули функции
Нулём функции называется такое действительное число х, при котором значение функции равно нулю.

| На графике нули функции – это точки пересечения графика с осью абсцисс (ось Ох), так как именно в этих точках 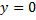 .
На данном графике нули функции это точки на оси Ох: .
На данном графике нули функции это точки на оси Ох: 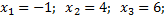
|
Промежутки знакопостоянства
Числовые промежутки, на которых непрерывная функция сохраняет свой знак и не обращается в нуль, называются промежутками знакопостоянства.
Определение знака функции:
- выше оси Ох - функция положительная  ;
;
- ниже оси Ох - функция отрицательная 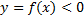
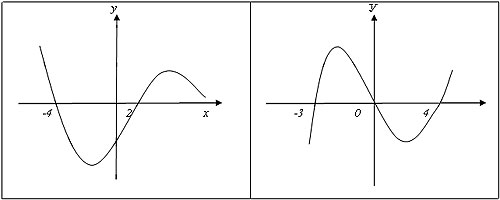
Например, для данных функций указать промежутки знакопостоянства:

| 
| 
|
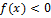 при при 
|  при при 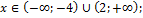
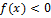 при при 
|  при при 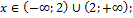
|
Монотонность функции


| Функция называется возрастающей, если с увеличением аргумента функции х, значения функции у так же увеличиваются.
Т.е. если  – функция возрастающая
Функция называется убывающей, если с увеличением аргумента функции х, значения функции у наоборот уменьшаются.
Т.е. если – функция возрастающая
Функция называется убывающей, если с увеличением аргумента функции х, значения функции у наоборот уменьшаются.
Т.е. если 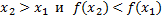 – функция убывающая. – функция убывающая.
|
 
| Монотонная функция — это функция, которая всё время либо возрастает, либо убывает.
Например:
Монотонно возраствющая функция  (рис.1)
Монотонно убывающая функция (рис.1)
Монотонно убывающая функция  (рис.2) (рис.2)
|
|
|
|
Промежутки возрастания или убывания функции

| Есть функции, которые многократно возрастают и убывают. В таких случаях указывают промежутки возрастания и убывания (это интервалы значений х).
Например, для данного графика есть два промежутка возрастания и два промежутка убывания:

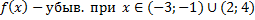
|
Экстремумы функции
Экстремумы функции – это общий термин для точек максимума и минимума функции.


| Функция  имеет минимум в точке имеет минимум в точке  , если существует такая окрестность точки , если существует такая окрестность точки  , что для всех других точек этой окрестности значение функции больше, чем в этой точке.
Для , что для всех других точек этой окрестности значение функции больше, чем в этой точке.
Для  если если  Функция
Функция  имеет максимум в точке имеет максимум в точке  , если существует такая окрестность точки , если существует такая окрестность точки  , что для всех других точек этой окрестности значение функции меньше, чем в этой точке.
Для , что для всех других точек этой окрестности значение функции меньше, чем в этой точке.
Для  если если 
|
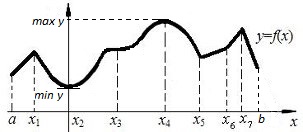
| Максимумы и минимумы функции не являются обязательно наибольшими и наименьшими значениями этой функции во всей области определения.
Например, на отрезке  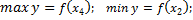
|
Непрерывность функции
Функция называется непрерывной на промежутке, если она определена на этом промежутке и непрерывна в каждой его точке.
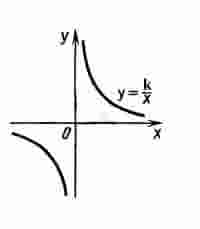
Например, для функции  точка
точка 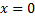 является точкой разрыва т.к. на нуль делить нельзя.
является точкой разрыва т.к. на нуль делить нельзя.
 
|  
|
| Непрерывные функции | Разрывные функции |
Пример выполнения задания по графику «Свойства функции»

| 1. Области определения и значения
ООФ:  ОЗФ:
ОЗФ:  .
2. Чётность и нечётность функции .
2. Чётность и нечётность функции
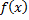 не является чётной. или нечётной.
3. Периодичность функции не является чётной. или нечётной.
3. Периодичность функции
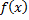 не периодичная.
4. Нули функции не периодичная.
4. Нули функции
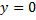 при при  5. Промежутки знакопостоянства
5. Промежутки знакопостоянства
 при при 
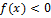 при при  6. Монотонность функции
6. Монотонность функции
 не монотонная. не монотонная.
 при при 
 при при 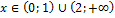 7. Экстремумы функции
7. Экстремумы функции

 8. Непрерывность функции
8. Непрерывность функции
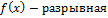 ; ;
 не существует на промежутке не существует на промежутке  и при и при  . .
|
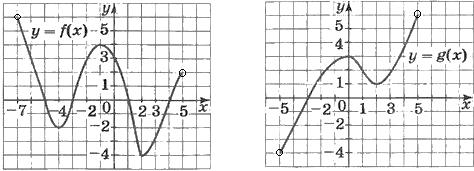
Самостоятельная работа
Выбрать график, перечертить его в тетрадь.
Для выбранного графика указать все рассмотренные свойства (св. 1 – 8).

|

|

|
|
|
|
|


