Задача №2.Расчёт политропного процесса сжатия газовой смеси в компрессоре.

Задача №1. Расчёт газовой смеси.

Газовая смесь состоит из нескольких компонентов, содержание которых в смеси задано в процентах по объёму: СО₂ = 18%; CО = 10%; N₂ = 72%.

Определить: 1)кажущуюся молекулярную массу смеси; 2) газовую постоянную смеси; 3) средние мольную, объёмную и массовую теплоёмкости смеси при постоянном давлении в пределах температур от t₁ = 126⁰C до t₂ = 528⁰C.

Решение:

1.Кажущаяся молекулярная масса смеси.

μ_СМ = ∑(r_i * μ_i),

где μ_i - молекулярная масса компонентов смеси;

r_i - объёмные доли компонентов смеси.

μ_СМ = r(СО₂)*μ(СО₂) + r(CO)*μ(CO) + r (N₂)*μ(N₂) = 0,18*44 + 0,10*28 + +0,72*28= 30,88.

2.Газовая постоянная смеси.

R_СМ = R / μ_СМ,

где R = 8314 Дж/(кг*К) – универсальная газовая постоянная.

R_СМ = 8314 / 30,88 = 269 Дж/(кг*К).

3.Перевод объёмных долей в массовые.

g_i = r_i * μ_i / (∑(r_i * μ_i),

g(CО₂) = r (СО₂)*μ(СО₂) /[r(СО₂)*μ(СО₂) + r(CO)*μ(CO) + r (N₂)*μ(N₂)]= =0,18*44/30,88 = 0,257;

g(CO) = r(CO)*μ(CO) /[r(СО₂)*μ(СО₂) + r(CO)*μ(CO) + r (N₂)*μ(N₂)] = =0,10*28/30,88 = 0,091;

g(N₂) = r (N₂)*μ(N₂)/[r(СО₂)*μ(СО₂) + r(CO)*μ(CO) + r (N₂)*μ(N₂)]= =0,72*28/30,88 = 0,652.

4.Средние мольная, объёмная и массовая теплоёмкости смеси при постоянном давлении в пределах температур от t₁ = 126⁰C до t₂ = 528⁰C.

Средняя массовая теплоёмкость смеси при постоянном давлении:

(C_pmсм) =(C_pmсм2*t₂ - C_pmсм1*t₁) / (t₂ – t₁);

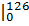(C_pmсм1) = g_CO2* (C_pmCO2) 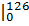+g_N2*(C_pmN2) 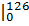+g_CO*(C_pmCO) 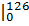= =0,257*0,8773+ 0,652*1,0324 + 0,091*1,0429 =0,994 кДж/(кг*К);

(C_pmсм2) = g_CO2* (C_pmCO2) +g_N2*(C_pmN2) +g_CO* (C_pmCO) = =0,257*1,0203 + 0,652* 1,0598 + 0,091*1,0779 = 1,051кДж/(кг*К);

(C_pmсм) 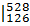= (1,051*528 - 0,994*126)/(528 - 126) = 1,069 кДж/(кг*К).

Средняя мольная теплоёмкость смеси при постоянном давлении:

(μC_pmсм) = (C_pmсм) 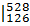*μ_СМ = 1,069*30,88 = 33,011кДж/(кмоль*К).

Средняя объёмная теплоёмкость смеси при постоянном давлении:

(C* _pmсм) = (μC_pmсм) 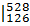/22,4 = 33,011/22,4 = 1,474кДж/(м ³*К).

Ответы на вопросы

1.Что называется газовой постоянной? Как определяется универсальная газовая постоянная? Единицы измерения.

Газовая постоянная R = 8314/μ – отнесена к 1 кг конкретного газа[Дж/(кг*К)], представляет собой удельную работу изменения объема, совершаемую 1 кг рабочего тела при изменении его температуры на 1 К в изобарном процессе.

Универсальная газовая постоянная R = 8314 Дж/(кмоль*К) – отнесена к 1 кмолю - это работа изменения объема, совершаемая 1 кмолем газа при изменении его температуры на 1 К в изобарном процессе.

2.Что представляет собой массовая, объёмная и мольная теплоёмкости? Каковы единицы их измерения в системе СИ? Какова связь между указанными теплоёмкостями?

Удельная молярная теплоемкость(mС) – количество тепла, которое необходимо сообщить 1 кмолю вещества, чтобы повысить его температуру на один градус[кДж/(кмоль*К)].

Удельная массовая теплоемкость (C) – количество тепла, которое необходимо сообщить 1 кг вещества, чтобы повысить его температуру на один градус[кДж/(кг*К)].

Удельная объемная теплоемкость (С¢) -– это количество теплоты, которое необходимо подвести к 1 м³ вещества, чтобы нагреть его на один градус [кДж/(м³*К.)].

Взаимную связь массовой, объемной и мольной теплоемкостей можно выразить следующими соотношениями:

; ;

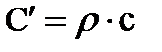
где r - плотность газа;

μ – молярная масса газа.

3.Какие факторы влияют на величину теплоёмкости?

На величину теплоёмкости влияют: температура, давление, количество вещества.

Задача №2.Расчёт политропного процесса сжатия газовой смеси в компрессоре.

Рабочее тело – газовая смесь состава в процентах по объёму: СО₂ = 18%; CO = 10%; N₂ = 72%. Первоначальный объём, занимаемый газовой смесью V₁ = 40 м³. Начальные параметры состояния: давление Р₁ = 0,1 МПа, температура t₁ = 27⁰С. Процесс сжатия происходит при показателе политропы n= 1,22. Давление смеси в конце сжатия Р₂ = 0,9 МПа.

Определить: 1) массу газовой смеси; 2) удельный объём смеси в начале и в конце процесса; 3) объём, занимаемый смесью в конце процесса; 4) температуру в конце процесса; 5) работу сжатия в процессе; 6) работу, затрачиваемую на привод компрессора; 7) изменение внутренней энергии газовой смеси; 8) массовую теплоёмкость рабочего тела в данном процессе; 9) количество тепла, участвующего в процессе; 10) изменение энтропии в процессе.

Построить рассмотренный процесс в координатах p-v и T-s.

Решение:

1.Масса газовой смеси.

Из уравнения состояния

M_см = P₁* V₁ /(R_см*T₁) = 0,1*10⁶*40/(269*300) = 49,57 кг.

2.Объём, занимаемый смесью в конце процесса.

Из соотношения для политропного процесса

V₂ⁿ = Р₁*V₁ⁿ/ Р₂ → V₂^1,22 = 0,1*40^1,22/0,9 =10,006→ V₂ = 6,61 м³.

3.Удельный объём смеси в начале и в конце процесса.

v₁ = V₁/ M_см= 40/49,57 = 0,81 кг/ м³;

v₂ = V₂/ M_см= 6,61/49,57 = 0,13 кг/ м³.

4.Температура газовой смеси в конце процесса.

Из уравнения состояния

Т₂ = V₂*Р₂/(R_см* M_см) = 6,61*0,9*10⁶/(269*49,57) = 446K.

5.Работа сжатия в процессе.

L_сж = [n/(n-1)]*(P₂*V₂ – P₁*V₁) = [1,22/(1,22 -1)]*(0,9*10⁶*6,61 –

- 0,1*10⁶*40) = 10808090 Дж.

6.Работа, затрачиваемая на привод компрессора.

L_k = [M*n*R*T₁/(n-1)]*[(P₂/P₁)^n-1/n -1] = [49,57*1,22*269*300/(1,22-

-1)]*[(0,9/0,1)^1,22-1/1,22 -1] = 10785550 Дж.

7.Массовая изохорная теплоёмкость рабочего тела в данном процессе.

C_vmсм = g_CO*C_vmCO + g_N2*C_vmN2 + g_CO2*C_vCO2 = 0,091*0,7427 + +0,652*0,7352 +0,257*0,6259 = 0,708 кДж/(кг*К).

8. Массовая изобарная теплоёмкость рабочего тела в данном процессе:

C_рmсм = g_CO*C_рmCO + g_N2*C_рmN2 + g_CO2*C_рCO2 = 0,091*1,0396 + +0,652*1,0304 +0,257*0,8148 = 0,976 кДж/(кг*К).

9. Показатель адиабаты смеси:

k = C_рmсм / C_vmсм = 0,976/0,708 = 1,38.

10.Изменение внутренней энергии газовой смеси.

∆U = [(n – 1)/(1 – k)]*L = [(1,22 – 1)/(1 – 1,38)]* 10785550 = - 6244266 Дж.

11.Количество теплоты, участвующее в процессе.

Q = [(k – n)/(k – 1)]*L =[(1,38 – 1,22)/(1,38 – 1)]* 10785550 = 4541284 Дж.

12. Изменение энтропии в процессе.

∆S = M*C_vmсм* [(n – k)/(n – 1)]* ln(T₂/T₁),

∆S = 49,57*708* [(1,22 – 1,38)/(1,22 – 1)]*ln(446/300) = - 10121 Дж/К.

Изображение процесса в координатах p-v и T-s координатах.

V,м3

11 1

Р, МПа

 

S,кДж/(кг*К)

T,К

Ответы на вопросы

1.В каких пределах может изменяться показатель политропного процесса?

В общем случае показатель политропы сжатия может быть любым, однако на практике реализуется показатель политропы от k до 1 (1<n<k).

n=1 – изотермически компрессор;

n=k – адиабатный компрессор.

2.В каких пределах может изменяться теплоёмкость рабочего тела в политропном процессе?

Численно теплоемкость изменяется в пределах от -∞ до +∞, зависит от показателя политропы и адиабаты: С = C_v*[(n-k)/(n-1)].

3.Как выглядит уравнение 1-го закона термодинамики применительно к рассмотренному в задаче процессу?

Так как в политропном процессе происходит изменение внутренней энергии и совершается работа, то 1 закон термодинамики имеет вид:

Q = L + ∆U.

4.Как зависит работа, затрачиваемая на привод компрессора, от показателя политропы, почему?

С увеличением показателя политропы работа, затрачиваемая на привод компрессора, согласно уравнению L_k = [n*R*T₁/(n-1)]*[(P₂/P₁)^n-1/n -1], уменьшается.

Поделиться:

Воспользуйтесь поиском по сайту: