Основные теоретические положения

Лабораторная работа №3

Выполнил Садиков А. А. гр 2315

ЭЛЕКТРОТЕПЛОВАЯ АНАЛОГИЯ

Цель работы:

Получить представление о сущности метода аналогии и его математическом описании; ознакомиться с экспериментальными методами исследования с использованием методов аналогий.

ВВЕДЕНИЕ

Экспериментальные исследования подразделяются на натурные и модельные. Натурные исследования проводятся на действующем объекте и позволяют получать наиболее полные и надежные характеристики объекта. Модельные исследования проводятся на специально создаваемых стендах – экспериментальных установках, и позволяют детально изучить отдельные процессы, протекающие в реальных объектах.

Исследования на моделях проводят с учетом правил моделирования (подобия). Процессы различной физической природы, которые описываются математически тождественными уравнениями и условиями однозначности, называются аналогичными. Такая аналогия существует, например, между явлениями теплопроводности и диффузии. К исследованиям по методу аналогий прибегают тогда, когда удается подобрать процесс, который существенно легче осуществить экспериментально, чем натурный, и в котором измерения проводятся с большей точностью.

 

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Процесс теплопроводности в области GT (x,y,z) имитируется прохождением электрического тока в геометрической подобной электропроводящей области Gэ (x,y,z). На границах области Gэ (x,y,z) организуется подвод электрического тока I или задаются электрические потенциалы u с соблюдением подобия в краевых условиях модели и натурного образца.

Явления теплопроводности и электропроводности описываются уравнениями:

(1)

где dQ и dI – элементарные потоки теплоты и электрического тока, прошедшие через площадки dFT и dFэ в направлении нормалей nT и nэ; Т и u – температура и электрический потенциал; l и s - коэффициенты теплопроводности и электропроводности, индексы «Т» и «Э» отмечают величины, относящиеся к тепловым и электрическим явлениям.

Применение указанных уравнений к случаю двумерной задачи при стационарных условиях протекания процессов и независимости физических свойств l, s от температуры приводит к уравнениям Лапласа:

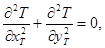
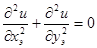(2)

Пусть граничные условия (третьего ряда) задаются в виде:

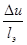- grad T = - grad u = (3)

Введем безразмерные величины:

XТ = xТ /lот, YT = yT/lот, LT = lT/ lот, q = DT/DT0,

Где величины с индексом о являются характерными для данного процесса. Такие же соотношения вводятся и для величин, относящихся к электрическому явлению.

После постановки этих соотношений уравнения (2) и граничные условия (3) принимают безразмерный вид:

, , (4)

- grad q = q/LT, - grad u = u/Lэ. (5)

Тождественность приведенных уравнений имеет место при любом выборе масштабов для температуры и электрического потенциала. Решения дифференциальных уравнений теплопроводности и электропроводности (4) тождественно одинаковы при условии LT = Lэ.

Из этого условия выходит, что qi = ui, следовательно:

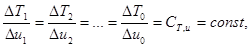(6)

т.е. распределение температуры и электрического потенциала подобны и имеет место аналогия.

При исследовании нестационарных процессов для одномерных областей исходные уравнения имеют вид:

, (7)

где Rэ и Сэ электрические сопротивление и емкость на единицу длины. Из сравнения этих уравнений следует, что аналогия устанавливается, если выполняется условие:

Изменение теплового потока пропорционально теплоемкости системы и изменению температуры:

 

Следовательно, в модели теплоемкости могут быть воспроизведены соответствующими электрическими емкостями.

При описании электрических моделей, имитирующих процессы теплопроводности, применяются два способа. По первому способу электрические модели повторяют геометрию тепловой системы и изготовляются из материала с непрерывной электропроводностью.

Наряду с такими моделями применяются электрические модели с электрическими цепями (сопротивлениями, емкостями), которые используются при описании наиболее сложных явлений, как правило, нестационарных.

Если область GT(х,у) выполнена из материалов с различными значениями l, то область GT(х,у) изготавливают составной. Части областей с различными l моделируют либо несколькими слоями из одного и того же материала, либо слоями из различных материалов с соблюдением пропорциональности между l и s.

Термические сопротивления теплоотдачи (внешние) на поверхностях исследуемой системы учитываются путем добавления к электрической модели дополнительных слоев или сопротивлений RЭ.

НАХОЖДЕНИЕ ДВУМЕРНОГО СТАЦИОНАРНОГО ПОЛЯ ТЕМПЕРАТУР В ПОПЕРЕЧНОМ СЕЧЕНИИ ОБРАЗЦА.
Пусть на наружном контуре образца 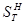(рис.1) задано распределение температуры Т (S 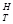), на внутреннем контуре 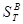происходит конвективный теплообмен с теплоносителем со средней температурой Т+. Задано распределение местных коэффициентов теплоотдачи . Необходимо определить температурное поле внутри образца Т (х,у).

 

 

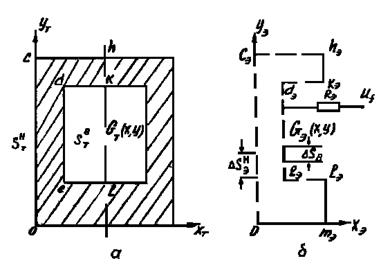
Рис. 1. Электромоделирование поля температуры

а) двумерная тепловая область с симметрией;

б) электропроводная область из листового материала

Из листового проводящего материала вырезается область Gэ(х,у) геометрически подобная область GT(х,у). Масштаб выбирается из соображения удобства. Наружный и внутренний контуры модели разбиваются на участки S и S , на которые накладываются электрические шины. При сложном изменении граничных условий производится разбиение на мелкие участки, а на участках с постоянными граничными условиями накладываются шины большего размера. На участках наружного контура D S задаются потенциалы, соответствующие температурам Т(S ).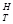

Пересчет температур на потенциалы производится по формуле:

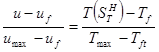(8), где Тmax и umax – максимальная из температур Т(S 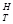) и соответствующая ей потенциал в сходственном участке, uf – потенциал, соответствующий температуре Тf.

К участкам внутреннего контура присоединяются сопротивления Rэ, значения которых определяются из соотношения:

(9), где и характерные (обычно максимальные) размеры областей GT(x,y) и Gэ(x,y).

Формула (9) находится из равенства чисел Био для тепло- и электропроводных областей.

Безразмерные потенциалы U = (u-ut)/(umax-ut) равны безразмерным температурам Q = (T-Tf)/(Tmax-Tf), в сходственных точках Х = хТ/LT = xэ/LТ и Y = YT/ LT = Yэ/ Lэ.

Из этих соотношений можно найти искомую температуру:

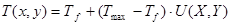(10)

При симметрии температурного поля моделируют часть области GT(x,y), отделяемой от остальной по линиям симметрии (рис.1). Поверхности по линиям симметрии являются адиабатными.

Поделиться:

Воспользуйтесь поиском по сайту: