Затухающие электрические колебания. Автоколебания. Генератор незатухающих колебаний(на транзисторе)

Свободные электромагнитные колебания в контуре. Превращение энергии в колебательном контуре

Механические колебания представляют собой вид движения тел. На все вопросы, касающиеся таких колебаний, можно получить ответ в кинематике и динамике. Наряду с механическими колебаниями и колебательными системами существуют электрические колебания и колебательные системы. Для техники такие системы имеют еще большее значение, чем механические.

Возникает вполне закономерный вопрос: что именно и каким образом колеблется в этом случае?

Может колебаться электрический заряд на обкладках конденсатора, электрический ток в проводниках, электродвижущая сила на клеммах генератора, напряжение на каком-либо сопротивлении и т. д. Таким образом, в данном случае колеблются электрические величины. В данном случае, говоря о колебаниях электрических величин, подразумевается, что они не остаются постоянными, а меняются с течением времени. Также, подобно тому, как не всякое механическое движение является колебанием, так и не всякое изменение электрических величин со временем есть электрическое колебание.

Для механических колебаний существенной чертой является повторяемость движения, то есть его периодичность. Эта же черта является существенной и для электрических колебаний. Если изменение какой-либо электрической величины, например тока, происходит периодически, повторяясь, то можно назвать такое изменение электрическим колебанием. Примером такого процесса является всем нам известный переменный ток в осветительной электросети, который меняется по закону гармонического колебания.

Электрические колебания человек не может воспринимать непосредственно, подобно тому как он воспринимает колебания механические, например, видит колебания маятника или слышит колебания камертона. Однако, мы знаем, что и электрически заряженные тела, и проводники, по которым течет электрический ток, взаимодействуют между собой с некоторыми силами. На измерении этих сил основано измерение самих электрических величин: зарядов, токов, напряжений и т. д. Благодаря этим силам получается механическое движение в электродвигателях. С помощью этих же (электростатических и электродинамических) сил можно самыми различными способами превратить электрические колебания в механические. Например, одним из способов превращения колебаний тока в механические колебания состоит в использовании поворота катушки с током в магнитном поле. На этом основано устройство осциллографа.

Колебательный контур.

Переменный ток в осветительной сети получается потому, что генераторы на электростанции дают переменную электродвижущую силу. Такая электродвижущая сила возникает, например, в проволочной рамке, равномерно вращающейся в магнитном поле, причем ее период определяется угловой скорость вращения рамки. Таким образом, колебания тока в цепи вызываются колебаниями электродвижущей силы, действующей в этой цепи, подобно тому как вынужденные колебания тела вызываются колебаниями приложенной к нему механической силы. Колебания тока являются в данном случае вынужденными колебаниями.

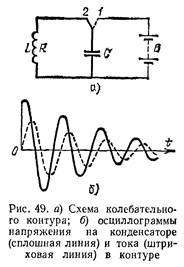
Но существуют такие электрические цепи, в которых могут происходить свободные электрические колебания, то есть колебания без действия какой-либо внешней периодической электродвижущей силы, другими словами, существуют электрические колебательные системы. Простейшей системой такого рода является колебательный контур. Так называется цепь, которая получается при подсоединении конденсатора к катушке индуктивности (рис 49а.). Электрические свойства такой цепи определяются емкостью С конденсатора, индуктивностью L катушки и сопротивлением цепи (то есть в основном катушки) R. Для того чтобы возникли свободные колебания, надо каким-либо способом нарушить состояние равновесия – зарядить конденсатор или возбудить (индуцировать) ток, а затем предоставить контур самому себе. На рис 49,а. контур выводится из состояния равновесия тем, что конденсатору сообщается начальный заряд. Для этого служат батарея и переключатель. При одном положении переключателя (положение 1 на рис.49а) контур разомкнут и конденсатор подключен к батарее, которая и заряжает его до напряжения на клеммах батареи. Переводя переключатель в положение 2, мы отключаем батарею и замыкаем контур. С этого момента в контуре и начинаются свободные электрические колебания: заряд и напряжение на конденсаторе попеременно меняет знак, проходя через нулевое значение (на рис. 49,б показано сплошной линией). Аналогичным образом меняется ток в контуре (штриховая линия на том же рисунке), но со сдвигом по времени: ток проходит через нуль приблизительно в те моменты, когда напряжение на конденсаторе имеет наибольшие положительные и отрицательные значения.

Чем меньше сопротивление контура R, тем меньше затухание колебаний и тем точнее совпадают по времени моменты прохождения тока через нуль с моментами наибольших значений напряжения на конденсаторе. В идеальном случае полного отсутствия сопротивления колебания тока и напряжения изображались бы двумя синусоидами, сдвинутыми на четверть периода. Рассмотрим электрические колебания в идеальном, т. е. не имеющем сопротивления, колебательном контуре. В данном случае свободные незатухающие колебания называются собственными. Магнитное поле не может мгновенно появиться или исчезнуть. Всякое изменение магнитного поля сопровождается возникновением электродвижущей силы индукции, которая вызывает в проводах индукционный ток. Направление этого тока по закону Ленца таково, что создаваемое им магнитное поле стремится компенсировать изменение магнитного поля, вызывающего индукцию. Это индукционное магнитное поле замедляет изменение начального поля, препятствуя его мгновенному исчезновению или появлению. Таки образом, получается, что магнитное поле обладает инерцией подобно инерции тела. Тело не может мгновенно остановиться или сдвинуться с места, так как это означало бы, что оно приобретает бесконечно большое ускорение и, следовательно, по закону Ньютона, потребовало бы бесконечно большой силы.

Когда мы замыкаем заряженный конденсатор на катушку, то в первый момент напряжение на конденсаторе максимально, а ток в цепи равен нулю. Однако с этого момента начинается движение зарядов, перетекающих с одной обкладки на другую и, поэтому появляется ток, вызывающий магнитное поле. Магнитное поле, а значит, и обусловливающий его ток не могут мгновенно принять свое максимальное значение, а будут нарастать постепенно. Поскольку ток переносит заряды с одной обкладки на другую, напряжение на конденсаторе постепенно падает (конденсатор разряжается). Таким образом, увеличение индукции магнитного поля идет параллельно с убыванием напряженности электрического поля. Это соответствует закону сохранения энергии, так как согласно ему увеличение энергии магнитного поля должно сопровождаться уменьшением энергии электрического поля. Поэтому, когда напряжение на конденсаторе станет равным нулю и электрическая энергия исчезнет, магнитная энергия достигнет максимума. В этот момент будут максимальными и ток и индукция магнитного поля в катушке.

Так как магнитное поле (а значит, и ток) не может сразу исчезнуть, то перетекание заряда будет продолжаться в том же направлении и конденсатор начнет заряжаться, но обкладка, бывшая ранее отрицательной, будет теперь заряжаться положительно, и обратно. Ток будет ослабевать и в определенный момент обратится в нуль, конденсатор же в этот момент будет вновь заряжен до наибольшего напряжения, но с обратным знаком. Далее, ток будет течь в обратную сторону, так что в итоге конденсатор вновь перезарядится, т. е. мы вернемся к исходному состоянию, которое было в момент замыкания переключателя. На рис. 50 показаны пять состояний контура – через каждые четверть периода, последний рисунок (по истечении полного периода) совпадает с первым. Штриховыми линиями показаны линии электрического поля в конденсаторе и линии магнитного поля в катушке.

 

Если сопротивление контура R=0 то колебательный контур называют идеальным.

Свободные электромагнитные колебания в контуре – это периодические изменения зарядаq и напряжения u на обкладках конденсатора и силы тока i, текущего через катушку индуктивности и резистор.

Колебания в контуре можно вызвать, сообщив обкладкам конденсатора некоторый начальный заряд или возбудив в катушке индуктивности электрический ток (например, путем включения внешнего магнитного поля, пронизывающего витки катушки). Процесс колебаний в такой цепи заключается в периодической перезарядке конденсатора под действием ЭДС самоиндукции и в протекании переменного тока.

В идеальном колебательном контуре устанавливаются незатухающие гармонические колебания, при которых величина заряда q, напряжения u и силы тока i, изменяются по следующим законам:

q = q₀∙cos(ω₀t),

u = ,

i = q` = q_m∙ω₀∙cos(ω₀t - ) = I_m∙cos(ω₀t - )

q, u, i – мгновенные значения заряда, напряжения и силы тока.

q_m,u_m= q_m/C_, I_m= q_m∙ ω – амплитудные значения заряда, напряжения и силы тока.

ω₀ – циклическая частота свободных колебаний в контуре.

Колебания заряда и напряжения совершаются в одной и той же фазе, а колебания силы тока отстают по фазе от напряжения на конденсаторе на .

Период свободных электромагнитных колебаний определяется формулой Томсона: T₀ = 2 π

Частота свободных электромагнитных колебаний: ν₀= =

Циклическая частота свободных электромагнитных колебаний::ω₀ = 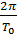= 2πν₀ =

При колебаниях в контуре происходит непрерывный переход энергии электрического поля конденсатора в энергию магнитного поля катушки индуктивности, и наоборот. При незатухающих колебаниях энергия, запасенная в колебательном контуре в начальный момент времени, не изменяется с течением времени и равна: W =

Затухающие электрические колебания. Автоколебания. Генератор незатухающих колебаний(на транзисторе)

Свободные колебания всегда затухают из-за потерь энергии (трение, сопротивление среды, сопротивление про­водников электрического тока и т. п.). Между тем и в тех­нике и в физических опытах крайне нужны незату­хающие колебания,периодичность которых сохра­няется все время, пока система вообще колеблется. Как по­лучают такие колебания? Мы знаем, что вынужденные коле­бания, при которых потери энергии восполняются работой периодической внешней силы, являются незатухающими. Но откуда взять внешнюю периодическую силу? Ведь она в свою очередь требует источника каких-то незатухающих колебаний.

Незатухающие колебания создаются такими устройства­ми, которые сами могут поддерживать свои колебания за счет некоторого постоянного источника энергии. Такие устройства называются автоколебательными системами. На рис. 55 изображен пример электромеханического устройства такого рода. Груз висит на пружине, нижний конец которой погружается при колебаниях этого пружинного маятника в чашечку со ртутью. Один полюс батереи присоединен к пружине наверху, а другой — к чашечке со ртутью. При опускании груза электрическая цепь замы­кается и по пружине проходит ток. Витки пружины благодаря магнит­ному полю тока начинают при этом притягиваться друг к другу, пру­жина сжимается, и груз получает толчок кверху. Тогда контакт раз­рывается, витки перестают стяги­ваться, груз опять опускается вниз, и весь процесс повторяется снова.

Таким образом, колебание пру­жинного маятника, которое само по себе затухало бы, поддерживается периодическими толчками, обуслов­ленными самим колебанием маятника. При каждом толчке батарея отдает порцию энер­гии, часть которой идет на подъем груза. Система сама управляет действующей на нее силой и регулирует поступ­ление энергии из источника — батареи. Колебания не зату­хают именно потому, что за каждый период от батареи отби­рается как раз столько энергии, сколько расходуется за то же время на трение и другие потери. Что же касается перио­да этих незатухающих колебаний, то он практически совпа­дает с периодом собственных колебаний груза на пружине, т. е. определяется жесткостью пружины и массой груза.

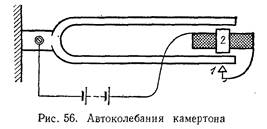
Подобным же образом возникают незатухающие колеба­ния молоточка в электрическом звонке, с той лишь разни­цей, что в нем периодические толчки создаются отдельным электромагнитом, притягивающим якорек, укрепленный на молоточке. Аналогичным путем можно получить автоколе­бания со звуковыми частотами, например, возбудить неза­тухающие колебания камертона (рис. 56). Когда ножки камертона расходятся, замыкается контакт 1; через обмотку электромагнита 2 проходит ток, и электромагнит стягивает ножки камертона. Контакт при этом размыкается, и далее следует повторение всего цикла. Чрезвычайно существенна для возникновения колеба­ний разностьфазмеждуколебанием и силой, которую оно регулирует. Перенесем контакт 1 с внешней стороны ножки камертона на внутреннюю. Замы­кание происходит теперь не при расхождении, а при сбли­жении ножек, т. е. момент включения электромагнита передвинут на полпериода по сравнению с предыдущим опытом. Легко видеть, что в этом случае камертон будет все время сжат непрерывно включен­ным электромагнитом, т. е. колеба­ния вообще не возникнут.

Электромеханические автоколеба­тельные системы применяются в тех­нике очень широко, но не менее рас­пространенными и важными являют­ся и чисто механические автоколеба­тельные устройства. Достаточно ука­зать на любой часовой механизм. Незатухающие колебания маятника или балансира часов поддерживают­ся за счет потенциальной энергии поднятой гири или за счет упругой энергии заведенной пружины.

Автоколебаниями являются также колебания струны под действием смычка (в отличие от свободных колебаний стру­ны у рояля, арфы, гитары и других несмычковых струнных инструментов, возбуждаемых однократным толчком или рывком); автоколебаниями являются звучание духовых музыкальных инструментов, движение поршня паровой машины и многие другие периодические процессы.

Характерная черта автоколебаний состоит в том, что их амплитуда определяется свойствами самой системы, а не начальным отклонением или толчком, как у свободных ко­лебаний. Если, например, маятник часов отклонить слиш­ком сильно, то потери на трение будут больше, чем поступ­ление энергии от заводного механизма, и амплитуда будет уменьшаться. Наоборот, если уменьшить амплитуду, то избыток энергии, сообщаемой маятнику ходовым колесом, заставит амплитуду возрасти. Автоматически установится именно такая амплитуда, при которой расход и поступление энергии сбалансированы.

Устройства, объединяемые под названием автоколебательные системы, характеризуются следующими от­личительными свойствами.

Автоколебательные системы способны генерировать незату­хающие колебания. Эти колебания могут быть гармонически­ми (синусоидальными) или более сложной формы, но они могут продолжаться неограниченно долго, до тех пор, пока не вышли из строя элементы, образующие систему.

Автоколебательные системы отличаются от колебательного контура с сопротивлением, равным ну­лю. Такой контур представляет собой предельный случай, недо­стижимый на практике. Автоколебательные же системы суть реальные устройства, сопротивление которых не равно нулю.

В автоколебательных системах незатухающие колебания воз­никают под влиянием процессов, происходящих внутри системы, и для их поддержания не требуется никаких внешних воздей­ствий. В этом отношении автоколебания радикально отличаются от вынужденных колебаний, которые также могут быть незату­хающими, но для своего существования требуют периодических внешних воздействий (в механике — внешних сил, в электриче­стве — приложенных извне напряжений).

В состав автоколебательных систем входит источник энергии (в случае механических колебаний — сжатая пружина, поднятый груз и т.д., в случае электрических — батарея или иной источник тока). Этот источник периодически включается самой системой и вводит в нее определенную энергию, компенсирующую поте­ри на выделение тепла Джоуля-Ленца, что и делает колебания незатухающими.

Так как колебания в автоколебательных системах устанав­ливаются под влиянием процессов, происходящих внутри систе­мы, то они возникают самопроизвольно (самовозбуждение), под действием случайных малых воздействий, выводящих систему из равновесия (флуктуации). Возникшие малые колебания са­мопроизвольно нарастают, и в конце концов в системе образу­ются установившиеся колебания, свойства которых (частота, ин­тенсивность, форма) определяются параметрами системы и не зависят от начальных условий.

Как создать незатухающие колебания в контуре? Известно, что если конденсатор колебательного контура зарядить, то в контуре возникнут затухающие колебания. В конце каждого периода колебаний заряд на пластинах конденсатора имеет меньшее значение, чем в начале периода. Суммарный заряд, конечно, сохраняется (он всегда равен нулю), но происходит уменьшение положительного заряда одной пластины и отрицательного заряда другой на равные по модулю значения. В результате энергия колебаний уменьшается, так как она пропорциональна квадрату заряда одной из пластин конденсатора. Чтобы колебания не затухали, нужно компенсировать потери энергии за каждый период.

Пополнять энергию в контуре можно, подзаряжая конденсатор. Для этого надо периодически подключать контур к источнику постоянного напряжения. Конденсатор должен подключаться к источнику только в те интервалы времени, когда присоединенная к положительному полюсу источника пластина заряжена положительно, а присоединенная к отрицательному полюсу — отрицательно (рис. 4.21). Только в этом случае источник будет подзаряжать конденсатор, пополняя его энергию.

Если же ключ замкнуть в момент, когда присоединенная к положительному полюсу источника пластина имеет отрицательный заряд, а присоединенная к отрицательному полюсу — положительный, то конденсатор будет разряжаться через источник (рис. 4.22). Энергия конденсатора при этом будет убывать.

Следовательно, источник постоянного напряжения, постоянно подключенный к конденсатору контура, не может поддерживать в нем незатухающие колебания, так же как постоянная сила не может поддерживать механические колебания. В течение половины периода энергия поступает в контур, а в течение следующей половины периода возвращается в источник. В контуре незатухающие колебания установятся лишь при условии, что источник будет подключаться к контуру в те интервалы времени, когда возможна передача энергии конденсатору. Для этого необходимо обеспечить автоматическую работу ключа (или клапана, как его часто называют). При высокой частоте колебаний ключ должен обладать надежным быстродействием. В качестве такого практически безынерционного ключа и используется транзистор.

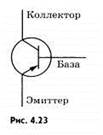
Транзистор состоит из трех различных полупроводников: эмиттера, базы и коллектора. Эмиттер и коллектор имеют одинаковые основные носители заряда, например дырки (это полупроводник р-типа), а база имеет основные носители противоположного знака, например электроны (полупроводник n-типа). Схематическое изображение транзистора показано на рисунке 4.23.

Работа генератора на транзисторе. Упрощенная схема генератора на транзисторе показана на рисунке 4.24. Колебательный контур соединен последовательно с источником напряжения и транзистором таким образом, что на эмиттер подается положительный потенциал, а на коллектор —отрицательный. При этом переход эмиттер — база (эмиттерный переход) является прямым, а переход база — коллектор (коллекторный переход) оказывается обратным, и ток в цепи не идет. Это соответствует разомкнутому ключу на рисунках 4.21, 4.22.

Чтобы в цепи контура возникал ток и подзаряжал конденсатор контура в ходе колебаний, нужно сообщать базе отрицательный относительно эмиттера потенциал, причем в те интервалы времени, когда верхняя (см. рис. 4.24) пластина конденсатора заряжена положительно, а нижняя — отрицательно. Это соответствует замкнутому ключу на рисунке 4.21.

В интервалы времени, когда верхняя пластина конденсатора заряжена отрицательно, а нижняя — положительно, ток в цепи контура должен отсутствовать. Для этого база должна иметь положительный потенциал относительно эмиттера.

Таким образом, для компенсации потерь энергии колебаний в контуре напряжение на эмиттерном переходе должно периодически менять знак в строгом соответствии с колебаниями напряжения на контуре. Необходима, как говорят, обратная связь.

Обратная связь в рассматриваемом генераторе — индуктивная. К эмиттерному переходу подключена катушка индуктивностью Lсв, индуктивно связанная с катушкой индуктивностью L контура. Колебания в контуре вследствие электромагнитной индукции возбуждают колебания напряжения на концах катушки, а тем самым и на эмиттерном переходе. Если фаза колебаний напряжения на эмиттерном переходе подобрана правильно, то «толчки» тока в цепи контура действуют на контур в нужные интервалы времени, и колебания не затухают. Напротив, амплитуда колебаний в контуре возрастает до тех пор, пока потери энергии в контуре не станут точно компенсироваться поступлением энергии от источника. Эта амплитуда тем больше, чем больше напряжение источника. Увеличение напряжения приводит к усилению «толчков» тока, подзаряжающего конденсатор.

Генераторы на транзисторах широко применяются не только во многих радиотехнических устройствах: радиоприемниках, передающих радиостанциях, усилителях и т. д., но и в современных электронно-вычислительных машинах.

Основные элементы автоколебательной системы. На примере генератора на транзисторе можно выделить основные элементы, характерные для многих автоколебательных систем (рис. 4.25).

1. Источник энергии, за счет которого поддерживаются незатухающие колебания (в генераторе на транзисторе это источник постоянного напряжения).

 

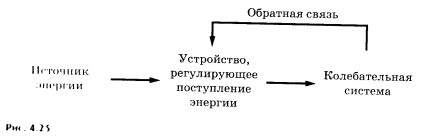
2. Колебательная система — та часть автоколебательной системы, непосредственно в которой происходят колебания (в генераторе на транзисторе это колебательный контур).
3. Устройство, регулирующее поступление энергии от источника в колебательную систему, — клапан (в рассмотренном генераторе роль клапана выполняет транзистор).
4. Устройство, обеспечивающее обратную связь, с помощью которой колебательная система управляет клапаном (в генераторе на транзисторе предусмотрена индуктивная связь катушки контура с катушкой в цепи эмиттер — база).

 

Вопросы: (СОСТАВИТЬ В ТЕТРАДИ КОНСПЕКТ ПУТЕМ ОТВЕТА НА НИХ!)

1. Что может колебаться в электрической цепи?

2. Что такое колебательный контур?

3. Нарисуйте схему колебательного контура.

4. Чем определяются свойства такой цепи как колебательный контур?

5. Какой колебательный контур называется идеальным?

6. Что представляет собой колебательный процесс в колебательном контуре?

7. Укажите формулы (законы), по которым изменяются заряд, ток и напряжение.

8. По какой формуле определяется период свободных электромагнитных колебаний?

9. По какой формуле определяется частота свободных электромагнитных колебаний?

10. По какой формуле определяется циклическая частота свободных электромагнитных колебаний?

11. Что такое автоколебательная система?

12. В чем отличие автоколебаний от вынужденных и свободных колебаний?

13. Как устроен транзистор?

14. Какова роль транзистора в генерации автоколебаний?

15. Как осуществляется обратная связь в генераторе на транзисторе?

16. Укажите основные элементы автоколебательной системы.

17. Какие колебания называются незатухающими?

18. Какие колебания называются вынужденными?

19. Опишите, каким образом осуществляются автоколебания пружинного маятника.

20. Где применяются автоколебательные системы?

21. Укажите характерную черту автоколебаний.

22. Укажите свойства автоколебательных систем (по пунктам 1,2,3 и так далее, все сколько их есть)

23. Какую роль играет источник энергии в составе автоколебательной системы?

24. Укажите причины, приводящие к затуханию колебаний (написать самостоятельно, в этом тексте нет).

25. Зарисуйте схему и опишите процесс создания незатухающих колебаний в контуре.

26. Для чего используется транзистор в генераторе?

27. Зачем нужна обратная связь?

28. Зарисуйте схему и опишите поэтапно процесс работы генератора на транзисторе.

Поделиться:

Воспользуйтесь поиском по сайту: