Расчет изгибаемых элементов

Лекция 16

РАСЧЕТ ЭЛЕМЕНТОВ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ

ПО ОБРАЗОВАНИЮ И РАСКРЫТИЮ ТРЕЩИН

(II ГРУППА ПРЕДЕЛЬНЫХ СОСТОЯНИЙ)

Общие сведения

Ко II группе предельных состояний относят расчет элементов по пригодности к нормальной эксплуатации, т.е. расчет по трещиностойкости и деформациям (прогибам)

Трещиностойкость железобетонных элементов – это сопротивление образованию трещин в стадии I НДС или сопротивление чрезмерному их раскрытию трещин в стадии II НДС.

В железобетонных элементах трещины могут быть вызваны условиями твердения бетона (усадки) или перенапряжением материалов (перегрузкой, осадкой опор, изменением температуры). Трещины от перенапряжения появляются чаще в растянутых зонах.

Трещины в растянутой зоне изгибаемых конструкций, не заметные на глаз, появляются при эксплуатационных нагрузках даже в безукоризненно выполненных железобетонных конструкциях. Возникновение их вызвано малой растяжимостью бетона, не способного следовать за значительными удлинениями арматуры при высоких рабочих напряжениях.

Трещина в сжатых частях указывают на несоответствие размеров сечения усилиям сжатия, являются опасными для прочности конструкции.

Трещины понижают жесткость конструкции и нарушают ее монолитность, что имеет особенное значение для конструкций, подверженных действию вибрационных и динамических нагрузок.

Наличие трещин в железобетонных конструкциях облегчает доступ влаги и агрессивных газов к арматуре, что может вызвать ее коррозию; кроме того, бетон с трещинами значительно легче выветривается.

Различают три этапа в образовании трещин:

1. возникновение трещин (невидимые трещины);

2. появление (образование) трещин () – трещины становятся видимыми невооруженным глазом;

3. раскрытие трещин до предельно допустимых величин

Основные гипотезы:

1. Перед образованием трещин напряжения в растянутом бетоне принимаются равными расчетному сопротивлению растяжению по 2 группе предельных состояний, т.е. ;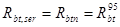

2. При расчете по образованию трещин действует принцип суперпозиции – принцип независимости действия сил.

– если есть напрягаемая арматура;

– при ненапрягаемой арматуре.

3. Действует гипотеза плоских сечений.

Железобетонные конструкции могут эксплуатироваться с видимыми невооруженным глазом трещинами в растянутой зоне с ограничением по ширине раскрытия. Расчет по образованию трещин ведется по стадии I НДС; расчет по раскрытию трещин – по стадии II НДС. До образования трещин выполняется условие совместной деформации арматуры и растянутого бетона.

 

 

Стадия I НДС

 

коэффициент полноты эпюры напряжений в сжатой зоне;

коэффициент полноты эпюры напряжений в растянутой зоне.

, отсюда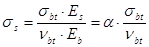

 

 

Рис. 16.1. Стадия I НДС

Стадия Iа НДС

Рис. 16.2. Стадия Iа НДС

–из опытов, тогда .

Стадия II НДС

Зависимость между средней высотой сжатой зоны х и высотой сжатой зоны с трещиной х_ф определяется как .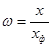

Рис. 16.3. Стадия II НДС

Расчет центрально растянутых элементов

 

При центральном растяжении железобетонной призмы зависимость будет различной на стадиях I и II НДС.

При расчете по 1 и 2 категориям трещиностойкости расчетная нагрузка принимается с учетом коэффициента по нагрузке , при расчете по 3 категории трещиностойкости – .

В стадии I НДС (до появления трещин в бетоне) сопротивление растягивающей силе оказывает бетон с напряжением и продольная арматура с напряжением .

Рис. 16.4. Стадия I НДС при центральном растяжении

 

,

где N – внешняя нагрузка, определяемая с коэффициентом надежности по нагрузке

усилие образования трещин.

В стадии Iа НДС

или

Если используется преднапряжение, то в формулу добавляется еще одно слагаемое, т.е.

,

где Р – усилие обжатия с учетом всех потерь на момент расчета.

В стадии II НДС (после появления трещин) сопротивление растяжению оказывают: в сечении с трещиной – только арматура; на участке между трещинами – бетон и арматура.

На участках между трещинами длиной по данным опытов сцепление между арматурой и бетоном не нарушается. По мере удаления от краев трещины растягивающие напряжения в бетоне увеличиваются. В арматуре происходит обратное явление: в сечении с трещиной напряжение имеет максимальное значение, а по мере удаления от краев трещины оно убывает.

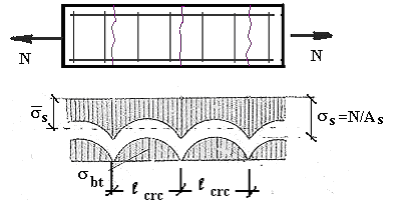
Рис. 16.5. Стадия II НДС при центральном растяжении

 

Напряжения и деформации арматуры в сечении с трещиной равны:

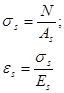
Условные средние напряжения и средние деформации арматуры на участках между трещинами будут

Коэффициент учитывает работу растянутого бетона на участках между трещинами.

 

Расчет изгибаемых элементов

 

Стадия I НДС

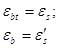
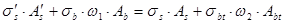
Рис. 16.6. Стадия I НДС изгибаемого элемента

 

 

Стадия Iа НДС

В растянутой арматуре напряжения равны , в бетоне сжатой зоны при

 

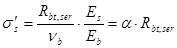
Рис. 16.7. Стадия Iа НДС изгибаемого элемента

 

В стадии Iа каждая единица площади сечения арматуры по сравнению с бетоном воспринимает в сжатой зоне в α раз большее напряжение, а в растянутой – в 2×α раз большее.

Стадия II НДС

 

При изгибе в стадии II НДС растянутая зона элемента разделяется трещинами на участки длиной , и в сечениях с трещинами, как только они появились, растягивающие усилия воспринимаются только продольной арматурой. Опыты показывают, что на величину расстояния влияют поперечные силы, однако в зоне максимальных моментов и при чистом изгибе трещины по длине балки располагаются на приблизительно равных расстояниях.

Рис. 16.8. Стадия II НДС изгибаемого элемента

 

По высоте сечения деформации при изгибе в стадии II изменяются нелинейно, т.к. вследствие нарушения равновесия в момент внутренних сил в момент разрыва бетона растянутой зоны появляются силы сдвига, искривляющие сечение. По длине элемента деформации сжатой и растянутой зон сечения и высота сжатой зоны также переменные, а нейтральная ось волнообразная.

Дополнительные гипотезы:

1. После образования трещин для условного среднего сечения сохраняется гипотеза плоских сечений;

2. Трещины при росте их вверх поднимают нейтральный слой в сторону сжатой зоны. Форма нейтрального слоя нелинейная.

3. Между трещинами растянутый бетон в работе участвует.

4. Для условного среднего сечения на участке с трещинами выполняется гипотеза плоских сечений (рис. 16.8).

Исходя из подобия треугольников (рис. 16.8), получаем:

где коэффициент, учитывающий неравномерность напряжений и деформаций в сжатой зоне;

деформации в сечении с трещиной;

деформации в блоке с трещиной

 

4. Момент образования трещин в изгибаемых элементах по способу ядровых моментов

Нормы (СНиП 2.03.01-84*) рекомендуют определять момент образования трещин приближенно по способу ядровых моментов. Задачу о НДС сечения в стадии I перед образованием трещин от совместного действия внешней нагрузки и усилия обжатия приближенно можно решить как линейную задачу внецентренного сжатия, применив принцип независимости действия сил.

Расчет изгибаемых, внецентренно сжатых, а также внецентренно растянутых элементов по образованию трещин производится из условия:

,

где момент внешних сил, расположенных по одну сторону от рассматриваемого сечения, относительно оси, параллель­ной нулевой линии и проходящей через ядровую точку, наиболее удаленную от растянутой зоны, трещинообразование которой проверяется

;

момент, воспринимаемый сечением, нормальным к продольной оси элемента, при образовании трещин и опреде­ляемый по формуле:

,

где М_rp — момент усилия Р относительно той же оси, что и для определения М_r; знак момента определяется направлением вращения., т.е.

;

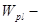упругопластический момент сопротивления железобетонного сечения по растянутой зоне в предположении, что продольная сила отсутствует;

– эксцентриситет усилия обжатия относительно центра тяжести приведенного сечения;

расстояние от ядровой точки, наиболее удаленной от растянутой зоны, до центра тяжести приведенного сечения.

 

Рис. 16.9. Схемы усилий напряжений в поперечном сечении элемента при расчете его по образованию трещин, нормальных к продольной оси элемента

а – при изгибе; б – при внецентренном сжатии; в – при внецентренном растяжении; г – при обжатии; 1 – ядровая точка; 2 – центр тяжести приведенного сечения

Поделиться:

Воспользуйтесь поиском по сайту: