 |
Теплообмен. Количество теплоты. Удельная теплоемкость. Уравнение теплового баланса.
|
|
|
|
Теплообмен - процесс изменения внутренней энергии без совершения телом работы ли самим телом.
Количество теплоты – это количественная мера изменения внутренней энергии тела при теплообмене. Измеряется в джоулях.
Удельная теплоемкость – это количество теплоты, которое необходимо сообщить телу массой 1 кг чтобы изменить его температуру на 1 К (1 °С).
Количество теплоты можно рассчитать:
1) Q = c∙m∙(T2-T1) = c∙m∙∆T – при нагревании или охлаждении; где Q – количество теплоты; с – удельная теплоемкость вещества, [c] =  ; m – масса тела; ∆T – изменение температуры. При нагревании тело получает энергию; при охлаждении – выделяет.
; m – масса тела; ∆T – изменение температуры. При нагревании тело получает энергию; при охлаждении – выделяет.
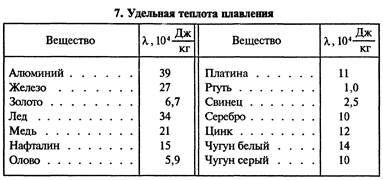
2) Q = λ∙m – при плавлении или кристаллизации, где λ – удельная теплота плавления [λ] = Дж/кг. При плавлении тело получает энергию, при кристаллизации – выделяет.
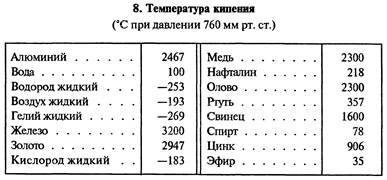
3) Q = r∙m – при парообразовании или конденсации; r – удельная теплота парообразования, [r] = Дж/кг. При парообразовании энергия поглощается телом, при конденсации – выделяется.
4) Q = q∙m – при сгорании вещества данное количество энергии выделяется веществом; q – удельная теплота сгорания топлива, [q] = Дж/кг.
Значения величин c, λ, r, q берут из соответствующих таблиц.
Если теплообмен происходит между несколькими телами, составляющими изолированную от окружающих тел систему, то применяют уравнение теплового баланса: Q1 + Q2 + … + Qn = 0
Уравнение теплового баланса справедливо для замкнутой системы (т. е. для достаточно изолированной от окружающих тел системы из-за чего ее внутренняя энергия не изменяется). Никакой работы внутри такой системы не совершается
∆U = Q + A, где А – работа внешних сил.
Поэтому, согласно первому закону термодинамики изменение энергии любого тела системы равно количеству теплоты отданной или полученной этим телом до наступления теплового равновесия внутри системы.
|
|
|
∆U = Qi
Складывая подобные выражения для всех тел системы и учитывая, что внутренняя энергия не меняется:
∆U1 + ∆U2 + … + ∆Un = 0, получим:
Q1 + Q2 + … + Qn = 0,
где Q1, Q2 – количество теплоты, полученное или отданное телами; n – число тел, участвующих в теплообмене.
Теплоту, полученную телом, считают положительной и в уравнении берут со знаком «+»; теплоту, отданную телом, считают отрицательной и ставят знак «-».
Уравнение теплового баланса первоначально было открыто при наблюдении теплообмена между телами в калориметре – приборе, максимально изолирующем систему тел от воздействия окружающей среды.
Алгоритм решения задач на уравнение теплового баланса:
1. Внимательно прочитать условие задачи, выяснить, сколько тел участвует в теплообмене и какие физические процессы происходят.
2. Кратко записать условие задачи, дополняя необходимыми табличными величинами.
3. Записать уравнение теплового баланса с учетом знака количества теплоты. Если тело получает энергию, то ставят знак «+», если отдает, то ставят знак «-».
4. Записать необходимые формулы для расчета количества теплоты.
5. Решить полученное уравнение в общем виде относительно искомых величин.
6. Произвести проверку размерности (единиц измерения) полученной величины.
7. Подставить исходные данные задачи и вычислить значения искомых величин.
Пример решения задачи на уравнение теплового баланса:
Задача: В латунный калориметр массой 150 г, содержащий 200 г воды при 15 °С, опустили железную гирю массой 260 г при температуре 100 °С. Определить общую установившуюся температуру. Потери тепла не учитывать.
| Дано: mk = 150 г = 0,15 кг mв = 200 г = 0,2 кг Тв = 288 К Тк = Тв mг = 260 г = 026 кг Tг = 373 К ск = 380 Дж/(кг∙К) св = 4200 Дж/(кг∙К) сг = 460 Дж/(кг∙К) Найти: Т -? | Решение:
В теплообмена участвуют три тела: калориметр, вода и железная гиря.
По таблицам определяем удельную теплоемкость латуни, воды и железа. Можно рассматривать эту систему как замкнутую.
Процессы:
1) Охлаждение железной гири: Qг = cг∙mг∙(Tг -T) – тепло отданное гирей
2) Нагревание воды: Qв = cв∙mв∙(T-Tв) – полученное количество тепла
3) Нагревание калориметра: Qк = cк∙mк∙(T-Tк) – полученное количество тепла
Запишем уравнение теплового баланса: Qк + Qв – Qг = 0
Подставим в уравнение выражение для количества теплоты:
cк∙mк∙(T-Tк) + cв∙mв∙(T-Tв) - cг∙mг∙(Tг -T) = 0
Из этого уравнения находим установившуюся температуру:
T = 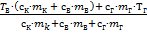 = 298 К = 25 °С = 298 К = 25 °С
|
|
|
|
Задачи: (при решении использовать формулы 1 – 4, а также вышеприведенный пример решения задачи на уравнение теплового баланса)
1. Кубики, изготовленные из алюминия и серебра массой 1 кг каждый, охлаждают на 1 °С. На сколько изменится внутренняя энергия каждого кубика.
2. Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж тепла. Чему равна теплоемкость камня? Удельная теплоемкость?
3. Кусок льда массой 0,8 кг нагревают от -20 °С до 0 °С. При этом затрачено количество теплоты 33,6 кДж. Определить теплоемкость куска льда в этом процессе и удельную теплоемкость льда, если плавление не происходит.
4. Сколько энергии пошло на нагревание от 20 °С до 920 °С железной заклепки, масса которой 110 г.
5. Какое количество теплоты пойдет на нагревание воды от 15 °С до 25 °С в бассейне, длина которого 100м, ширина 6 м и глубина 2 м?
6. На сколько градусов нагреется вода объемом 2 л, если ей сообщить количество теплоты 100 Дж.
7. При охлаждении куска олова массой 100 г до температуры 32 °С выделилось 5 кДж теплоты. Какой была температура олова до охлаждения?
8. На нагревание кирпича массой 4 кг на 63 °С затрачено такое же количество теплоты, как и для нагревания 4 кг воды на 13,2 °С. Сему равна удельная теплоемкость кирпича?
9. На какую высоту можно было бы поднять груз массой 2 т, если бы удалось полностью использовать энергию, освободившуюся при остывании стакана воды от температуры 100 °С до температуры 20 °С. Объем стакана 250 см3.
10. Какое количество льда, взятого при температуре плавления, можно растопить, затратив энергию 340 Дж?
|
|
|
11. Сколько теплоты уходит на приготовление воды из льда, масса которого 10 кг? Лед взят при температуре – 20 °С, а температура воды должна быть 15 °С.
12. Какое количество теплоты выделяется при конденсации водяного пара массой 2,5 кг, взятого при температуре кипения?
13. Какое количество теплоты необходимо для нагревания воды массой 10 кг от температуры 5 °С до 100 °С и превращения в пар ее части 0,4 кг?
Первый закон термодинамики:
Изменение внутренней энергии системы при переходе из одного состояния в другое равно сумме количества теплоты, сообщенного системе, и работы внешних сил, совершаемой над системой, то есть:
∆U = Q + A
Или: Количество теплоты, переданное системе, идет на изменение е внутренней энергии и на совершение системой работы над внешними телами:
Q = ∆U + A'
где Q – количество теплоты; ∆U – изменение или приращение внутренней энергии, А – работа внешних сил; А' – работа самой системы.
А = - А' = - p∙∆V, ∆V – изменение объема.
Процессы в газах в рамках первого закона термодинамики:
1. Изотермический процесс: (T = const): Внутренняя энергия не меняется: ∆U = 0 => Q = A.
Количество теплоты, сообщаемое системе, идет на совершение механической работы.
2. Изобарный процесс (p = const): В этом случае, если Q > 0, то газ и нагревается, и совершает механическую работу: Q = ∆U + A; A = p∙∆V.
3. Изохорный процесс (V = const): Механическая работа не совершается, так как ∆V = 0 => A = 0; следовательно, Q = ∆U, то есть количество теплоты идет на изменение внутренней энергии.
4. Адиабатный процесс – процесс, протекающий без теплообмена с окружающей средой: Q = 0. Следовательно, ∆U = A.
Задачи:
1. При изотермическом расширении идеальным газом совершена работа 15 кДж. Какое количество теплоты сообщено газу?
2. В закрытом баллоне находится газ. При охлаждении его внутренняя энергия уменьшилась на 500 Дж. Какое количество теплоты отдал газ? Совершил ли он работу?



|
|
|


