Явление электромагнитной индукции: Лабораторная работа №2-2 по общей физике / НГТУ; Сост.: Г.Д. Ботов и др. Заволжье, 2006.

Федеральное агентство по образованию

Государственное образовательное учреждение высшего

Профессионального образования

 

 

НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

 

 

Заволжский филиал

 

 

Кафедра общеобразовательных и общепрофессиональных дисциплин

 

Экспериментальное исследование электромагнитной индукции

 

 

Лабораторная работа №2-2 по общей физике

 

Заволжье – 2006

 

Составители: Г.Д. Ботов, Р.В. Бударагин

 

УДК 537.85

 

Явление электромагнитной индукции: Лабораторная работа №2-2 по общей физике / НГТУ; Сост.: Г.Д. Ботов и др. Заволжье, 2006.

 

 

Дано краткое описание явлений электромагнитной индукции (ЭМИ), само- и взаимоиндукции, рассмотрены процессы установления тока в LR-цепи. Представлена экспериментальная установка с использованием системы виртуальных измерений в среде LabVIEW по моделированию и изучению явления ЭМИ и порядок работы с ней.

 

Научный редактор Р.В. Бударагин

 

 

ВВЕДЕНИЕ

 

Явление электромагнитной индукции было открыто в 1831г. М. Фарадеем и нашло широкое техническое применение. Оно лежит в основе всей современной электро- и радиотехники. Благодаря элект­ромагнитной индукции, происходит переход механической энер­гии в электрическую и, наоборот, электрической в механическую; трансформаторы преобразуют низкое напряжение в высокое, и наобо­рот; возникают и распространяются радиоволны, свет, электромаг­нитные волны в различных линиях передачи. Переменные магнитные поля возбуждают в массивных проводниках индукционные токи Фуко, которые используются в металлургии для плавки металлов. Выход СВЧ-тока на поверхность проводника (скин-эффект), также связан­ный с ЭМИ, используется при поверхностной закалке деталей, его учитывают при конструировании СВЧ аппаратуры. В связи с этим экс­периментальное изучение ЭМИ представляет значительный интерес.

Целью данной работы является экспериментальное изучение явления ЭМИ, исследование зависимости тока от времени в LR -цепи при переходных процессах.

 

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

 

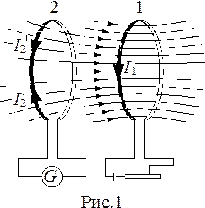1. Электромагнитная индукция. М. Фарадей обнаружил, что в замкнутом про­водящем контуре при изменении потока магнитной ин­дукции через поверхность, ограниченную этим контуром, возникает электрический ток (рис.1). Это явление называют электромагнитной индукцией, а возникающий ток – индукционным. Направление индукционного тока определяется правилом Ленца. Правило Ленца гласит, что магнитное поле, создаваемое индукционным током, направлено так, чтобы противодействовать изменению магнитного потока, его вызывающего.

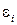Явление ЭМИ свидетельствует о том, что при изменениях магнитного потока в контуре возникает электродвижущая сила индукции , величина которой не зависит от способа, которым осуществля­ется изменение магнитного потока 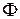, и определяется лишь скоростью изменения 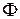, т. е. . При изменении знака направление 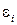также меняется (рис.2).

Возьмем виток проволоки площадью S и поместим этот виток во внешнее магнитное поле с индукцией (рис.3). Величина

(1)

называется потоком вектора магнитной индукции (магнитным потоком), пронизывающим виток. Вектор , называется вектором элементарной площадки, модуль которого равен dS, а направление совпадает с направлением нормали к площади dS.

Единицей потока магнитной индукции в СИ служит вебер (Вб), который представляет собой поток через поверхность в , пересекаемую нормальными к ней линиями магнитного поля с индукцией , равной 1 Тл.

При изменении магнитного потока со временем , величина ЭДС индукции наводимой в замкнутом контуре определяется

. (2)

Причем магнитный поток можно менять, изменяя во времени:

• магнитную индукцию внешнего магнитного поля;

• площадь замкнутого контура S;

• ориентацию контура относительно вектора магнитной индукции.

2. Самоиндукция. Рассмотрим виток проводящего провода, в котором течет ток I. Электрический ток, текущий в любом контуре, создает пронизывающий этот контур магнитный поток Ф. При изменениях I изменяется также и Ф, вследствие чего в контуре индуцируется ЭДС. Это явление называется самоиндукцией.

В соответствии с законом Био-Савара магнитная ин­дукция В пропорциональна силе тока, вызвавшего поле. Отсюда вытекает, что ток I в контуре и создаваемый им полный магнитный поток Ф через контур пропорциональны друг другу:

Ф = . (3)

Коэффициент пропорциональности L между силой тока и полным магнитным потоком называется и индуктивностью контура.

При неизменной силе тока I полный поток Ф может изменяться за счет изменений формы и размеров контура. Из сказанного следует, что индуктивность L зависит от геометрии контура (т. е. от его формы и размеров), а также от магнитных свойств (от ) окружающей контур среды.

3а единицу индуктивности в СИ принимается индук­тивность такого проводника, у которого при силе тока в нем 1 А возникает сцепленный с ним полный поток Ф, равный 1 Вб. Эту единицу называют генри (Гн).

Катушка индуктивности (соленоид) выполняется обычно медным проводом, навитым на круглый цилиндрический каркас, причем число витков и размеры проводника меняются в очень широких пределах.

Основным параметром катушки является индуктивность L, которая характеризует величину противоЭДС, наводимой (индуцируемой) в катушке при заданном изменении тока в ней.

Вычислим индуктивность соленоида длиной l, содержащего n витков площадью S. По определению:

(4)

где l – длинна магнитного пути (м), S – сечение этого пути (), 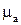– абсолютная магнитная проницаемость среды, в которой замыкается магнитный поток (принимаем за 1), – число витков катушки.

Т.о., индуктивность пропорциональна площади сечения витка катушки, числу витков катушки в квадрате и обратно пропорциональна магнитному сопротивлению пути, по которому замыкается магнитный поток, создаваемый током катушки.

3. Взаимная индукция. Рассмотрим 2 витка с токами и 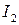(рис.4). Каждый ток будет создавать вокруг витков магнитное поле. Часть магнитного потока, создаваемого 1-м током, пронизывают нижний контур и наоборот. За величину обозначим часть магнитного потока 1 контура, который пронизывает 2 контур. За – часть магнитного потока 2 контура, который пронизывает 1 контур.

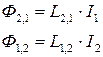. (5)

При изменениях тока в контуре 2 индуцируется ЭДС . Аналогично при протекании в контуре 2 тока силы 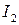в контуре 1 индуцируется ЭДС . Контуры 1 и 2 называются связанными, а явление возникновения ЭДС в одном из контуров при изменениях силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности и 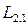называются взаимной индуктивностью контуров. В отсутствие ферромагнетиков они зависят от геометрической формы, размеров, взаимного расположения и магнитной проницаемости среды.

Вычислим взаимную индуктивность 2-х катушек, намотанных на общий тороидальный сердечник. Ток , текущий по катушке с количеством витков 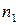, будет создавать в сердечнике магнитное поле В. Согласно закону полного тока:

. (6)

Т.о., полный поток, сцепленный с катушкой 2, имеющей витков: . Тогда взаимная индуктивность 2-х катушек определится, как

. (7)

Аналогично можно определить .

4. Процессы включения под напряжение и процессы короткого замыкания катушки индуктивности. Пусть в цепь с не зависящей от I индуктивностью L и сопротивлением R включен источник тока с ЭДС . Найдем характер изменения тока при замыкании цепи (ключ K в положении 1). После подключения источника ЭДС, до тех пор пока сила тока не достигнет установившегося значения, в цепи, кроме ЭДС , будет действовать ЭДС самоиндукции . В соответствии с законом Ома

. (8)

В последнем уравнении произведем замену , тогда . Уравнение (8) приобретает следующий вид 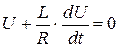. Последнее уравнение представляет собой линейное однородное дифференциальное уравнение первого порядка. Разделив переменные, решаем его методом интегрирования

. Отсюда ,

где С – постоянная интегрирования. Потенцирование этого соотношения дает

.

Значение постоянной интегрирования найдем из начальных условий. При сила тока в цепи , следовательно, . Окончательно получаем

, (9)

где – постоянная временицепи.

Постоянная времени цепи, измеряемая в секундах, зависит от индуктивности катушки L и эквивалентного омического сопротивления цепи R.

После подключения к цепи с катушкой постоянного напряжения ток в ней нарастает по экспоненциальному закону (рис.7). Так, за время, равное значению постоянной времени цепи, ток увеличится до 63% своего установившегося значения.

После приложения постоянного напряжения к цепи с катушкой спустя время падение напряжения на катушке уменьшается до 37 % его максимальной величины и после примерно (3... 4) достигает своего наименьшего значения, зависящего от омического сопротивления катушки.

Рассмотрим случай короткого замыкания катушки индуктивности. Пусть в цепь с не зависящей от I индуктивностью L и сопротивлением R включен источник тока с ЭДС (рис.8). В цепи будет течь постоянный ток (сопротивление источника тока считаем пре­небрежимо малым). В момент времени отключим источник тока, замкнув одновременно цепь накоротко ключом K (положение 2). Как только сила тока в цепи начнет убы­вать, возникнет ЭДС самоиндукции, проти­водействующая этому убыванию. Сила тока в цепи будет удовлетворять уравнению

. (10)

Уравнение (10) представляет собой линейное однородное дифференциальное уравнение первого порядка. Разделив переменные, решаем его методом интегрирования

. Отсюда ,

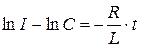где С – постоянная интегрирования. Потенцирование этого соотношения дает

.

Значение постоянной интегрирования найдем из начальных условий. При сила тока в цепи . Окончательно получаем

. (11)

При коротком замыкании катушки в ней наводится (индуктируется) ЭДС самоиндукции, которая имеет полярность, противоположную внешнему напряжению, и почти полностью затухает за время, равное (3...4) (рис.9).

Т.о., мгновенные значения тока и падения напряжения катушки при включении и при коротком замыкании катушки можно рассчитать, используя следующие формулы:

ток включения катушки под напряжение U

; (12)

падение напряжения на катушке при ее включении под напряжение U

; (13)

ток короткого замыкания катушки

; (14)

падение напряжения на катушке при ее коротком замыкании

. (15)

При всяком изменении тока в проводящем контуре возникает ЭДС самоиндукции, в результате чего в контуре появляются экстратоки самоиндукции. Исходя из правила Ленца, они всегда направлены так, что препятствуют изменению тока в цепи. Т.о., при замыкании цепи они препятствуют нарастанию тока, а при размыкании – его исчезновению.

 

МЕТОДИКА ЭКСПЕРИМЕНТА

 

Для исследования переходных процессов в -цепи используется модульный интегрированный учебный лабораторный комплекс, в состав которого входит блок маломощных генераторов напряжений специальной формы, измерительные трансформаторы тока и напряжения, набор резисторов и катушек индуктивности, которые конструктивно оформлены, как специальные моноблоки.

Блоки, входящие в аппаратную часть, размещаются на составном лабораторном столе с рамой и могут быть соединены в общую электрическую цепь с помощью защитных гнезд и гибких защищенных проводников.

Управление осуществляется персональным компьютером, оснащенным специальной платой ввода/вывода данных. Плата в сочетании с коннектором, блоком ввода/вывода цифровых сигналов и терминалом позволяет реализовывать виртуальное управление модулями, измерять и отображать параметры их режимов посредством виртуальных приборов и осциллографов.

 

Для исследования переходных процессов в -цепи с импульсного генератора на цепь (рис.10) подаются прямоугольные импульсы напряжения амплитудой и длительностью . В момент (передний фронт импульса) на -цепь "мгновенно" подается напряжение и держится пос­тоянным в течение длительности импульса . 3а это время проис­ходит нарастание тока в -цепи. В момент времени (задний фронт импульса) напряжение "мгновенно" снимает­ся, в результате происходит спад тока.

Вольтметр подключен ко всей -цепи и показывает напряжение, ко­торое подается с генератора. Виртуальные приборы и подключенные к виртуальному осциллографу, показывают форму напряжения на катушке индуктивности и значение силы тока от времени в -цепи, соответственно.

 

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

 

Проведение измерений.

• Соберите цепь согласно схеме (рис.10) и подсоедините к ее входным зажимам регулируемый источник напряжений специальной формы, настроенный на прямоугольные импульсы положительной полярности с параметрами: =6 В, f =250Гц (, , – соответствующие пары гнезд коннектора).

• Приведите компьютер в рабочее состояние и «подключите» два входа виртуального осциллографа к виртуальным приборам и ; настройте изображение.

• Выведите на дисплей виртуального осциллографа кривые тока и напряжения при подключении катушки индуктивности к постоянному напряжению и ее коротком замыкании.

• Воспроизведите осциллограммы на графике (рис.11)

 

Поделиться:

Воспользуйтесь поиском по сайту: