 |
Задачи уровня С5 предполагают не только получение результата, но и подробное описание хода решения.
|
|
|
|
Математика 11 класс - Практикум абитуриента
Марченко Любовь Васильевна, Костина Галина Викторовна, ДВГУПС (Хабаровск)
ГРАФИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ С ПАРАМЕТРАМИ
Задачи уровня С5 предполагают не только получение результата, но и подробное описание хода решения.
Пример 1. Построить на плоскости ХОУ множество точек, удовлетворяющих системе неравенств: 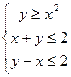 .
.
Решение. Границей области решения первого неравенства является парабола 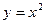 , а областью решения – точки, расположенные «выше» параболы. Границами областей решения двух других неравенств являются прямые x + y = 2 и х – y = 2, а областями решений – точки, расположенные «ниже» прямых. Область решения системы неравенств изображена на рисунке 1.
, а областью решения – точки, расположенные «выше» параболы. Границами областей решения двух других неравенств являются прямые x + y = 2 и х – y = 2, а областями решений – точки, расположенные «ниже» прямых. Область решения системы неравенств изображена на рисунке 1.
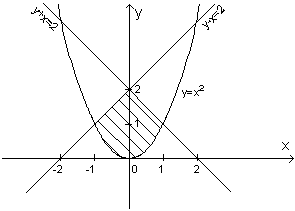
Рисунок 1
При построении рисунка желательно подписывать уравнения кривых.
Неравенства, входящие в систему, могут содержать знак модуля. Предполагается также, что учащиеся умеют строить график функции y=f(kx+b), если известен график функции y=f(x).
Каким же образом построение решения систем неравенств может помочь при решении задач с параметрами? Рассмотрим это подробнее на примерах заданий раздела С Единого Государственного Экзамена.
Пример 2 (задание С4, варианты 1-30, 2004 год ). Найдите все значения параметра а, при каждом из которых множество решений неравенства 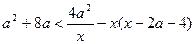 содержит какой-нибудь отрезок длины 2, но не содержит никакого отрезка длиной 3.
содержит какой-нибудь отрезок длины 2, но не содержит никакого отрезка длиной 3.
Решение. Поскольку неравенство содержит две переменные х и а, то его решение можно построить на плоскости в декартовой системе координат хоа (горизонтальная ось ох, вертикальная ось оа). Сразу можно отметить, что поскольку переменная х из неравенства находится в знаменателе, то 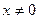 , то есть точки оси оа не являются решениями неравенства. Преобразуем неравенство к более удобному виду:
, то есть точки оси оа не являются решениями неравенства. Преобразуем неравенство к более удобному виду:
|
|
|
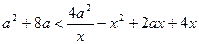 ,
, 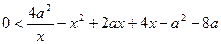 ,
,
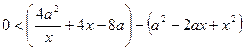 ,
, 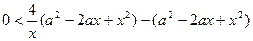 ,
,
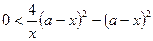 ,
, 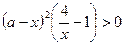 или
или 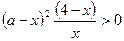 .
.
Поскольку 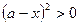 для всех действительных х и а, кроме х=а, то достаточно потребовать, чтобы
для всех действительных х и а, кроме х=а, то достаточно потребовать, чтобы 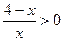 . Дробь положительна, если ее числитель и знаменатель одного и того же знака. Таким образом, полученное после преобразований неравенство равносильно двум системам неравенств:
. Дробь положительна, если ее числитель и знаменатель одного и того же знака. Таким образом, полученное после преобразований неравенство равносильно двум системам неравенств: 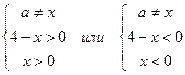 .
.
Вторая система не имеет решений, поскольку неравенства 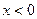 и
и 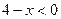 не могут выполняться одновременно.
не могут выполняться одновременно.
Для построения области решения первой системы неравенств изобразим на плоскости хоа прямые х=а, х=0 (ось оа), х =4. Все прямые (за исключением оси) изображаются пунктиром, поскольку неравенства, входящие в систему, строгие.
Областью решения исходного неравенства будет полоса 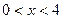 с вырезанной прямой
с вырезанной прямой 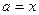 (рисунок 2).
(рисунок 2).
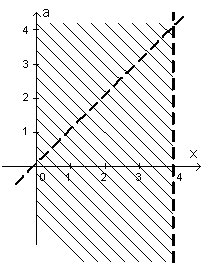
Рисунок 2
Для 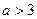 и
и 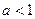 множество решений исходного неравенства относительно переменной х содержит отрезки длиной 3, поэтому требование задачи выполняется на промежутке от 1 до 3, причем значение параметра а= 2 исключается, так как при а =2 решение неравенства представляет собой два интервала длиной 2, но ни одного отрезка этой длины. Окончательно запишем, что при
множество решений исходного неравенства относительно переменной х содержит отрезки длиной 3, поэтому требование задачи выполняется на промежутке от 1 до 3, причем значение параметра а= 2 исключается, так как при а =2 решение неравенства представляет собой два интервала длиной 2, но ни одного отрезка этой длины. Окончательно запишем, что при  выполняются требования задачи.
выполняются требования задачи.
Пример 3 (задание С4, варианты 31-60, 2004 год). Найдите все значения параметра а, при каждом из которых множество решений неравенства 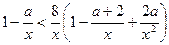 содержит какой-нибудь отрезок длиной 4 и при этом сам содержится в каком-нибудь отрезке длиной 7.
содержит какой-нибудь отрезок длиной 4 и при этом сам содержится в каком-нибудь отрезке длиной 7.
Решение. Преобразуем исходное неравенство:
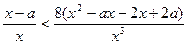 ,
, 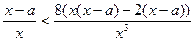 ,
,
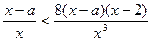 ,
, 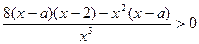 ,
, 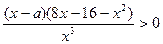 ,
,
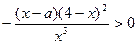 или
или 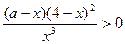 .
.
Поскольку 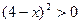 для всех действительных х, кроме х =4, а дробь положительна, если ее числитель и знаменатель одного знака, то неравенство равносильно двум системам неравенств:
для всех действительных х, кроме х =4, а дробь положительна, если ее числитель и знаменатель одного знака, то неравенство равносильно двум системам неравенств:
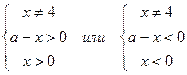 .
.
Границами решений этих неравенств на плоскости хоа являются прямые х=4, а-х=0, х=0 (ось оа). Поскольку неравенства строгие, то точки, принадлежащие указанным прямым, не являются решениями, поэтому прямые (за исключением оси оа) изображаются пунктиром. Подстановка координат произвольных точек позволяет заштриховать нужную часть плоскости, соответствующую множеству решений (рисунок 3).
|
|
|
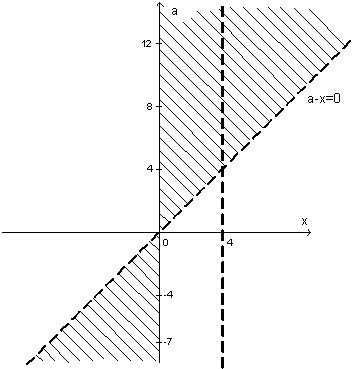
Рисунок 3
Теперь, используя полученный рисунок, выберем те значения параметра а, при которых множество значений х включает в себя отрезок длиной не менее 4 и не более 7. Это условие выполнятся для 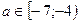 .
.
Следующий пример взят из статьи Б. Писаревского «Единый государственный экзамен по математике», опубликованной в журнале «Квант», №2, 2004 г.(с. 40-43). Как указано в публикации, пример относится к третьей части варианта ЕГЭ по математике 2003 года. Данный пример приведен в журнале с полным решением, полученным обычным аналитическим путем. Приводимое ниже решение, предлагаемое авторами данной статьи, использует графические построения.
Пример 4. Из области определения функции 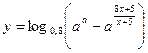 взяли все целые положительные числа и сложили их. Найдите все положительные значения а, при которых такая сумма будет больше 8, но меньше 15.
взяли все целые положительные числа и сложили их. Найдите все положительные значения а, при которых такая сумма будет больше 8, но меньше 15.
Решение. Согласно свойствам логарифмической функции, должно выполняться неравенство 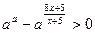 или
или 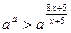 . Кроме того,
. Кроме того, 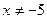 , поскольку выражение
, поскольку выражение 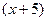 записано в знаменателе дроби, и из свойств показательной функции следует, что
записано в знаменателе дроби, и из свойств показательной функции следует, что 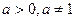 . Тогда выше приведенное неравенство выполняется в двух случаях:
. Тогда выше приведенное неравенство выполняется в двух случаях:
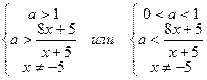 .
.
Линиями, определяющими границы области решений неравенств, являются прямые а =1, а =0 (горизонтальная ось ох) и гипербола 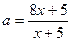 . Для удобства построения последней преобразуем правую часть и запишем
. Для удобства построения последней преобразуем правую часть и запишем 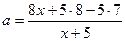 или
или 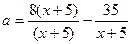 ,
, 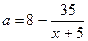 . Данную гиперболу удобно построить, заметив, что она получена параллельным переносом гиперболы
. Данную гиперболу удобно построить, заметив, что она получена параллельным переносом гиперболы 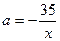 (перенос по вертикальной оси вверх на 8 единиц и по горизонтальной влево на 5 единиц).
(перенос по вертикальной оси вверх на 8 единиц и по горизонтальной влево на 5 единиц).
Все линии (за исключением координатной оси ох) изображаются пунктиром, поскольку неравенства строгие.
Область решения этих двух систем неравенств изображена на рисунке 4. Сразу можно заметить, что для 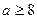 и
и 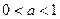 область определения функции содержит бесконечно много целых положительных чисел. Поэтому для указанных промежутков а условия задачи не выполняются. Следовательно, надо рассмотреть промежуток
область определения функции содержит бесконечно много целых положительных чисел. Поэтому для указанных промежутков а условия задачи не выполняются. Следовательно, надо рассмотреть промежуток 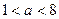 . Благодаря чертежу, можно сузить и этот промежуток, ограничившись значениями
. Благодаря чертежу, можно сузить и этот промежуток, ограничившись значениями 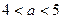 . Действительно, по мере возрастания параметра а от 1 до 8, количество целых положительных значений х, входящих в область определения увеличивается. Например, при
. Действительно, по мере возрастания параметра а от 1 до 8, количество целых положительных значений х, входящих в область определения увеличивается. Например, при 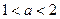 в область определения входит только одно целое положительное значение х =1, а для
в область определения входит только одно целое положительное значение х =1, а для 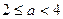 -- значения 1, 2, 3, сумма которых меньше 8. Для
-- значения 1, 2, 3, сумма которых меньше 8. Для 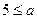 в область определения входят такие значения х, как 1, 2, 3, 4, 5, сумма которых равна 15, что не удовлетворяет требованиям задачи. Рассмотрим более подробно промежуток
в область определения входят такие значения х, как 1, 2, 3, 4, 5, сумма которых равна 15, что не удовлетворяет требованиям задачи. Рассмотрим более подробно промежуток 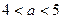 . Нас интересуют такие значения параметра а, при которых в область определения функции будут попадать значения 1, 2, 3, 4, но не попадет значение х =5. Границей области решения неравенства является гипербола
. Нас интересуют такие значения параметра а, при которых в область определения функции будут попадать значения 1, 2, 3, 4, но не попадет значение х =5. Границей области решения неравенства является гипербола 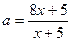 , в уравнение которой мы и подставим значения х =4 и х =5. При х =4, получим
, в уравнение которой мы и подставим значения х =4 и х =5. При х =4, получим 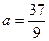 , а для х =5 получим
, а для х =5 получим 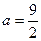 . Таким образом, условия задачи выполняются при
. Таким образом, условия задачи выполняются при 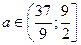 .
.
|
|
|

Рисунок 4.
Предлагаемый способ решения не является универсальным, а лишь одним из возможных.
Действительно, в выше приведенных примерах чертеж помогал в выборе решения. Но иногда подсказки рисунка бывает недостаточно, и приходится проводить еще и аналитические рассуждения. Так, при решении примера С4 (варианты 61-90. 2004 год), аналитическая часть оказалась весьма существенной. Приведем краткое изложение решения без подробного описания построения кривых. Авторы полагают, что в данном конкретном примере графическое решение оказалось не столь очевидным в сравнении с выше приведенными задачами, хотя оно и позволило облегчить поиск решения.
Пример 5 (задание С4, варианты 61-90, 2004 год). Найдите все положительные значения параметра а, при каждом из которых множество решений неравенства 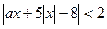 содержится в некотором отрезке длиной 10 и при этом содержит какой-нибудь отрезок длиной 2.
содержится в некотором отрезке длиной 10 и при этом содержит какой-нибудь отрезок длиной 2.
Решение. Запишем исходное неравенство в виде двойного неравенства 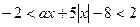 или
или 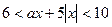 . Рассмотрим следующие случаи.
. Рассмотрим следующие случаи.
1 случай. Если 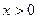 , то
, то 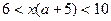 . Так как по условию
. Так как по условию  , то
, то 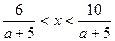 . Графиками функций
. Графиками функций 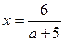 и
и 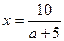 являются гиперболы с асимптотами
являются гиперболы с асимптотами 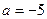 и х =0. Построим ветви гипербол, соответствующие значениям
и х =0. Построим ветви гипербол, соответствующие значениям  . Множество точек, удовлетворяющих неравенству
. Множество точек, удовлетворяющих неравенству 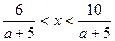 , находятся между ветвями гипербол (рисунок 5).
, находятся между ветвями гипербол (рисунок 5).
|
|
|
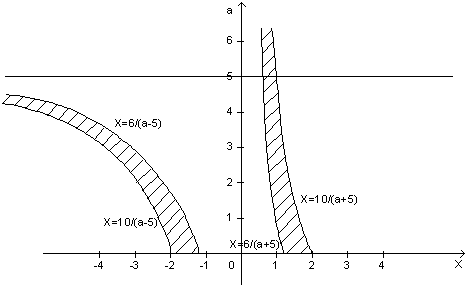
Рисунок 5
2 случай. Если 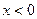 и
и 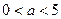 , то
, то 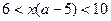 или.
или. 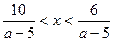 . (При
. (При 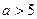 неравенство не имеет смысла, так как рассматриваем случай
неравенство не имеет смысла, так как рассматриваем случай 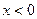 .) Построим ветви гипербол
.) Построим ветви гипербол 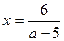 и
и 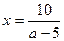 , соответствующие значениям
, соответствующие значениям 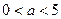 и
и 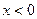 . Множество точек, удовлетворяющих неравенству
. Множество точек, удовлетворяющих неравенству 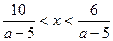 , находится между ветвями гипербол.. Из чертежа видно, что отрезок длиной 2 может находиться только между ветвями гипербол
, находится между ветвями гипербол.. Из чертежа видно, что отрезок длиной 2 может находиться только между ветвями гипербол 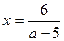 и
и 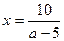 , то есть
, то есть 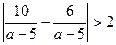 или
или 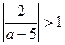 . Отсюда
. Отсюда 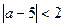 ,
, 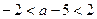 ,
, 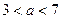 . С учетом того, что
. С учетом того, что 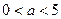 , получим
, получим 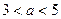 . Но, так как решения исходного неравенства должны содержаться в отрезке длиной 10, то
. Но, так как решения исходного неравенства должны содержаться в отрезке длиной 10, то 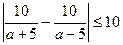 или
или 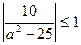 . Решая полученное неравенство, придем к соотношению:
. Решая полученное неравенство, придем к соотношению: 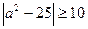 , откуда
, откуда
 .
.
Учитывая, что 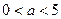 , получим
, получим 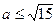 . Объединяя два множества
. Объединяя два множества 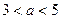 и
и 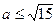 , делаем вывод, что при
, делаем вывод, что при 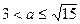 множество решений неравенства
множество решений неравенства 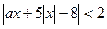 содержится в некотором отрезке длиной 10 и при этом содержит какой-нибудь отрезок длиной 2.
содержится в некотором отрезке длиной 10 и при этом содержит какой-нибудь отрезок длиной 2.
Авторы надеются, что предложенный в данной статье метод решения поможет при решении задач с параметрами. Все замечания и добавления по данному вопросу будут с благодарностью приняты.
|
|
|


