 |
Числовая функция. Область определения. Множество значений. Способы задания функции.
|
|
|
|
Функция – зависимость переменной У от переменной Х если каждому значению Х соответствует единственное значение У.
Переменная Х - независимая переменная(аргумент). Переменная У зависимая переменная.
Область определения функции - все значения, которые принимает независимая переменная.
Область значений функции ( множество значений)- все значения, которые принимает функция.
Способы задания функции
Словесный (С помощью естественного языка)
Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями.
Н-р: Игрек равно целая часть от икс.
Аналитический способ (С помощью формулы и стандартных обозначений)
Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно кусочное задание, то есть различное для различных значений аргумента.
Н-р: F(x)= 
Графический (С помощью графика)
Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены.
Н-р:

Y=arctg x
Табличный (С помощью таблицы значений)
Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов
|
|
|
Н-р:
x 0 1 2 3 4 y 1 1 2 3 5
25. Свойства функции. ( монотонность, знакопостоянство, четность)
Функция которая только возрастает или только убывает называется монотоннной.
Возрастающая функция- если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)<f(х2)
Убывающая функция- если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)>f(х2)
Возрастающая функция(в некотором промежутке) – функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) – функция у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Промежутки знакопостоянства
Промежутки знакопостоянства – такие множества значений аргумента на которых значения функции только положительны или только отрицательны.
Четность\нечетность.
Функция является четной- если для любого х из области определения функции выполняется равенство f(x)=f(-x)
Функция является нечетной- если для любого х из области определения функции выполняется равенство f(-x)= - f(x)
26. Прямая пропорциональность - функция, заданная формулой у=kx, где к(0. Число k называется коэффициентом пропорциональности.
Cвойства функции y=kx:
1. Область определения функции- множество всех действительных чисел
2. y=kx - нечетная функция
3. При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой

27.Обратная пропорциональность - функция, заданная формулой y=k/х, где k(0 Число k называют коэффициентом обратной пропорциональности.
Свойства функции y=k/x:
1. Область определения- множество всех действительных чисел кроме нуля
2. y=k/x- нечетная функция
3. Если k>0, то функция убывает на промежутке (0;+() и на промежутке (-(;0). Если k<0, то функция возрастает на промежутке (-(;0) и на промежутке (0;+().
|
|
|
Графиком функции является гипербола. 
28.Линейная функция - функция, которая задана формулой y=kx+b, где k и b-действительные числа. Если в частности, k=0, то получаем постоянную функцию y=b; если b=0, то получаем прямую пропорциональность y=kx.
Свойства функции y=kx+b:
1. Область определения- множество всех действительных чисел
2. Функция y=kx+b общего вида, т.е. ни чётна, ни нечётна.
3. При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой
Графиком функции является прямая. График функции y = kx + b получается сдвигом графика функции y = kx на b единиц вдоль оси ординат. Графиками функций y = kx и y = kx + b являются параллельные прямые.
КВАДРАТИЧНАЯ ФУНКЦИЯ
y = a  + bx + c, где a
+ bx + c, где a  0.
0.
График квадратичной функции - парабола.
Свойства функции и вид её графика определяются, в основном, значениями коэффициента a и дискриминанта D = b2 - 4ac.

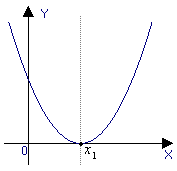
a > 0, D > 0 a > 0, D = 0


a > 0, D < 0 a < 0, D > 0


a < 0, D = 0 a < 0, D < 0
РАЗЛИЧНЫЕ ПРЕДСТАВЛЕНИЯ КВАДРАТИЧНОЙ ФУНКЦИИ
ВЫДЕЛЕНИЕ ПОЛНОГО КВАДРАТА:

РАЗЛОЖЕНИЕ НА ЛИНЕЙНЫЕ МНОЖИТЕЛИ
при D > 0 y = ax2 + bx + c = a(x - x1)(x - x2)
при D = 0 y = ax2 + bx + c = a(x - x1)2
при D < 0: разложить на множители нельзя.
Свойства:
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ: R
ОБЛАСТЬ ЗНАЧЕНИЙ:
при a > 0 [-D/(4a);)
при a < 0 (-;-D/(4a)]
ЧЕТНОСТЬ, НЕЧЕТНОСТЬ:
при b = 0, то функция четная
при b 0, то функция ни четная, ни нечетная
НУЛИ:
при D > 0 два нуля:
при D = 0 один нуль: x1 = -b/(2a)
при D < 0 нулей нет
ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА:

если a > 0, D = 0, то y > 0 при x (-;x1)U(x1;)
если a > 0, D < 0, то y > 0 при x R

если a < 0, D = 0, то y < 0 при x (-;x1)U(x1;)
если a < 0, D < 0, то y < 0 при x R
ПРОМЕЖУТКИ МОНОТОННОСТИ:


|
|
|


