 |
Краткая теоретическая часть
|
|
|
|
Теплоёмкость.
Отношение теплоты δq, полученной единицей количества вещества к изменению температуры dt называют удельной теплоемкостью.
 (1.1)
(1.1)
Поскольку количество теплоты δq зависит от характера процесса, то и теплоемкость системы CX также зависит от условий протекания процесса.
Теплоемкость в зависимости от количества вещества может быть массовой – С, объемной – С' и мольной µC. Связь между ними:
 (1.2)
(1.2)
Физический смысл теплоемкостей идеального вещества при V = const и P = const следует из рассмотрения дифференциальных соотношений термодинамики вида:
 (1.3)
(1.3)
После соответствующих преобразований с учётом свойств идеального газа получим:
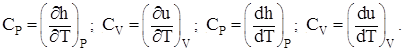 (1.4)
(1.4)
Это свидетельствует о том, что изменения внутренней энергии и энтальпии определяются как:
 (1.5)
(1.5)
т.е. независимо от характера процесса.
Соотношения между CP и CV:
 (1.6)
(1.6)
В соответствии с молекулярно-кинетической теорией газов мольная теплоемкость при V = Const пропорциональна числу их степеней свободы, выраженному в джоулевом эквиваленте и для одного моля газа равна µСV = 3 × 4,19 = 12,5 Дж/(моль×К). Тогда в соответствии с законом Майера, µСP = 5 × 4,19 = 20,8 Дж/(моль×К), что позволяет в зависимости от атомности газа и их степеней свободы представить значения мольных теплоёмкостей в следующем виде:
Таблица № 1.1.
| Атомность газа | μCV | μCP | ||
| Дж/(моль×К) | кал/(моль×К) | Дж/(моль×К) | кал/(моль×К) | |
| одноатомный | 12,5 | 3 | 20,8 | 5 |
| двухатомный | 20,8 | 5 | 29,1 | 7 |
| трёх - и более атомный | 29,1 | 7 | 37,4 | 9 |
Теплоемкость, определяемая по уравнению (4.1) при заданных параметрах состояния (P, v, Т) называемая истинной и может быть выражена как:
CX = CX0 + ΔCX,(1.7)
где СX0 – теплоемкость газа в разряженном состоянии (при P " 0) и зависит только от температуры, а ΔСX – определяет зависимость теплоемкости от давления и объема.
|
|
|
Средняя теплоемкость СXm в интервале температур от T1 до T2 выражается как:
 (1.8)
(1.8)
Если принять что один из пределов, например T1 = 273,15 К, то можно рассчитать средние теплоемкости газов в интервале температур от t1 = 0 °C до t2 = х °C и представить их значения в табличной форме, см. приложение, таблицы №2 – №4.
Количество теплоты, передаваемое системе согласно уравнению (4.8) и используя данные теплоемкостей, таблицы №2 – №4, с учетом (4.2), в зависимости от процесса рассчитывается по формулам:
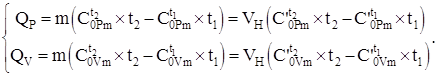 (1.9)
(1.9)
Для приближенных расчетов количества теплоты при не очень высоких температурах можно принять C = Const и тогда уравнения (1.14) с учетом (1.2) – (1.4) и значений таблицы №4.1. будут иметь вид:
 (1.15)
(1.15)
Задачи для самостоятельного решения.
Задача № 1-1. Воздух имеющий объем V = 15 м3 при температуре t1 = = 1500 °C и давлении Р = 760 ммHg, охлаждается изобарически до температуры t2 = 250 °C. Определить отводимое тепло QP, если: а) считать теплоемкость постоянной, б) использовать формулу µСP = 6,949 + + 0,000576×t.
Задача № 1-2. Расход воздуха измеряется с помощью электрического нагревателя, установленного в воздухопроводе. Температура воздуха перед нагревателем и за ним измеряется с помощью двух термометров. Определить часовой расход воздуха G кг/ч, если при включении электрического нагревателя мощностью 0,75 кВт температура воздуха перед нагревателем Т1 = 288 К, а за нагревателем Т2 = 291,1 К. Определить также скорость потока воздуха за нагревателем, если давление его (принимаемое нами неизменным) Р = 870 ммHg, а диаметр воздухопровода d = 90 мм.
Задача № 1-3. В результате полного сгорания углерода в атмосфере чистого кислорода в сосуде образовался углекислый газ СО2 при давлении Р = 6,04 бар и температуре Т1 = 1673 К. Какое количество тепла выделится при остывании СО2 до температуры Т2 = 293 К. Определить также, какое давление установиться при этом в сосуде и какое давление имел кислород в сосуде до сгорания, если температура его равнялась 10 °C. Объем сосуда принять неизменным и равным 5 литров.
|
|
|
Задача № 1-4. Найти количество тепла, необходимое для нагревания 1 нм3 газовой смеси состава τ(CO2) = 14,5%; τ(O2) = 6,5%; τ(N2) = 79,0% от 200 до 1200 °C при P = Const и нелинейной зависимости теплоемкости от температуры.
Пример. Воздух в количестве 6 м3 при давлении Р1 = 3 бар и температуре t1 = 25 °C нагревается в процессе P = Const до t2 = 130 °C. Определить количество подведенного тепла, считая С = Const и С = f(T).
Решение.
QP = m × CP × (t2 – t1) = VН × C'P × (t2 – t1);
QP = m × (CPm × t2 – CPm × t1) = VН × (C'Pm × t2 – C'Pm × t1).
m = (Р1 × V1 × µ) /(R × T1) = (3×105 × 6 × 2,896×10–2) /(8,314 × 298,15) = 21,03 кг.
VН = (Р1 × V1 × TН) /(РН × T1) = (3×105 × 6 × 273,15) /(101325 Па × 298,15) = 16,28 нм3.
QP = 21,03 × (29,33/2,896 × 10–2) × (130 – 25) = 16,28 × (29,33/2,24 × 10–2) × (130 – 25) = 2236,4 кДж.
QP = 21,03 кг × (1,0079 × 130 – 1,0042 × 25) = 16,28 × (1,3026 × 130 – 1,298 × 25) = 2227,5 кДж.
Расхождение 0,40%.
Задача № 1-5. В закрытом сосуде ёмкостью V = 0,5 м5 содержится диоксид углерода при Р = 6 бар и Т = 800 К. Как изменится давление газа, если от него отнять 100 ккал? Принять зависимость C = f(T) линейной.
Задача № 1-6. Сосуд емкостью 90 л содержит воздух при давлении 8 бар и температуре 303 К. Определить количество тепла, которое необходимо сообщить воздуху, чтобы повысить его давление при V = Const до 16 бар. Принять зависимость C = f(T) нелинейной. Ответ дать в ккал.
Задача № 1-7. Какое количество тепла необходимо затратить, чтобы нагреть 2 м3 воздуха при постоянном избыточном давлении РМ = 2 бар от t1 = 100 °C до t2 = 500 °C? какую работу при этом совершит воздух? Давление воздуха по барометру принять равным 760 ммHg.
Задача № 1-8. При изобарическом нагревании от Т1 = 313 К до Т2 = 1023 К однородный газ совершает работу l = 184 кДж/кг. Определить, какой это газ, какое количество тепла ему сообщено и как при этом изменилось его давление.
Задача № 1-9. В процессе подвода тепла при постоянном давлении температура 0,9 нм3 азота повышается от Т1 = 288 К до Т2 = 1873 К. Определить изменения энтальпии азота и долю тепла, пошедшую на увеличение внутренней энергии.
Задача № 1-10. В цилиндре с подвижным поршнем заключен кислород в количестве VН = 0,3 нм3 при Т1 = 318 К и Р1 = 776 ммHg. Некоторое количество тепла сообщается кислороду при Р = Const, а затем производится охлаждение до начальной температуры (318 К) при V = Const. Определить количество подведенного тепла, изменения энтальпии, внутренней энергии и произведенную работу для обоих процессов, если известно, что в конце изохорического охлаждения давление кислорода Р3 = 0,588 бар. Изобразите состояния газа в P – V и T – S координатах.
|
|
|
|
|
|
12 |


