Поле равномерно заряженной плоскости.

Теорема Гаусса.

Потоком вектора напряженности электрического поля называется скалярная физическая величина, равная скалярному произведению:

(1.11) или

(1.12)

В формуле (1.12) - угол между направлением вектора напряженности электрического поля и нормалью к плоскости .

 

Основная теорема электростатики.

Поток вектора напряженности электростатического поля сквозь любую замкнутую поверхность пропорционален заряду, заключенному внутри этой поверхности. Коэффициент пропорциональности .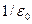

(1.13)

Формула (1,13) справедлива, если заряды дискретны. Если заряд равномерно распределен по объему тела:

(1.13’),

где ρ – объемная плотность электрического заряда.

Потенциал электростатического поля в вакууме.

Разность потенциалов.

Пусть заряд q перемещается в поле из точки 1 в точку 2. Работа, которая совершается зарядом, определяется как скалярное произведение силы на перемещение.

(1.20),

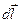где - проекция вектора на перемещение . Эта работа зависит только от положения начальной и конечной точки и не зависит от траектории перемещения, следовательно, электростатические силы – консервативные силы, а электростатическое поле является потенциальным. Для заряда q= 1

(1.21) –

разность потенциалов между точками 1 и 2. Разность потенциалов – работа по перемещению единичного положительного заряда из точки 1 в точку 2 силами электростатического поля, и называются потенциалами начальной и конечной точек траектории. Если рассматривать бесконечно удаленную точку, потенциал которой равен нулю, то потенциал - работа, совершаемая силами поля при перемещении единичного положительного заряда из данной точки поля в бесконечность.

(1.22),

То есть потенциал данной точки поля есть потенциальная энергия единичного положительного заряда, помещенного в данную точку поля. Рассмотрим работу А, совершаемую при перемещении заряда q по замкнутой траектории. Интеграл

называется циркуляцией вектора E по замкнутому контуру. Таким образом, циркуляция по замкнутому контуру равна нулю. Это означает, что в электростатическом поле нет замкнутых линий напряженности. Они начинаются и заканчиваются на электрических зарядах и уходят в бесконечность. Таким образом, электростатическое поле является безвихревым. В электростатическом поле можно построить поверхности с одинаковым потенциалом. Эти поверхности называются эквипотенциальными. Тогда при движении заряда по такой поверхности

(1.23)

Если и , то точка движется по эквипотенциальной поверхности под углом 90⁰. Линии напряженности электростатического поля всегда перпендикулярны эквипотенциальным поверхностям. Напряженность поля:

или 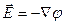(1.24)

Знак минус означает, что напряженность всегда направлена в сторону убывания потенциала.

(1.25)

 

Потенциалы некоторых полей.

Поле точечного заряда.

Потенциал поля заряженного проводящего шара. Так как внутри шара напряженность отсутствует, то вне шара напряженность вычисляется как для точечного заряда. Потенциал внутри шара:

Поле равномерно заряженной плоскости.

 

Проводники во внешнем электрическом поле.

Опыт Кавендиша. Заряженный шарик подвешивали на нити и поместили внутрь другого шара. Заряженный шар, подвешенный на диэлектрической нити, помещался внутрь незаряженной сферы, составленной из двух полусфер, находящихся на изолированной подставке. Внутренний шар соединили тонкой проволокой со сферой. В опыте было установлено, что весь заряд с шара перетекал на поверхность сферы. Вывод: таким образом, заряд всегда распределяется по поверхности проводника.

Внесем заряд во внешнее электрическое поле, например, пространство между пластинами конденсатора. Проводник представляет собой два шарика, соединенные тонкой проволокой. При помещении проводника в электрическое поле искажаются силовые линии электрического поля. Так как линии поля не перпендикулярны поверхности проводника, начинается перемещение заряда до тех пор, пока индуцированное электрическое поле не скомпенсирует поле внутри проводника, а вне проводника силовые линии не станут перпендикулярны его поверхности. При этом проводник приобретает постоянный потенциал. Если разделить проводник на две части, то обе части окажутся заряженными противоположными знаками. Если их снова соединить, то проводник окажется вновь незаряженным. Это говорит о том, что заряды возникают противоположного знака в равных количествах. Это явление называется явлением электростатической индукции. Если проводник, вносимый в электрическое поле, имел заряд, то этот заряд также перераспределяется до тех пор, пока не выровняется потенциал. Если заряженный проводник внести внутрь незаряженного проводника, то на внутренней поверхности этого проводника индуцируется заряд –q, а на внешней поверхности +q. Если проводники коснутся, то весь заряд распределится по поверхности проводника.

 

Диэлектрики в электрическом поле.

Диэлектрики – вещества, в которых отсутствуют свободные носители электрических зарядов. Молекулы в целом являются электрически нейтральными. Все диэлектрики можно условно разделить на несколько групп.

К первой группе относят вещества, имеющие симметричное строение – центр тяжести положительных и отрицательных зарядов совпадают. Неполярные диэлектрики. Под действием электрического поля электрические заряды в молекуле размещаются в противоположные стороны: положительные по полю, отрицательные протии поля. При этом молекулы приобретают дипольный момент.

Ко второй группе относятся диэлектрики, молекулы которых имеют ассиметричное строение, то есть центры тяжести положительных и отрицательных зарядов пространственно разделены. Такие молекулы даже в отсутствии внешнего электрического поля обладают дипольным моментом. Из-за хаотического дипольного движения молекул, эти дипольные моменты распределены случайным образом и следовательно, суммарный дипольный момент любого макроскопического объема равен нулю.

К третьей группе относят вещества, которые представляют собой ионные кристаллы, то есть правильное чередование положительных и отрицательных зарядов. Кристаллическую решетку таких веществ можно представить как две подрешетки из положительных и отрицательных ионов, вставленных друг в друга. При помещении такого кристалла в электрическое поле происходит некоторая деформация кристаллической решетки, в результате которой две подрешетки смещаются друг относительно друга и макроскопический объем кристалла приобретает дипольный момент.

Поляризацией диэлектриков называется процесс появления ориентированных диполей под действием внешнего электростатического поля. Деформационная поляризация заключается в возникновении у атомов индуцированного дипольного момента за счет деформации молекул (у неполярных диэлектриков). Ориентационная поляризация возникает в полярных диэлектриках и заключается в том, что под действием электрического поля, молекулы полярного диэлектрика ориентируются таким образом, что макроскопический объем приобретает дипольный момент.

Ионная поляризация имеет место в ионных кристаллах и заключается в деформации кристаллической решетки, приводящей к появлению дипольного момента.

Вектор поляризации p или поляризованность вещества это дипольный момент единицы объема вещества:

(1.26)

- дипольный момент отдельных молекул

- объем вещества

В формуле (1.26) суммирование производится по всем дипольным моментам, заключенным в выбранном объеме.

Для большинства диэлектриков вектор поляризации пропорционален напряженности электрического поля

(1.27)

где - электрическая постоянная, а - диэлектрическая восприимчивость вещества:

На поверхности диэлектриков, внесенных в электрическое поле, «обнажаются» связанные заряды и появляется собственное электрическое поле, всегда направленное навстречу внешнему. Таким образом, напряженность электрического поля в диэлектрике оказывается меньше напряженности внешнего поля.

(1.28)

(1.29)

Поле, созданное связанными зарядами: ; , откуда напряженность результирующего поля внутри диэлектрика равна:

(1.30)

Физическая величина , которая показывает, во сколько раз напряженность электрического поля в диэлектрике меньше, чем напряженность внешнего электрического поля, называется диэлектрической проницаемостью диэлектрика.

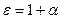(1.31)

 

Теорема Гаусса для поля в веществе.

Вектор электростатического смещения. Для характеристики электростатического поля в веществе вводят так называемый вектор электростатического смещения D, который учитывает не только свободные, но и связанные заряды, возникающие в диэлектрике под действием электрического поля.

(1.32)

Вектор электростатического смещения является силовой характеристикой поля, так как определяется силой, действующей на единичный положительный заряд. Вектор электростатического смещения не имеет смысла, как силовая характеристика поля. Это расчетная величина, которая позволяет учесть наличие связанных зарядов в диэлектрике и упростить выражение теоремы Гаусса для диэлектриков:

(1.33)

Поток вектора электростатического смещения сквозь замкнутую поверхность равен сумме свободных зарядов, заключенных внутри этой поверхности.

 

Граничные условия на границе двух диэлектриков.

Предположим, что имеется два диэлектрика с диэлектрической проницаемостью 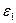и , разделенных плоской границей и находящихся в постоянном электрическом поле с напряженностью Е.

Циркуляция вектора напряженности. Введем на границе раздела диэлектриков замкнутый контур 1234, стороны которого 23 и 41 можно сделать сколь угодно малыми.

Согласно теореме о циркуляции вектора Е,

, откуда .

Поэтому

(1.34)

На границе раздела двух диэлектриков линии напряженности электростатического поля непрерывны из равенства (1.34), а линии электростатического смещения терпят разрыв. Тангенциальная составляющая вектора напряженности электрического поля непрерывна, а вектор электрического поля неразрывны, а векторы электрического смещения терпит разрыв. Предположим, что на границе раздела двух сред нет свободных зарядов. Выделим на границе раздела прямоугольный параллелепипед, высоту которого можно сделать сколь угодно малой. Согласно теореме Гаусса для поля в веществе

, откуда (1.35)

Заменив проекции вектора D проекциями вектора E, умноженными на , получим:

(1.36)

На границе раздела двух сред нормальные составляющая вектора электрического смещения непрерывны, а нормальные составляющие вектора напряженности электрического поля терпят разрыв.

 

Электроемкость уединенного проводника.

Проводник называется уединенным, если вблизи него нет других проводящих тел и зарядов. Сообщая проводнику какой-либо заряд, мы изменяем его потенциал. Известно, что между сообщенным зарядом и потенциалом проводника существует прямая зависимость:

(2.1)

С – коэффициент пропорциональности, называется электроемкостью проводника. Электроемкость проводника численно равна заряду, изменяющему потенциал проводника на один вольт. Единица электроемкости – «фарад» 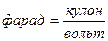. Электроемкость проводника не зависит от заряда и потенциала, а определяется только геометрическими размерами проводника, а также электрическими свойствами среды, в которой находится проводник.

Примеры:

- емкость медного шара равна емкости алюминиевого;

- емкость сплошного шара равна емкости полой сферы;

- емкость твердого шара равна емкости жидкого шара (ртути);

при тех же размерах и тех же свойствах среды.

 

Энергия уединенного проводника.

Пусть имеется уединенный проводник емкостью С, заряженный зарядом q до потенциала . Сообщим ему дополнительный заряд 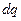, перенеся его из бесконечности. При этом мы совершим работу против сил электростатического отталкивания, которая по закону сохранения энергии превратится в приращение энергии проводника.

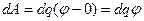
(2.1)

(2.2)

Таким образом, для того, чтобы зарядить незаряженный проводник зарядом q до потенциала , нужно совершить работу А согласно формуле (2.1), при этом уединенный проводник получает энергию согласно формуле (2.2). Энергия системы проводников является аддитивной величиной и равна сумме энергий всех тел, составляющих систему.

 

Задачи на соединение заряженных проводников.

При соединении заряженных проводников их потенциалы выравниваются, а заряды перераспределяются в зависимости от емкости таким образом, что выполняется закон сохранения электрического заряда. Предположим, что имеются два проводника, емкости которых С₁ и С₂ с потенциалами и , при соединении этих проводников (их заряды и ) потенциалы выравниваются, а заряды перераспределяются. Из закона сохранения заряда следует, что .

При внесении одного проводника внутрь другого, заряд распределяется по поверхности внешнего проводника, а потенциалы проводников выравниваются.

При соединении проводников проскакивает искра и выделяется тепло. То есть, потенциальная энергия системы проводников изменяется. До соединения было:

Примечание: при соединении жидких проводников, например, капель ртути на баланс энергии существенно влияет состояние свободной поверхности проводников.

 

Конденсаторы.

Накапливать заряды на поверхности уединенного проводника невыгодно, так как увеличении емкости приводит к увеличению размера проводника. поэтому используют конденсатор. Если к заряженному проводнику поднести какое-либо тело, то в этом теле под действием поля возникают свободные или связанные в диэлектрике заряды. Вблизи заряженного проводника ближайшими к проводнику окажутся заряды противоположного знака. Их поле будет понижать потенциал проводника, и, следовательно, чтобы изменить потенциал на один вольт потребуется больший заряд, то есть емкость такой системы возрастает.

Конденсаторы это устройства, состоящие из двух проводников, отделенных слоем диэлектрика. По конструкции конденсаторы изготавливают таким образом, чтобы все поле было сосредоточено между обкладками конденсатора. Тогда на емкость конденсатора не будут влиять окружающие тела. В зависимости от формы обкладок, конденсаторы бывают плоскими (состоящими из двух пластин), сферическими (состоящими из двух концентрических сфер), цилиндрические (состоящие из двух цилиндров, имеющих общую ось). Так как все поле сосредоточено между обкладками конденсатора, то все силовые линии начинаются на положительных и заканчиваются на отрицательных зарядах. Так как все силовые линии электрического поля начинаются заканчиваются только на зарядах, то это означает, что абсолютная величина заряда на обеих обкладках будет одинакова. Емкостью конденсатора называется отношение заряда на одной из обкладок к напряжению между обкладками:

(2.4)

 

Конденсаторные батареи.

Предположим, что конденсаторы соединены таким образом, что напряжение на обоих конденсаторах одинаково. При этом заряды на батареях конденсаторов являются суммой зарядов на каждом конденсаторе в отдельности. Такое соединение называется параллельным соединением конденсаторов.

(2.5)

(2.6)

Т.к. , то

(2.7)

Последовательное соединение называется такое соединение конденсаторов, при котором заряд на каждом конденсаторе и q на всей батарее конденсаторов одинаков, а напряжение складывается.

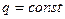(2.8)

(2.9)

 

Частные случаи.

Соединение двух конденсаторов:

Соединение n одинаковых конденсаторов:

Конденсаторы соединяют параллельно с целью увеличения емкости батареи и увеличения накапливаемого на ней заряда. Конденсаторы соединяют последовательно для увеличения напряжения на батарее конденсатора.

 

Манипуляции с заряженным конденсатором.

Разведение пластин конденсаторов

Конденсатор отключен от источника:

- заряд остается неизменным

- емкость уменьшается

- напряжение увеличивается

- напряженность электрического поля не изменяется

- энергия увеличивается

Конденсатор подключен к источнику напряжения:

- напряжение не меняется

- емкость уменьшается

- заряд уменьшается

- напряженность электрического поля уменьшается

- энергия уменьшается

Пондеромоторные силы

Пондеромоторные силы это силы притяжения между обкладками конденсаторов.

Выразим эту силу через напряженность электрического поля конденсатора.

,

где 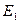- напряженность электрического поля, создаваемого одной пластиной конденсатора.

,

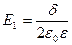где - поверхностная плотность заряда:

(2.10)

Выразим эту силу через напряженность электрического поля конденсатора.

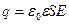. Подставим эту формулу в (2.10)

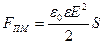(2.11)

Т.к. , то

(2.12)

 

Энергия электростатического поля конденсаторов.

Увеличим расстояние между обкладками заряженного конденсатора на dx (конденсатор отключен от источника). Для этого необходимо приложить силу, минимальное значение которой F_пм.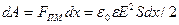

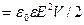(2.13)

- объемная плотность энергии, то есть энергия на единицу объема электростатического поля – объемная доля пространства, занятого электростатическим полем.

(2.14)

 

Постоянный электрический ток.

Электрический ток это направленное движение электрических зарядов. Для осуществления электрического тока необходимо:

1. наличие свободных электрических зарядов

2. наличие электрического поля, энергия которого каким-то образом восполнялась бы и расходовалась бы на упорядоченное движение зарядов.

За направление электрического тока условно, причем направление движения положительных зарядов совпадает с направлением тока. Количественной мерой электрического тока является сила тока I, которая определяется по формуле

(3.1)

Сила тока это заряд, который протекает через сечение проводника в единицу времени. Размерность силы тока – ампер. Электрический ток называется постоянным, если он не меняется со временем.

Для постоянного тока сила тока определяется

(3.1’)

Плотностью тока называется физическая величина, определяемая зарядом, протекающим в единицу времени через единичную площадку, расположенную перпендикулярно направлению движения заряженных частиц. Плотность тока это вектор, за направление которого принято направление внешней нормали к площади поперечного сечения проводника.

(3.2)

(3.3)

Подсчитаем заряд, который протекает через сечение проводника за время dt. Будем считать, что заряд заряженных частиц равен е, концентрация этих частиц равна n, V – средняя скорость упорядоченных частиц. Тогда заряд , сила тока , плотность тока

(3.4).

 

Сторонние силы. ЭДС.

Если на электрические заряды действует только электрическое поле, то будет наблюдаться движение электрических зарядов из точки с большим потенциалом в точку с меньшим потенциалом до тех пор, пока потенциалы не выровняются, следовательно, для постоянного движения зарядов необходимо устройство – так называемый источник тока, в котором создается и постоянно поддерживается постоянная разность потенциалов за счет сил неэлектрического происхождения. Эти силы называются сторонними силами. Сторонние силы совершают работу по перемещению электрических зарядов против сил электрического поля.

Работа по перемещению единичного положительного заряда сторонними силами против сил электрического поля называется электродвижущей силой (ЭДС).

(3.5)

По аналогии с электрической силой мы введем понятие напряженности сторонних сил – это сторонняя сила, действующая на единичный положительный заряд.

(3.6)

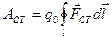
(3.7)

ЭДС, действующая на определенном участке электрической цепи можно определить как

(3.8)

На электрический заряд действуют силы как электрического, так и неэлектрического происхождения. Результирующая сила, действующая на заряд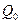

Работа, совершаемая результирующей силой на участке 1-2 равна

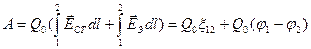
(3.9)

Напряжение – это работа по перемещению единичного положительного заряда под действием как сторонних, так и электрических сил.

(3.10)

Участок электрической цепи, содержащий источник ЭДС, называется неоднородным участком. Формула (3.10) определяют напряжение на концах неоднородного участка цепи.

 

Закон Ома для однородного участка цепи.

Для однородного участка цепи напряжение равно разности потенциалов.

Сила тока на участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению участка.

(3.11)

Сопротивление проводника не зависит ни от напряжения, ни от силы тока, а определяется формой и размерами проводника, а также свойств материала проводника. (3.12),

где l – длина проводника, S – площадь поперечного сечения проводника, - удельное сопротивление проводника.

G – проводимость проводника

– удельная электрическая проводимость .

Сопротивление проводника и его удельное сопротивление практически одинаково зависит от температуры.

(3.13)

где , и значения сопротивления и удельного сопротивления при нуле градусов Цельсия.

(3.14)

При уменьшении температуры для каждого проводника существует некоторая температура, при которой сопротивление проводника резко уменьшается и становится практически равным нулю. Это явление называется явлением сверхпроводимости.

 

Закон Ома в дифференциальной форме.

Подставим выражение для сопротивления в закон Ома и получим:

Учитывая, что 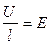и , получим:

(3.15)

Работа и мощность электрического тока. Рассмотрим однородный проводник, к концам которого приложено напряжение U. Для того, чтобы по проводнику прошел электрический ток, нужно переместить заряд между точками с разностью потенциалов U, а для этого совершить работу

(3.16)

(3.16’)

(3/16”)

- закон Джоуля-Ленца.

Мощностью электрического тока называют работу, совершаемую в единицу времени.

(3.17)

(3.18)

 

Закон Джоуля-Ленца в дифференциальной форме

Выделим в проводнике элементарный цилиндрический объем (ось цилиндра совпадает с направлением тока), сопротивление которого . По закону Джоуля-Ленца за время dt в этом объеме выделится теплота . Количество теплоты, выделяющееся за единицу времени в единице объема называется удельной тепловой мощностью тока. Она равна . Используя дифференциальную форму закона Ома и соотношение , получим:

(3.19)

Выражение (3.19) – закон Джоуля-Ленца в дифференциальной форме. Энергия. выделяемая при протекании эл.тока в единицу времени в единицу объема проводника пропорциональна напряженности электрического поля.

 

Закон Ома для неоднородного участка цепи.

Рассмотрим неоднородный участок цепи, где действующую ЭДС на участке 1 — 2 обозначим через 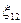, а приложенную на концах участка разность потенциалов — через и .

Если ток проходит по неподвижным проводникам, образующим участок 1- 2, то работа А₁₂ сторонних и электростатических сил, совершаемая над носителями тока, по закону сохранения и превращения энергии равна теплоте, выделяющейся на участке. Работа сил, совершаемая при перемещении заряда 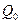на участке 1—2,

За время t в проводнике выделяется теплота

,

откуда

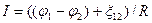(3.20)

Это выражение представляет собой закон Ома для неоднородного участка цепи в интегральной форме, который является обобщенным законом Ома.

 

Частные случаи

1. Если участок цепи однородный, то есть не содержит источника ЭДС, то
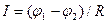
2. Если цепь замкнута, то , то

(3.21)

 

Последовательное и параллельное соединение проводников.

Последовательное соединение называется такое соединение проводников, при котором ток, протекающий через проводник, не изменяется, а напряжение на рассматриваемом участке равно сумме падений напряжений на каждом проводнике.

Формула сложения сопротивлений при последовательном соединении.

(3.22)

(3.23)

Параллельное соединение называется такое соединение проводников, при котором напряжение на всех проводниках одинаково, а ток в цепи равен сумме токов через каждый проводник.

(3.24)

(3.25)

 

Частные случаи:

При соединении двух сопротивлений:

(3.26)

При параллельном соединении n одинаковых сопротивлений:

(3.27)

 

 

Разветвленные цепи постоянного тока.

Любую точку электрической цепи, в которой сходятся три или более проводников, называют узлом.

Первое правило Кирхгофа: Алгебраическая сумма токов в любом узле электрической цепи равна нулю, при этом токи, входящие в узел, принято считать положительными, а выходящие из узла – отрицательными.

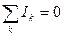(3.28)

Второе правило Кирхгофа: в любом выделенном в электрической цепи замкнутом контуре сумма произведений сил тока на сопротивление равна алгебраической сумме ЭДС, встречающихся в этом контуре:

Порядок применения правил Кирхгофа:

1. Необходимо выбрать (произвольно) направление токов во всех участках разветвленной цепи, отметив на чертежах стрелками.
2. При составлении уравнения соблюдать правило знаков: токи, втекающие в узел, считать положительными, а вытекающие из узла – отрицательными.
3. Иметь в виду, что число уравнений, которые можно составить по первому правилу Кирхгофа всегда на единицу меньше числа узлов в электрической цепи.
4. При написании уравнений по второму правилу Кирхгофа нужно произвольно выбрать направление обхода контура в электрической цепи: по часовой стрелке или против часовой стрелки.
5. При составлении уравнений по второму правилу Кирхгофа, нужно соблюдать правило знаков: токи, совпадающие по направлению с направлением обхода контура, записываются со знаком +, а обратные направлению обхода контура – со знаком “–“.
6. Считать положительными те ЭДС, которые повышают потенциал в направлении обхода (то есть, двигаясь по контуру, сначала встречаешь отрицательный полюс, а потом положительный).
7. Чтобы все уравнения, составленные по второму правилу Кирхгофа, были независимы, необходимо каждый раз выбирать контуры, содержащие хотя бы одну новую ветвь цепи.
8. Для упрощения выкладок, при решении полученной системы уравнений предварительно подставить числовые значения всех известных величин.

 

Электрический ток в различных средах.

Электрический ток в металлах. Носителями тока в металлах являются электроны, которые слабо связаны с ионами кристаллической решетки. Существование свободных электронов в металле можно объяснить следующим образом: при формировании кристаллической решетки металлов в результате действия тока электроны, слабо связанные с атомами, отрываются от атомов металла и могут свободно перемещаться по всему объему. В узлах кристаллической решетки располагаются положительные ионы, а между ними хаотически движутся свободные электроны, образуя так называемый электронный газ, который обладает свойствами обычного идеального газа. Электроны при своем движении сталкиваются с узлами кристаллической решетки, при этом устанавливается термодинамическое равновесие между электронным газом и решеткой. Ис

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: