Главная | Обратная связь | Поможем написать вашу работу!

Для получения электромагнитных колебаний нужно иметь цепь, в которой энергия электрического поля могла бы превращаться в энергию магнитного поля и обратно. Такую цепь называют колебательным контуром.

Занятие №43

Свободные электромагнитные колебании. Превращение энергии в колебательном контуре. Затухающие электромагнитные колебания.

Поскольку магнитное поле получается в соленоиде, а электрическое – в конденсаторе, то простейший колебательный контур состоит из соленоида с индуктивностью L и конденсатора с ёмкостью C. R=0 (Сделать рис).

Активное сопротивление проводников, из которой делают колебательный контур, должно быть достаточно малым, иначе электромагнитные колебания в контуре не возникнут.

Рассмотрим подробнее, как происходят электромагнитные колебания. Зарядим конденсатор емкостью C до некоторого напряжения и соединим его с катушкой, индуктивность которой L На рис. показан момент, когда разрядка конденсатора только начинается. В этот момент в конденсаторе имеется электрическое поле, а магнитного поля в катушке нет, поэтому вся избыточная энергия контура является электрической и выражается формулой = 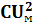/ 2 (Дж).-энергия электрического поля конденсатора.

Когда заряды устремляются из конденсатора в катушку, то в ней создается э.д.с. самоиндукции, которая тормозит нарастание тока, но прекратить его не может. Ток нарастает до тех пор, пока конденсатор не разрядится полностью. В этот момент ток в цепи достигает максимальной величины , а вся избыточная энергия контура является магнитной и выражается формулой = / 2 (Дж).-энергия магнитного поля катушки.

Если активное сопротивление R настолько мало, что потерей энергии на нагревание проводников можно пренебречь, то = 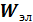. Таким образом, в предельном случаем при R = 0, т.е. при собственных колебаниях в контуре, справедлива формула

/2= / 2.

Собственными называются колебания при отсутствии активного сопротивления в цепи R = 0.

В следующий момент магнитное поле в катушке начинает ослабевать и в ней наводится Э.Д.С. самоиндукции, поддерживающая прежнее направление тока, вследствие чего происходит перезарядка конденсатора, т.е. превращение магнитной энергии в электрическую.

Когда магнитное поле в катушке исчезнет, то конденсатор опять начинает разряжаться и в контуре возникает ток обратного направления, пока вся электрическая энергия снова не перейдет в магнитную. Итак, полное колебание в контуре закончено, и далее весь описанный процесс повторяется снова в том же порядке.

Время, затраченное на одно полное колебание, есть период электромагнитных колебаний T, а их число в единицу времени – частота колебаний =1/ T.

Как показывает теория, колебания в идеальном контуре (при R = 0), т.е. собственные колебания, являются гармоническими. Период собственных колебаний определяется условием равенства реактивных сопротивлений катушки и конденсатора, т.е. формулой

= , или L= 1 / C

Частоту , при которой выполняется это равенство, называют собственной частотой колебательного контура.

= 1/ .

Поскольку = 2∏/ T, то для периода собственных колебаний в контуре получим

T = 2∏ .

Это соотношение называют формулой Томпсона

Из предыдущей формулы следует, что для частоты v собственных колебаний в контуре получим

Из формулы = видно, что при достаточно малых L и C в контуре можно получить колебания высокой частоты, измеряемой миллионами герц и выше.

Затухающие электромагнитные колебания. Электрический резонанс.

Колебательный контур имеет некоторое активное сопротивление R, то, когда заряженный конденсатор, обладающий энергией W, соединяют с катушкой, при каждом колебании происходит уменьшение избыточной энергии контура W, так как она расходуется на нагревание проводников контура. Это означает, что в реальных случаях свободные колебания в контуре являются затухающими т.к R не= 0. Очевидно, что скорость затухания колебаний будет возрастать при увеличении активного сопротивления контура R, которое действует аналогично трению в механических колебаниях.

Чтобы получить незатухающие электромагнитные колебания, можно включить в колебательный контур источник внешней синусоидальной Э.Д.С. Под действием этой Э.Д.С. в контуре установятся вынужденные колебания с частотой этого источника (т.е. потечет переменный ток).

Если теперь изменять частоту внешнего источника , то амплитуда вынужденных электромагнитных колебаний будет изменятся, как и в случае механических колебаний.

Когда частота внешнего источника приближается к собственной частоте контура, наступает электрический резонанс. При совпадении этих частот = (реактивные сопротивления конденсатора 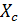и катушки взаимно компенсируют друг друга) ток в колебательном контуре резко возрастает, так как его значение при этом, ограничивается только активным сопротивлением контура R, которое обычно мало. Соответственно возрастают падения напряжения катушки 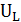= I . При резонансе амплитуды этих напряжений могут в десятки и сотни раз превышать амплитуду э.д.с.. Заметим, что собственную частоту контура, определяемую выражением = 1/ , называют резонансной частотой контура.

При увеличении активного сопротивления контура R резонансные кривые идут ниже. При электрическом резонансе цепь фактически обладает только активным сопротивлением, т.е. нет сдвига фаз между силой тока и напряжением, хотя до и после резонанса этот сдвиг фаз есть.

Проанализируем формулу:

при R —> 0 (I_max)_рез. —> 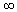(чем меньше активное сопротивление R, тем более острый максимум имеет резонансная кривая);
при R —> 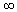говорить о резонансе не имеет смысла.

Таким образом: резонанс в электрической цепи переменного тока – явление резкого возрастания амплитуды вынужденных колебаний силы тока в колебательном контуре при совпадении частоты внешнего переменного напряжения с частотой свободных незатухающих колебаний в контуре.

Явление электрического резонанса широко используется при осуществлении радиосвязи в схемах настройки радиоприёмников (для выделения сигнала требуемой частоты), усилителей, генераторов высокочастотных колебаний. На явлении резонанса основана работа многих измерительных приборов. Например, резонансный волномер используется для измерения частоты и является основной частью генераторов стандартных сигналов.

Воспользуйтесь поиском по сайту: