 |
Формализация процесса функционирования системы
|
|
|
|
Задание на выполнение курсовой работы представлено, как правило, в виде функциональной схемы системы автоматизации, либо в виде содержательного описания технологического процесса (объекта управления). Процесс формализации может быть сведен к следующим пунктам:
- изучить объект и процессы, происходящие в нем, выделить входные и выходные переменные, уточнить зависимые и независимые переменные, значения параметров в нормальном режиме и т.п.;
- установить перечень технологических параметров, определяющих данный процесс или систему управления;
- определить цель и показатели качества функционирования объекта управления;
- определить совокупность всех исходных данных;
- принять необходимые допущения и упрощения;
- провести декомпозицию объекта управления или системы управления;
- составить содержательное описание моделируемого процесса (объекта или системы управления);
- провести вычислительный эксперимент.
Таким образом, процесс формализации является промежуточным звеном между содержательным описанием и построением математической модели системы управления. Содержательное описание включает необходимые сведения, достаточные для построения формализованного описания системы, но не дает ответа о точных соотношениях между параметрами технологического процесса (объекта управления).
3. Построение математической модели
Математической моделью технологического процесса (объекта управления) называют систему математических отношений между входными и выходными параметрами процесса и конструктивными величинами, показателями качества, а также ограничения, накладываемые на параметры.
Для перехода от содержательного описания к математической модели необходимо:
|
|
|
- провести декомпозицию объекта, разделив его на элементарные блоки, узлы, контуры, процессы, элементы и составить структурную схему объекта;
- для каждого блока, элемента, контура составить уравнения, описывающие его поведение и определить математические соотношения между параметрами и показателями процесса;
- определить ограничения на параметры;
- записать все математические соотношения между элементами системы управления;
- выразить все логические условия работы в виде системы неравенств;
- получить аналитические выражения для передаточных функций по кривым разгона или другим данным;
- при необходимости линеаризовать нелинейные соотношения, в этом случае необходимо помнить, что линеаризованные зависимости отражают достаточно точно процесс лишь в точке разложения.
Для математического описания процессов, происходящих в объекте необходимо использовать:
- уравнения материального, теплового и энергетического баланса с учетом гидродинамики потоков и физических свойств жидкостей;
- уравнения элементарных процессов (массо- и теплообмена, химических реакций, переходных процессов в электрических цепях);
- теоретические и эмпирические соотношения между параметрами процесса (уравнения идеальных газов, изотермических процессов, зависимости массопередачи от скорости потока фаз, законы Кирхгофа, Ома, и т.д.);
- ограничения на параметры процесса.
При построении математической модели используются:
- алгебраические уравнения для описания статических, стационарных, режимов работы;
- обыкновенные дифференциальные уравнения для описания динамических объектов с сосредоточенными параметрами или с распределенными параметрами;
- дифференциальные уравнения в частных производных могут быть использованы для описания статических моделей объектов с распределенными параметрами по нескольким координатам или для описания динамических нестационарных процессов объектов с распределенными параметрами;
|
|
|
- для описания объектов со случайной природой используются вероятностные модели и статистические характеристики входных и выходных параметров объектов.
Для упрощения описания должны быть приняты ряд допущений, упрощающих описание моделируемого объекта (например, допущения о cтационарности процесса, об изотермическом процессе расширенного газа, об отсутствии активного сопротивления индуктивности и емкости и др.)
При необходимости проводится линеаризация полученных нелинейных выражений в точке нормального технологического процесса разложением в ряд Тейлора.
Например, для функции двух переменных а1, а2:

 (1)
(1)
где f(a1,a2) - заданная функция со значением f (a10,a20) в точке разложения;
 - частные производные, вычисленные в точке разложения;
- частные производные, вычисленные в точке разложения;
Е - остаточные члены ряда с порядком и производными выше первой (отбрасываются).
В результате проведенной работы должно быть получено математическое описание моделируемого объекта в виде уравнений, содержащих входные и выходные координаты объекта, а также начальные и граничные условия и ограничения
4. Принципы и правила построения математической модели
При построении модели нужно придерживаться ряда принципов и правил моделирования.
Принципы определяют общие свойства, которыми должна обладать модель. Правила дают способы получения нужных свойств.
Принцип 1. При построении математических моделей нужно достигать компромисса между ожидаемой точностью результатов моделирования и сложностью упрощений (Выбрать путь между болотом усложнений и пропастью упрощений). Критерием компромисса могут служить время реализации модели, требуемые ресурсы и т.д.
Принцип 2 Создаваемая математическая модель должна удовлетворять требованию баланса точностей:
- систематическая погрешность моделирования (отклонение модели от описания) и погрешность в задании параметров описания (исходная неопределенность) должны быть одного порядка;
- математические модели составляющих элементов должны быть одного порядка точности;
- систематическая погрешность моделирования и случайная погрешность при интерпретации и усреднении результатов моделирования должны быть одного порядка.
|
|
|
Правило 1. При разработке математических моделей сложных систем следует проводить параллельное моделирование конкурирующих вариантов исследуемой системы с оценкой разности или отношения соответствующих показателей.
Чтобы можно было реализовать принципы 1 и 2 необходимо иметь достаточное количество вариантов.
Принцип 3 Для реализации математических моделей исследуемой системы необходимо иметь достаточное разнообразие вариантов.
Принцип 4 Создаваемая модель должна быть наглядной для исследователя и потребителя.
Принцип 5 Модели сложной системы должны иметь модульную структуру.
Переход от формализованного описания системы к ее модели целесообразно проводить путем исключения отдельных элементов описания и создания модулей. Разделение на модули зависит от проведенного ранее анализа, имеющегося программного обеспечения и опыта исследователя, но с соблюдением принципа информационной связи.
Правило 2 Обмен информацией между блоками должен быть минимальным.
При упрощении структурной схемы следует пользоваться следующими правилами.
Правило 3 Удалять без замены следует такие элементы модели, которые мало влияют на принятый критерий качества моделирования.
Правило 4 Замена или удаление модулей, с помощью которых моделируемая система взаимодействует с "пользователем", должна производится с учетом интересов "пользователя".
При моделировании нескольких возмущений на исследуемый объект бывает невозможно определить характеристики возмущений при автономном исследовании одного блока возмущения. Поэтому характеристики возмущения определяют путем многократных испытаний системы по всему диапазону изменения для каждого вида возмущения.
Следует также выбрать вид возмущений: детерминированный или случайный, сопоставляя результаты моделирования.
Правило 5 Блоки модели, осуществляющие воздействие на исследуемую систему в общем случае можно заменить на:
|
|
|
- блок с наихудшим воздействием на систему:
- множество упрощенных блоков, каждый из которых моделирует одно возмущение в одном диапазоне, а моделирование проводить в нескольких вариантах.
Декомпозицию системы и объекта управления можно проводить либо по структурным единицам системы, либо по режимам эксплуатации. Последний способ разделения позволяет упростить схему моделирования и уменьшить разброс результатов моделирования и, следовательно, сократить время исследования.
Принцип 6 При анализе сложной системы управления в заданном режиме допускается использование набора малых частных моделей, что позволяет судить о свойствах системы в целом по результатам, полученным на частных моделях.
Специализация (сужение класса решаемых задач) полной модели позволяет проверить точность упрощенного ее представления в отдельных ситуациях.
Правило 6 Для проверки соответствия частной модели wi полной модели W следует построить условные модели wi+1, эквивалентные wi в типовых ситуациях.
Правило 7 Проверку соответствия wi и полной модели W следует вести по сходимости результатов, получаемых на моделях возрастающей сложности.
В соответствии с принципом 2 различие, определяемое по результатам эксперимента с двумя последовательными моделями, можно считать несущественным, если это различие находится в пределах допуска определяемое погрешностями исходных данных.
Правило 8 Расчет допусков проводится по наиболее простой модели, включающей все неточные параметры описания. Как правило, в качестве такой модели принимают аналитическую модель, позволяющую получить качественную оценку системы.
5. Составление моделирующего алгоритма
Чтобы моделировать любой процесс, систему управления или объект управления, заданного в виде математической модели необходимо построить моделирующий алгоритм. Для решения этой задачи можно использовать математическую модель:
- заданную в виде системы уравнений относительно искомых величин;
- заданную в виде математических соотношений, с сохранением логической структуры, последовательности чередования во времени характера и состава информации о состояниях и физическом содержании процесса;
- заданную в виде структурной схемы, составленной из типовых элементов, заданных передаточными функциями с известными коэффициентами полиномов.
Для математической модели, заданной в виде системы алгебраических или дифференциальных уравнений, алгоритм реализуется одним из известных численных методов. Результаты моделирования представляют собой решение заданной системы уравнений.
|
|
|
Если для решения задачи моделирования необходимо использовать численные методы, не реализованные в виде готовых программ, то на этапе алгоритмизации и программирования решаются задачи: выбора численного метода решения, составления алгоритма, написания и отладки программы и получения решения.
При выборе численного метода предпочтение следует отдавать методам, дающим решение за конечное число машинных операций. Недостатком любого метода является накопление ошибок машинных вычислений, производимых с конечным числом значащих цифр. Поэтому целесообразно использовать численные методы с автоматическим выбором шага. Допускается использование готовых программ, процедур реализующих выбранный численный метод.
При составлении алгоритма решения задачи нужно использовать графические символы (ГОСТ 19.003-80). Основными требованиями к содержанию записи алгоритмов являются наглядность, компактность и выразительность.
После составления и проверки алгоритма пишется программа на одном из языков программирования. Программа проверяется и отлаживается на контрольном примере.
Во втором случае в соответствии с моделирующим алгоритмом в ЭВМ вырабатывается информация, имитирующая элементарные явления, составляющих моделируемый процесс с сохранением их логической структуры. Явления исследуемого процесса и явления, происходящие в ЭВМ, реализующей алгоритм, должны быть близкими с точки зрения состава и характера информации, описывающей проведение реальной системы, и информации, перерабатываемой ЭВМ.
В третьем случае модель реализуется в виде соединения типовых блоков используемого пакета программ моделирования или аналогово-цифровых комплексов.
Разработка моделирующего алгоритма должна быть доведена до уровня структурных схем в виде соединения типовых блоков. Описание моделирующего алгоритма должно содержать:
- общую структурную схему моделирования и ее описание;
- форматы вводимой и выводимой информации;
- перечень стандартных подпрограмм, используемых при моделировании.
Структурная схема моделирования может быть двух видов:
- в первом виде отражается логика работы всей модели, с отражением связей ее модулей между собой;
- во втором виде отражена детальная работа каждого крупного элемента (блока) основного алгоритма, логическая последовательность вычислений, получаемой и выводимой информации в каждом блоке основного алгоритма.
8. Задание на курсовую работу
1. Составить математическую модель распространения тепловых полей в заданном объекте. При этом размеры объекта вычисляются по формулам (1), (№ варианта N соответствует номеру по списку).
2. Составить дискретную модель рассматриваемого объекта.
3. Разработать алгоритм и составить программу в виде модуля, вычисления температурных полей на ЦВМ, описывающего объект.
4. Для указанной преподавателем точки построить график переходного процесса.
Четные номера (пластина)

 |
Не четные номера вариантов (цилиндрический стержень)
Рис. 1. Варианты заданий.
| N | S1 | S2 | S3 | S4 | S5 | S6 |
| T | ||||||
| q | ||||||
| T | ||||||
| T | ||||||
| T | ||||||
| T | ||||||
| T | ||||||
| q | ||||||
| q | ||||||
| q | ||||||
| q | ||||||
| q | ||||||
| q | ||||||
| T | ||||||
| q |
 ,
,  ,
, 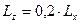 ,
,  ,
,
где Т – входное воздействие в виде заданной температуры; q – входное воздействие – тепловой поток; 1 – температура поверхности равна 0;
0 – поверхность теплоизолирована.
Нечетные номера (цилиндр)
| N | S1 | S2 | S3 |
| T | |||
| q | |||
| T | |||
| q | |||
| T | |||
| q | |||
| T | |||
| q | |||
| T | |||
| T | |||
| q | |||
| T | |||
| q | |||
| T | |||
| q |
Рекомендуемая литература
1. Рей У. Методы управления технологическими процессами. - М.: Мир, 1983. - 367 с.
2. Ротенберг Я.Н. Автоматическое управление. - М.: Наука, 1971.- 395 с.
3. Архангельский А.Я. Приемы программирования в Delpi м. Бином 2004.-847с.
4. Лыков А.В. Теория теплопроводности – М.: Высшая школа, 1967 – 599 с.
5. Демидович Б.П., Марон. И.А. Основы вычислительной математики. —М.: Наука, 1956. — 664 с.
6. Галисеев Г.В. Программирование в среде Delpi-7.-М.:Диалектика, 2003-286с.
Приложение 1.
Титульный лист курсовой работы.
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГОПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Пятигорский Государственный Технологический Университет
Кафедра УИТС
КУРСОВАЯ РАБОТА
По дисциплине «Объектное программирование»
Тема _____________________
_________________________
__________________________
__________________________
Исполнитель: студент ____ курса ____группы ______факультета
Фамилия, имя, отчество__________________________________
Руководитель __________________________________________
Курсовая работа допущена к защите
«____»__________________200_ г.
Защитил курсовую работу с оценкой
_______________________________
«____»__________________200_ г.
Пятигорск, 200_ г.
|
|
|


