Основные теоремы о пределах

Непрерывность функции

Функция называется непрерывной в точке , если:

1. эта точка принадлежит области определении функции;

2. приращение функции в этой точке стремится к нулю, когда стремится к нулю приращение аргумента .

Функция

называется непрерывной на некотором множестве , если она непрерывна в каждой точке этого множества.

Точка, в которой нарушается непрерывность функции, называется точкой разрыва. Разрыв функции в точке может произойти в результате невыполнения одного из двух условий:

1. функция определена в точке , но при приращении аргумента , стремящемся к нулю, приращение функции не стремится к нулю;

2. функция не определена при и говорить о приращении функции не имеет смысла. В этом случае может быть точкой разрыва, если она является граничной точкой определения функции.

 

Предел функции

Пусть функция определена и непрерывна в некоторой окрестности точки , за исключением, может быть, самой точки . При этих условиях в точке функция либо непрерывна, либо терпит разрыв. В последнем случае бывает возможно доопределить функцию или переопределить её по непрерывности в точке , т. е. приписать в точке такое значение , при котором функция окажется непрерывной в этой точке.

Пример 1. Функция

изображённая на рис. 6, определена на всей числовой прямой, но терпит разрыв – скачок при x = 1. Однако в точке x = 1 функцию можно переопределить, заменив значение 3 на 1. Тогда получим функцию

или, короче,

непрерывную на всей числовой прямой.

Пример 2. Функция

изображённая на рис. 8, не определена при значении x = -1, которое обращает знаменатель в нуль, т.е.

Эта функция не равна функции

получаемой в результате сокращения правой части f (x) на x + 1, так как функции f (x) g (x) имеют разные области определния. График функции f (x) отличается от графика g (x) отсутствием лишь одной точки и имеет разрыв при x = -1. Но f (x) можно доопределить в точке x = -1 так, что функция станет непрерывной в этой точке, для чего значение функции в указанной точке следует считать равным -2. Тогда получим функцию

непрерывную на всей числовой прямой и равную функции g (x) = -1.

Если - точка разрыва функции f (x), но возможно доопределить по непрерывности f (x) в этой точке, т.е. выбрать для неё в точке такое значение a, при котором изменённая или дополненная функция

станет непрерывной, то число a называют пределом функции f (x) в точке , а точку - точкой устранимого разрыва.

Это записывается так:

Разумеется, если функция f (x) определена и непрерывна в точке , то нет надобности в доопределении её по непрерывности в этой точке. В этом случае

(1)

Замечание 1. Так как все элементарные функции непрерывны в области определения, то в каждой точке области определения для них справедливо равенство (1).

 

Результаты, полученные в примерах 1 и 2, теперь можно записать короче:

Основные теоремы о пределах

Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела.

Следствие. Если две функции f (x) и g (x) равны в некоторой окрестности точки , за исключением, может быть, самой точки , то либо они имеют один и тот же предел при 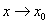, либо обе не имеют предела в этой точке.

Теорема 2. Если функции f(x) и g(x) имеют пределы в точке , то:

1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.

(2)

2) предел произведения функций равен произведению пределов сомножителей, т.е.

(3)

3) предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.

(4)

Замечание. Формулы (2) и (3) справедливы для любого конечного числа функций.

Следствие 1. Предел постоянной равен самой постоянной, т.е.

Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.

Пример 6. Найти

Решение.

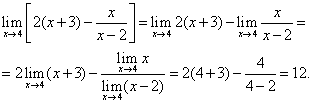
Пример 7. Найти

Решение. Предварительно убедимся, что предел делителя не равен нулю:

Таким образом, формула (4) применима и, значит,

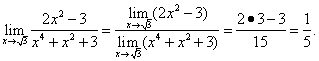
Теорема 3 (о пределе сложной функции). Если существует конечный предел

а функция f(u) непрерывна в точке , то

Другими словами, для непрерывных функций символы предела и функции можно поменять местами.

Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.

Пример 8. Найти

Решение. Теорема о пределе частного здесь неприменима, так как

Преобразуем заданную дробь, разложив числитель и знаменатель на множители. В числителе получим

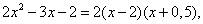
где

корни квадратного трёхчлена. Теперь, полагая , сократим дробь и, используя следствие из теоремы 1, вычислим предел данной функции:

Предел последовательности

Бесконечной числовой последовательностью называется числовая функция

определённая на множестве натуральных чисел.

Число a называется пределом последовательности 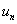, если для произвольно малого положительного числа 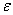найдётся такое число N, что для всех членов последовательности, номер которых , выполняется неравенство

Это записывается так:

Символ 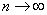означает, что n неограниченно возрастает. Если последовательность имеет предел, то её называют сходящейся, в противном случае – расходящейся.

Замечание. Для сходящихся последовательностей справедливы все ранее рассмотренные свойства пределов.

Пример 9. Найти предел

Решение.

Числитель дроби – величина постоянная, а знаменатель неограниченно возрастает, поэтому дробь, оставаясь положительной, убывает, стремясь к нулю.

Поделиться:

Воспользуйтесь поиском по сайту: