 |
Дискретизация аналоговых сигналов во времени. Дискретизация одномерного сигнала. Теорема Котельникова для одномерного сигнала.
|
|
|
|
Спектры цифровых сигналов, применение дискретного преобразования Фурье.
Рассмотрим периодический сигнал, удовлетворяющий условиям:

Указанный сигнал может быть представлен в виде симметричного спектра положительных и отрицательных частот:
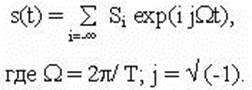
Амплитуда i-й гармоники такого сигнала имеет вид:

Симметричный амплитудный спектр такого сигнала может быть выражен в виде:
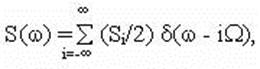
Произвольный сигнал s(t) также может быть разложен на гармонические составляющие. Указанное разложение получается, если период Т сигнала стремится к бесконечности, а частота, соответственно к нулю. В этом случае ряд Фурье преобразуется в интеграл Фурье:

Обратное преобразование Фурье формирует из спектра исходную функцию:

Выравнивающий коэффициент (2p)-1 относят к прямому преобразованию Фурье, обратному преобразованию, или используют коэффициент (2p)-1/2.
Спектр пространственного сигнала.
Для существования спектра необходимо, чтобы функция s(t) удовлетворяла условиям Дирихле. Одним из наиболее жестких условий, вытекающих из ограничений Дирихле, является абсолютная интегрируемость функции s(t).

В общем случае сигнал монохромного (одноцветного) подвижного изображения является трехмерной функцией двух пространственных координат x и y и времени t: s(x, y, t). Спектр такого сигнала выражается в виде

Обратное восстановление трехмерного сигнала производится по зависимости:

Условие абсолютной интегрируемости трехмерной функции имеют вид:

Трехмерная -функция Дирака определяется в виде


Можно доказать, что спектр последовательности трехмерных -функций c периодами в измерениях t, x, y, равными Т, X, Y соответственно, и бесконечных в каждом измерении, представляет собой бесконечную периодическую последовательность -функций с периодами  соответственно,
соответственно,
|
|
|

причем между периодами следования -функций в сигнальной области и периодами следования -функций в спектральной области существуют соотношения:

Дискретизация аналоговых сигналов во времени. Дискретизация одномерного сигнала. Теорема Котельникова для одномерного сигнала.
Преобразование аналогового сигнала в цифровой состоит из двух этапов: дискретизации по времени и квантования по амплитуде. Дискретизация по времени означает, что сигнал представляется рядом своих отсчетов (семплов), взятых через равные промежутки времени. Например если частота дискретизации 44,1 кГц, то это значит, что сигнал измеряется 44100 раз в течении секунды (обычно применяется более доходчивый термин "частота семплирования", однако "частота дискретизации" правильнее.
Чем больше частота - тем точнее соответствует цифровой сигнал аналоговому. Однако, пропорционально увеличению частоты возрастают: а) интенсивность потока цифровых данных, а пропускные возможности интерфейсов не безграничны, особенно если записывается/воспроизводится одновременно несколько каналов; б) вычислительная нагрузка на цифровые процессоры эффектов, а их вычислительные возможности также ограничены; в) объем памяти, необходимой для хранения цифрового сигнала
Дискретизация - преобразование непрерывной функции в дискретную.
При дискретизации во времени непрерывный аналоговый сигнал заменяется последовательностью отсчётов, величина которых может быть равна значению сигнала в данный момент времени. Возможность точного воспроизведения такого представления зависит от интервала между отсчётами ∆t.
Исключительно важным положением теории связи, на котором основана вся современная радиотехника, является так называемая теорема отсчетов, или теорема Котельникова. Эта теорема позволяет установить соотношение между непрерывными сигналами, какими являются большинство реальных информационных сигналов – речь, музыка, электрические сигналы, соответствующие телевизионным изображениям, сигналы в цепях различных радиотехнических систем и т.п., и значениями этих сигналов лишь в отдельные моменты времени – так называемыми отсчетами.
|
|
|
Согласно теореме Котельникова ∆t< 1/(2*Fmax), где Fmax - наибольшая частота спектра сигнала.
Теорема Котельникова: частота спектра должна быть в 2 раза меньше частоты дискретизации
|
|
|


