 |
Дифференциальные уравнения первого порядка
|
|
|
|
Полный дифференциал функции нескольких переменных
Частной производной по  от функции
от функции  называется предел отношения частного приращения этой функции
называется предел отношения частного приращения этой функции  по
по  к приращению
к приращению 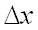 , когда последнее стремится к нулю:
, когда последнее стремится к нулю:

Частной производной по  от функции
от функции  называется предел отношения частного приращения этой функции
называется предел отношения частного приращения этой функции  по
по  к приращению
к приращению  , когда последнее стремится к нулю:
, когда последнее стремится к нулю:
 .
.
Пусть задана функция  . Если аргументу
. Если аргументу  сообщить приращение
сообщить приращение 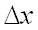 , а аргументу
, а аргументу  – приращение
– приращение  , то функция
, то функция  получит приращение
получит приращение  , которое называется полным приращением функции и определяется формулой:
, которое называется полным приращением функции и определяется формулой:  .
.
Функция  , полное приращение
, полное приращение  которой в данной точке может быть представлено в виде суммы двух слагаемых (выражения, линейного относительно
которой в данной точке может быть представлено в виде суммы двух слагаемых (выражения, линейного относительно 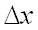 и
и  , и величины бесконечно малой высшего порядка относительно
, и величины бесконечно малой высшего порядка относительно  ):
):
 ,
,
где  и
и  стремятся к нулю, когда
стремятся к нулю, когда 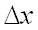 и
и  стремятся к нулю (т.е. когда
стремятся к нулю (т.е. когда  ), называется дифференцируемой в данной точке.
), называется дифференцируемой в данной точке.
Линейная (относительно 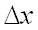 и
и  ) часть полного приращения функции называется полным дифференциалом и обозначается
) часть полного приращения функции называется полным дифференциалом и обозначается  :
:
 ,
,
где  и
и  – дифференциалы независимых переменных, которые, по определению, равны соответствующим приращениям
– дифференциалы независимых переменных, которые, по определению, равны соответствующим приращениям 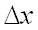 и
и  .
.
Частные производные от частных производных первого порядка называются частными производными второго порядка. Для функции двух переменных  их четыре:
их четыре:
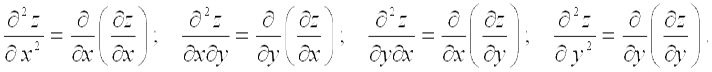
Дифференциальные уравнения первого порядка
Дифференциальным уравнением первого порядка называют соотношение вида  , где
, где  – независимая переменная (аргумент),
– независимая переменная (аргумент),  – неизвестная функция аргумента
– неизвестная функция аргумента  – заданная функция трех переменных
– заданная функция трех переменных  , изменяющихся в некоторой области трехмерного пространства.
, изменяющихся в некоторой области трехмерного пространства.
1) Дифференциальные уравнения с разделяющимися переменными
Дифференциальным уравнением с разделяющимися переменными в высшей математике называется дифференциальное уравнение первого порядка вида 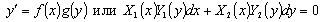
|
|
|
Пример
Решить уравнение  . В частности, найти решение, удовлетворяющее начальному условию
. В частности, найти решение, удовлетворяющее начальному условию 
Учитывая, что 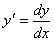 и вынося за скобки y, получим
и вынося за скобки y, получим  , или, что то же самое,
, или, что то же самое,  . Разделив обе части уравнения на произведение
. Разделив обе части уравнения на произведение  получим:
получим:  . Интегрируем обе части последнего равенства:
. Интегрируем обе части последнего равенства:  . Учитываем то, что
. Учитываем то, что  и сокращаем обе части равенства на
и сокращаем обе части равенства на  :
:  . Произвольную постоянную
. Произвольную постоянную  удобно представить в виде
удобно представить в виде  . Тогда
. Тогда  , откуда и получаем ответ
, откуда и получаем ответ 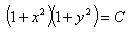 . Учтем заданное условие
. Учтем заданное условие  . Следовательно, искомое частное решение есть
. Следовательно, искомое частное решение есть  .
.
2) Однородные дифференциальные уравнения
Дифференциальное уравнение  называется однородным, если
называется однородным, если  – однородная функция нулевой степени.
– однородная функция нулевой степени.
Дифференциальное уравнение первого порядка в симметричной форме  является однородным, если
является однородным, если  – однородные функции одной степени.
– однородные функции одной степени.
Замена  приводит однородное уравнение к уравнению с разделяющимися переменными.
приводит однородное уравнение к уравнению с разделяющимися переменными.
Пример
Решить уравнение  . Найти решение, удовлетворяющее начальному условию
. Найти решение, удовлетворяющее начальному условию  .
.
Данное уравнение однородное. Произведя замену  , получим
, получим  (здесь мы учли, что
(здесь мы учли, что 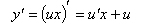 ). Сокращаем на
). Сокращаем на 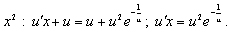 . Учитывая, что
. Учитывая, что 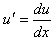 , получим
, получим  . Интегрируем полученное равенство:
. Интегрируем полученное равенство:  . Обозначая
. Обозначая  и учитывая
и учитывая  , получаем ответ
, получаем ответ  . Для данного начального условия
. Для данного начального условия 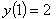 :
:  . Следовательно, искомое частное решение есть
. Следовательно, искомое частное решение есть  .
.
3) Линейные дифференциальные уравнения первого порядка
Дифференциальные уравнения вида  называются линейными. Существуют несколько методов их решения: метод Бернулли, метод Лагранжа, метод интегрирующего множителя.
называются линейными. Существуют несколько методов их решения: метод Бернулли, метод Лагранжа, метод интегрирующего множителя.
Метод Бернулли
Решение уравнения  ищется в виде
ищется в виде  . При этой замене получаем:
. При этой замене получаем: 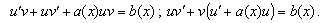 Функцию
Функцию  выбирают из условия
выбирают из условия  . Полученную функцию
. Полученную функцию  подставляют в уравнение
подставляют в уравнение  (учитываем
(учитываем  ), решая которое находят функцию
), решая которое находят функцию  .
.
Пример
Решить уравнение 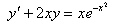 .
.
Полагая  и учитывая
и учитывая  , получим
, получим  . Преобразуем полученное уравнение:
. Преобразуем полученное уравнение:  . Функцию
. Функцию  выберем из условия u`+ 2xu = 0. Учитывая
выберем из условия u`+ 2xu = 0. Учитывая  , получаем
, получаем  . Интегрируем это равенство:
. Интегрируем это равенство:  (см. примечание).
(см. примечание).
Подставляя полученный результат  в уравнение
в уравнение  , и учитывая, что при
, и учитывая, что при  , получим
, получим  . Сократим последнее равенство на и учтем
. Сократим последнее равенство на и учтем  . Учитывая
. Учитывая  , ответ будет таким:
, ответ будет таким:  .
.
Примечание
При интегрировании равенства  , получается результат
, получается результат  , откуда следует, что
, откуда следует, что  или
или  . Однако в методе Бернулли нас интересует не все множество функций
. Однако в методе Бернулли нас интересует не все множество функций  , а лишь одна функция из этого множества. Проще всего принять
, а лишь одна функция из этого множества. Проще всего принять 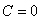 и выбрать
и выбрать  , тогда
, тогда  .
.
|
|
|
Кратные интегралы
 формула вычисления двойного интеграла по области
формула вычисления двойного интеграла по области 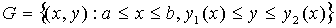 с помощью повторного интегрирования.
с помощью повторного интегрирования.
 - формула замены переменных в двойном интеграле; здесь
- формула замены переменных в двойном интеграле; здесь  - функции задающие отображение области g на область G.
- функции задающие отображение области g на область G.
 - площадь области G на плоскость Oxy.
- площадь области G на плоскость Oxy.
 - площадь области g на плоскости G через криволинейные координаты u, v; здесь g – прообраз области G при отображении
- площадь области g на плоскости G через криволинейные координаты u, v; здесь g – прообраз области G при отображении 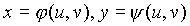
 - элемент площади в криволинейных координатах u, v.
- элемент площади в криволинейных координатах u, v.
 ,
, 
 - формулы перехода к полярным координатам
- формулы перехода к полярным координатам  ;
;
 - якобиан перехода.
- якобиан перехода.
 - объем тела
- объем тела 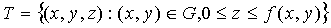
 -формула вычисления тройного интеграла по области
-формула вычисления тройного интеграла по области  с помощью повторного интегрирования.
с помощью повторного интегрирования.
 - формула вычисления тройного интеграла по области
- формула вычисления тройного интеграла по области  с помощью повторного интегрирования.
с помощью повторного интегрирования.
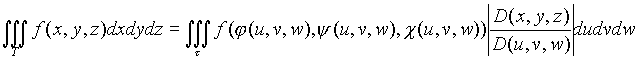 -формула замены переменных в тройном интеграле, здесь
-формула замены переменных в тройном интеграле, здесь  -функции задающие отображение области
-функции задающие отображение области  на Т.
на Т.
 - объем тела Т в пространстве Оху.
- объем тела Т в пространстве Оху.
 - выражение объема тела в пространстве Oxyz через криволинейные координаты u, v, w; здесь
- выражение объема тела в пространстве Oxyz через криволинейные координаты u, v, w; здесь  - прообраз тела Т при отображении
- прообраз тела Т при отображении  .
.
 -элемент объема в криволинейных координатах u, v, w.
-элемент объема в криволинейных координатах u, v, w.
 -формулы перехода к цилиндрическим координатам
-формулы перехода к цилиндрическим координатам 
 - якобиан перехода.
- якобиан перехода.
 ,
,  ,
, 
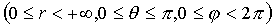 - формулы перехода к сферическим координатам
- формулы перехода к сферическим координатам  ;
;  - якобиан перехода.
- якобиан перехода.


 ,
,  - формулы перехода к обобщенным сферическим координатам;
- формулы перехода к обобщенным сферическим координатам;  - якобиан перехода.
- якобиан перехода.
|
|
|


