 |
Перечислите логические элементы компьютера. Охарактеризуйте и укажите их обозначения. Изобразите схему с использованием логических элементов.
|
|
|
|
Алгебра логики
5. Дайте определение понятий: алгебра логики и высказывание. Укажите виды высказываний и охарактеризуйте их. Приведите примеры таких высказываний.
Дайте определение операций алгебры логики: инверсия, конъюнкция, дизъюнкция, импликация, эквиваленция. Укажите порядок их выполнения. Составьте для них таблицы истинности.
Дайте определение понятию логическая формула. Приведите пример. Укажите порядок выполнения логической операций в формулах. Покажите на примере построение таблицы истинности для логической формулы.
Перечислите логические элементы компьютера. Охарактеризуйте и укажите их обозначения. Изобразите схему с использованием логических элементов.
Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Логическое высказывание — это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo.
Например, предложение "6 — четное число" следует считать высказыванием, так как оно истинное. Предложение "Рим — столица Франции" тоже высказывание, так как оно ложное.
Виды высказываний:
1) Элементарные (простые) логические высказывания и
2) составные логические высказывания.
Элементарное логическое высказывание — это повествовательное предложение, о котором имеет смысл говорить, истинно оно или ложно. (Иванов — футболист)
Составное логическое высказывание- набор простых высказываний, связанных логическими операциями.
Логическая связка — это любая логическая операция над высказыванием. Например, употребляемые в обычной речи слова и словосочетания «не», «и», «или», «если…, то», «тогда и только тогда» являются логическими связками.
|
|
|
«Иванов — футболист и шахматист» — составное логическое высказывание, состоящие из двух элементарных высказываний, связанных между собой при помощи связки «и».
Основные операции над логическими высказываниями (логические связки)
- КОНЪЮНКЦИЯ
- ДИЗЪЮНКЦИЯ
- ИНВЕРСИЯ
- Импликация
- ЭКВИВАЛЕНТНОСТЬ
- Строгая дизъюнкция.
1) Конъюнкция (логическое умножение) двух логических высказываний (И,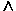 
или &) — логическое высказывание, истинное только тогда, когда они одновременно истинны.
Таблица истинности
Примеры:
10 делится на 2 (A - и). 5 больше 3 (B - и). 10 делится на 2 и 5 больше 3 (A & B - и).
10 не делится на 2 (A - л). 5 больше 3 (B - и). 10 не делится на 2 и 5 больше 3 (A & B - л).
10 делится на 2 (A - и). 5 не больше 3 (B - л). 10 делится на 2 и 5 не больше 3 (A & B - л).
10 не делится на 2 (A - л). 5 не больше 3 (B - л). 10 делится на 2 и 5 больше 3 (A & B - л).
2) Дизъюнкция двух логических высказываний (или, v) — логическое высказывание, истинное только тогда, когда хотя бы одно из них истинно.
Таблица истинности
Примеры:
10 делится на 2 (A - и). 5 больше 3 (B - и). 10 делится на 2 или 5 больше 3 (A V B - и).
10 не делится на 2 (A - л). 5 больше 3 (B - и). 10 не делится на 2 или 5 больше 3 (A V B - и).
10 делится на 2 (A - и). 5 не больше 3 (B - л). 10 делится на 2 или 5 не больше 3 (A V B - и).
10 не делится на 2 (A - л). 5 не больше 3 (B - л). 10 не делится на 2 или 5 не больше 3 (A V B - л).
3) Инверсия (Отрицание логического высказывания) (НЕ, 
, 
) — логическое высказывание, принимающее значение «истинно», если исходное высказывание ложно, и наоборот.
Таблица истинности:
Пример: Луна — спутник Земли (А). Луна — не спутник Земли ( A).
4) Импликация двух логических высказываний A и B ("если..., то...", 
) — логическое высказывание, ложное только тогда, когда A (условие) истинно, а B (следствие) ложно.
Таблица истинности
|
|
|
Примеры:
Данный четырёхугольник — квадрат (A - и). Около данного четырёхугольника можно описать окружность (B - и). Если данный четырёхугольник квадрат, то около него можно описать окружность (A → B - и).
Данный четырёхугольник — не квадрат (A - л). Около данного четырёхугольника можно описать окружность (B - и). Если данный четырёхугольник не квадрат, то около него можно описать окружность (A → B - и).
Данный четырёхугольник — квадрат (A - и). Около данного четырёхугольника нельзя описать окружность (B - л). Если данный четырёхугольник квадрат, то около него нельзя описать окружность (A → B - л).
Данный четырёхугольник — не квадрат (A - л). Около данного четырёхугольника нельзя описать окружность (B - л). Если данный четырёхугольник не квадрат, то около него нельзя описать окружность (A → B - и).
5) Эквиваленция (Равносильность, эквивалентность) (
) двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны или ложны.
Таблица истинности
Примеры:
24 делится на 6 (A - и). 24 делится на 3 (B - и). 24 делится на 6 тогда и только тогда, когда 24 делится на 3 (A ↔ B - и).
24 не делится на 6 (A - л). 24 делится на 3 (B - и). 24 не делится на 6 тогда и только тогда, когда 24 делится на 3 (A ↔ B - л).
24 делится на 6 (A - и). 24 не делится на 3 (B - л). 24 делится на 6 тогда и только тогда, когда 24 делится на 3 (A ↔ B - л).
24 не делится на 6 (A - л). 24 не делится на 3 (B - л). 24 не делится на 6 тогда и только тогда, когда 24 не делится на 3 (A ↔ B - и).
6) Строгая дизъюнкция истинна только тогда, когда одно высказывание истинно,
а другое ложно.
, 
, 
, 
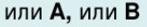
Пример: Сегодня понедельник или вторник.
Таблица истинности
Задача. Заполните таблицу истинности
ЛОГИЧЕСКИЕ ФОРМУЛЫ
|
|
|
