 |
Программа по линейной алгебре
|
|
|
|
Домашнее задание по курсу «Линейная алгебра»
Студенты 1 курса заочного отделения должны выполнить по учебному плану одну контрольную работу своего варианта. Номер варианта совпадает с последней цифрой номера зачетной книжки (если номер заканчивается на цифру «0» тогда следует выполнять вариант номер 10). Номера задач вариантов контрольных заданий указаны в таблице, приведенной ниже:
| номер варианта | Контрольные задания | ||||||||
| 81. | |||||||||
| 82. | |||||||||
| 83. | |||||||||
| 84. | |||||||||
| 85. | |||||||||
| 86. | |||||||||
| 87. | |||||||||
| 88. | |||||||||
| 89. | |||||||||
| 90. |
Титульный лист оформить следует по образцу:
| «РГЭУ (РИНХ)» Факультет _______________ Контрольная работа по дисциплине «____________________» Выполнил(а) студент(ка) _________________________________ Группа № ________________________________________________ Зачетная книжка № _______________________________________ Проверил(а) преподаватель кафедры «Фи ПМ»_______________ 2015 / 16 |
ИТОГОВЫЙ КОНТРОЛЬ ЗНАНИЙ: ЭКЗАМЕН.
Основные требования к итоговому контролю: знание основных понятий теории и умение их применять к решению практических задач
Программа по линейной алгебре
1. Множества и операции над ними. Способы задания множеств. Пространства.
2. Отображения. Композиция отображений. Взаимно-однозначные (биективные) отображения. Обратимые и обратные отображения.
|
|
|
3. Комплексные числа и алгебраические операции над ними. Комплексная плоскость, модуль и аргумент комплексного числа. Тригонометрическая и показательная формы комплексного числа.
4. Многочлены и алгебраические уравнения. Определения. Разложение многочлена. Основная теорема алгебры (теорема Гаусса) и ее следствия. Комплексные корни многочлена с действительными коэффициентами.
5. Системы линейных уравнений. Основные определения: решения, совместность, несовместность, определенность, неопределенность, равносильность систем. Однородные системы. Элементарные преобразования систем (теорема).
6. Методы Гаусса и Жордана-Гаусса решения систем линейных уравнений общего вида. Общее, частное, базисное решения; система, приведенная к единичному базису, базисные и свободные переменные. Ранг системы уравнений, максимальное число базисных решений. Жордановы исключения, их применения к решению систем линейных уравнений и отысканию базисных решений.
7. Матрицы и векторы. Основные определения. Линейные операции над векторами и матрицами. Частные виды матриц: квадратная, диагональная, единичная, строка, столбец. Произведение матриц и его свойства.
8. Операция транспонирования матриц и ее свойства.
9. Обратная матрица и ее построение (метод Жордана-Гаусса)
10. Матричный оператор. Построение матрицы по матричному оператору (лемма). Линейность матричного оператора. Композиция матричных операторов. Обратимость матричного оператора.
11. Матричная форма записи систем линейных уравнений и матричный способ ее решения.
12. Определители. Определители n -ого порядка: определение и основные свойства.
13. Разложение определителя по любому столбцу и дальнейшие свойства определителя. Теорема аннулирования. Транспонирование определителя. Определители специальных матриц.
14. Применение определителей к решению систем линейных уравнений. Теорема (формулы) Крамера.
|
|
|
15. Вырожденная, невырожденная матрицы. Критерий обратимости матрицы. Вычисление обратной матрицы через алгебраические дополнения.
16. Линейные векторные пространства. Определение векторного пространства. Аксиомы и следствия из них. Примеры.
17. Линейная комбинация, линейная оболочка векторов. Линейная зависимость системы векторов: определения и основные свойства.
18. Размерность и базис векторного пространства. Теоремы: о числе элементов базиса, о виде базиса в n -мерном пространстве, о дополнении до базиса. Критерий линейной независимости n векторов в  .
.
19. Координаты вектора в данном базисе. Разложение вектора по базису. Линейные операции над векторами в координатной форме. Изоморфизм векторных пространств (определение, критерий).
20. Переход к новому базису. Матрица перехода от одного базиса к другому. Преобразование координат вектора при переходе к новому базису.
21. Подпространства векторного пространства: определения, примеры.
22. Линейные операторы. Определение линейного оператора, примеры. Образ и ядро линейного оператора, основные свойства.
23. Теорема о структуре множества решений неоднородного линейного уравнения, следствия.
24. Матрица линейного оператора. Однозначное соответствие между матрицей и оператором.
25. Операции над линейными операторами, действующими в фиксированном пространстве: сумма, умножение на число, произведение. Обратный оператор и его матрица.
26. Собственные значения и собственные векторы линейного оператора. Определение, процедура их отыскания. Приведение матрицы линейного операторы к диагональному виду. Линейная независимость собственных векторов, соответствующих различным собственным значениям.
27. Евклидово пространство. Скалярное произведение, примеры скалярного произведения в  . Евклидово векторное пространство. Норма вектора. Неравенство Коши-Буняковского, неравенство треугольника. Угол между векторами. Ортогональные и ортонормированные базисы. Процедура ортогонализации базиса в евклидовом пространстве. Скалярное произведение и норма вектора в ортонормированном базисе.
. Евклидово векторное пространство. Норма вектора. Неравенство Коши-Буняковского, неравенство треугольника. Угол между векторами. Ортогональные и ортонормированные базисы. Процедура ортогонализации базиса в евклидовом пространстве. Скалярное произведение и норма вектора в ортонормированном базисе.
28. Ортогональные подпространства, ортогональность их базисных векторов. Ортогональные дополнения и их свойства.
|
|
|
29. Линейные операторы в евклидовом пространстве. Самосопряженные операторы и их матрицы. Свойства самосопряженного оператора.
30. Линейные функционалы: определения, примеры. Теоремы об общем виде линейных функционалов.
31. Квадратичные формы: определения, примеры. Квадратичная форма в  , ее матрица. Приведение квадратичной формы к сумме квадратов (каноническому виду). Знакоопределенность квадратичных форм.
, ее матрица. Приведение квадратичной формы к сумме квадратов (каноническому виду). Знакоопределенность квадратичных форм.
32. Линейные геометрические объекты. Гиперплоскость в  : общее уравнение; нормальный вектор и его свойства, частные виды уравнений. Прямая в
: общее уравнение; нормальный вектор и его свойства, частные виды уравнений. Прямая в  : параметрическое, каноническое, общее уравнение; уравнение по двум точкам.
: параметрическое, каноническое, общее уравнение; уравнение по двум точкам.
33. Прямая и гиперплоскость в  : углы, условия параллельности и ортогональности гиперплоскостей, прямых и друг с другом.
: углы, условия параллельности и ортогональности гиперплоскостей, прямых и друг с другом.
34. Расстояния между двумя точками, от точки до гиперплоскости. Уравнение отрезка и его середина.
35. Прямая линия на плоскости: общее уравнение и с угловым коэффициентом. Построение прямой линии по общему уравнению.
36. Гиперповерхности уровня линейных функционалов и квадратичных форм.
.
| Вопросы к по Линейной алгебре (Математическое программирование) |
| 1. Выпуклая линейная комбинация векторов в Rn.. Понятие выпуклого множества. Понятие угловой точки выпуклого множества. Теоремы о выпуклых множествах. 2. Понятие полупространства в Rn. Теорема о связи угловых точек области допустимых решений с опорными решениями эквивалентной системы уравнений. 3. Математическая модель задачи линейного программирования. Основные определения: целевая функция, система ограничений, допустимый план, опорный план, оптимальный план. 4. Общая, основная и каноническая формы задач линейного программирования. Переход от одной формы модели к другой. 5. Фундаментальная теорема линейного программирования. Основные выводы, полученные из решения задач графическим методом. 6. Идея симплекс-метода. Симплекс-таблица. Теорема о выборе разрешающего элемента, когда свободные члены системы ограничений неотрицательны. 7. Критерий оптимальности на максимум задачи линейного программирования. 8. Теорема о выборе разрешающего элемента, когда среди свободных членов системы ограничений есть отрицательные. 9. Понятие о вырождении и зацикливании в симплексном методе. 10. Постановка пары взаимно-двойственных задач. Правила построения математической модели двойственной задачи. 11. Теорема о допустимых решениях взаимно-двойственных задач. Основное неравенство теории двойственности. 12. Двойственная симплекс-таблица. Решение двойственной задачи с помощью двойственных симплекс-таблиц. 13. Основные теоремы двойственности. 14. Постановка транспортной задачи и ее математическая модель 15. Особенности математической модели транспортной задачи. 16. Открытая и закрытая модели транспортной задачи. Теорема о разрешимости транспортной задачи. 17. Теорема о ранге системы ограничений транспортной задачи. 18. Методы построения первого опорного плана. 19. Метод потенциалов. Понятие цикла. Основные виды циклов. Перемещение по циклу. 20. Теоремы об опорном плане транспортной задачи. Критерий оптимальности плана транспортной задачи. 21. Теорема о переходе от одного опорного плана к другому в транспортной задаче. 22. Вырождение в транспортной задаче. |
Список рекомендуемой литературы
|
|
|
1. Ильин В.А., Поздняк Э.Г. Линейная алгебра. – М.: Наука. Гл. ред. физ.-мат. лит., 1974. – 296 с.
2. Петрова В.Т. Лекции по алгебре и геометрии: учебник для вузов: в 2х ч. – М.: Гуманит. изд. центр ВЛАДОС, 1999. – Ч.1. – 312 с.
3. Петрова В.Т. Лекции по алгебре и геометрии: учебник для вузов: в 2х ч. – М.: Гуманит. изд. центр ВЛАД ОС, 1999. – Ч.2. – 344 с.
4. Воеводин В.В. Линейная алгебра. – М.: Наука, Гл. ред. физ.-мат. лит., 1980. – 400 с.
5. Мальцев А.И. Основы линейной алгебра. – М.: Наука, Гл. ред. физ.-мат. лит., 1975. – 400 с.
6. Кострикин А.И. Введение в алгебру. – М.: Наука, Гл. ред. физ.-мат. лит., 1977. – 496 с.
7. Беклимишев Д.В. Курс аналитической геометрии и линейной алгебры. – 4-е изд.– М.: Наука, Гл. ред. физ.-мат. лит., 1980. – 336 с.
8. Солопова О.Г. Линейная алгебра. Учебное пособие. Ростов-на-Дону: РГЭУ (РИНХ), 2004, - 190 с.
9. Левендорский С.З. Курс аналитической геометрии (метод. указ.) – Ростов-на-Дону: РИНХ, 1989. – 38 с.
10. Кудрявцев В.А., Демидович Б.Л. Краткий курс высшей математики. – М.: Наука, Гл. ред. физ.-мат. лит., 1985.
11. Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа. Под ред. Ефимова А.В., Демидовича Б.П. – М.: Наука, Гл. ред. физ.-мат. лит., 1981. – 464 с.
12. Карпелевич Ф.И., Садовский Л.Е. Элементы линейной алгебры и линейного программирования. – М.: Наука, Гл. ред. физ.-мат. лит., 1965. – 274 с.
13. Батищева Г.А., Левендорский С.З. Системы линейных уравнений. Матрицы и векторы (методические указания). Ч. 1 – Ростов-на-Дону: РИНХ, 1995. – 45 с.
|
|
|
14. Батищева Г.А., Левендорский С.З. Системы линейных уравнений. Определители. Ч. 2. – Ростов-на-Дону: РГЭА, 1995.
15. Батищева Г.А.,Кисилева Н.Н., Левендорский С.З. Множества. Отображение множеств. Методические указания по изучению курса высшей математики.– Ростов-на-Дону: РИНХ, 1991.
16. Батищева Г.А., Левендорский С.З. Линейные операторы (методические указания). – Ростов-на-Дону: РИНХ, 1992.
17. Батищева Г.А., Левендорский С.З. Евклидово пространство. Линейные функционалы и квадратичные формы (методические указания).– Ростов-на-Дону: РИНХ, 1992.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Задание 1. Решить систему уравнений по формулам Крамера
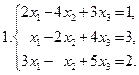
| 
|

| 
|

| 
|

| 
|

| 
|
Задание 2. Решить систему уравнений матричным способом
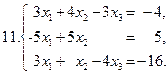
| 
|

| 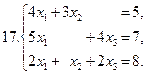
|

| 
|

| 
|

| 
|
Задание 3. Решить систему уравнений методом исключения неизвестных (методом Жордана-Гаусса); найти базисное решение системы.

| 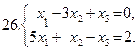
|
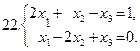
| 
|

| 
|
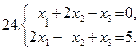
| 
|

| 
|
Задание 4. Показать, что векторы а1, а2, а3 образуют базис в R 3 и разложить вектор а4 по этому базису.
31. а1 = (2; 1; 3), а2 = (-4; -2; -1), а3= (3; 4; 5), а4 = (1; 3; 2).
32. а1 = (2; 1; 4), а2 = (-3; 5; 1), а3= (1; -4; -3), а4 = (2; -5; -4).
33. а1 = (2; 3; 1), а2 = (-1; 2; -2), а3= (1; 2; 1), а4 = (2; -2; 1).
34. а1 = (1; 2; 1), а2 = (2; -1; 3), а3= (3; -1; 4), а4 = (5; 1; 6).
35. а1 = (2; 2; -1), а2 = (0; 4; 8), а3= (-1; -1; 3), а4 = (1; 1; 2).
36. а1 = (1; -2; 1), а2 = (1; 1; 1), а3= (-1; 1; 1), а4 = (2; 3; 6).
37. а1 = (3; -2; 2), а2 = (-1; 1; -1), а3= (0; 1; 4), а4 = (5; 0; 15).
38. а1 = (5; 1; 4), а2 = (0; -1; 1), а3= (4; 2; 2), а4 = (1; 0; 1).
39. а1 = (2; 3; 1), а2 = (2; 2; 1), а3= (-1; -3; -2), а4 = (4; 7; 3).
40. а1 = (2; -1; 4), а2 = (1; -2; 2), а3= (-1; 2; 1), а4 = (-4; 14; 7).
Задание 5. Дан треугольник с вершинами A(x 1, y 1), B(x 2, y 2), C(x 3, y 3). Найти:
(а) уравнение стороны АС;
(б) уравнение высоты АК;
(в) длину средней линии MP(параллельно стороне BC);
(г) угол  ^
^  ;
;
(д) точку пересечения высот треугольника.
41. А (-4,0), B (-2,6), C (2,2).
42. A (-3,0), B (-1,6), C (3,2).
43. A (-2,0), B (0,6), C (4,2).
44. A (-1,0), B (1,6), C (5,2).
45. A (0,0), B (2,6), C (6,2).
46. A (1,0), B (3,6), C (7,2).
47. A (2,0), B (4,6), C (8,2).
48. A (3,0), B (5,6), C (9,2).
49. A (4,0), B (6,6), C (10,2).
50. A (-5,0), B (-1,6), C (1,2).
Задание 6. Найти:
а) уравнение прямой  , проходящей через точки А(x 1, y 1, z 1); B(x 2, y 2, z 2).
, проходящей через точки А(x 1, y 1, z 1); B(x 2, y 2, z 2).
б) уравнение плоскости  , проходящей через точку С(0, y 3, 1) перпендикулярно прямой
, проходящей через точку С(0, y 3, 1) перпендикулярно прямой  .
.
в) уравнение плоскости, проходящей через три точки А(x 1, y 1, z 1); B(x 2, y 2, z 2), С(0, y 3, 1)
г) точку пересечения прямой  с плоскостью H: a x +b y +c z +1=0.
с плоскостью H: a x +b y +c z +1=0.
51. A(1,2,3), B(3,4,4), C(0,-3,1), H: 3 x + y +2 z +1=0.
52. A(1,1,2), B(3,2,3), C(0,-4,1), H: 2 x + y + z +1=0.
53. A(1,1,1), B(3,3,2), C(0,-4,1), H: x + y + z +1=0.
54. A(1,1,3), B(3,2,4), C(0,-4,1), H: 3 x + y + z +1=0.
55. A(2,1,1), B(5,2,2), C(0,-4,1), H: x +2 y + z +1=0.
56. A(2,2,1), B(5,4,2), C(0,-3,1), H: x +2 y +2 z +1=0.
57. A(3,2,1), B(7,4,2), C(0,-3,1), H: x +3 y +2 z +1=0.
58. A(3,2,2), B(7,4,2), C(0,-3,1), H: 2 x +3 y +2 z +1=0.
59. A(4,1,1), B(9,2,2), C(0,-4,1), H: x +4 y + z +1=0.
60. A(4,2,1), B(9,4,2), C(0,-3,1), H: x +4 y +2 z +1=0.
Задание 7. Решить графическим и симплексным методом задачу линейной оптимизации
61.  62.
62. 


63.  64.
64. 


65. 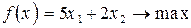 66.
66. 


67. 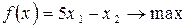 68.
68. 


69.  70.
70. 


Задание 8. Решить транспортную задачу. Найти оптимальный план.
71. Ai =(110,110,80)
Bj =(50,90,90,70)
C= 
72. Ai =(60,80,100)
Bj =(40,60,80,60)
C= 
73. Ai =(12,5,18)
Bj =(10,11,8,6)
C= 
74. Ai =(60,70,20)
Bj =(40,30,30,50)
C= 
75. Ai =(200,400,600)
Bj =(100,300,400,400)
C= 
76. Ai =(200,160,120)
Bj =(120,120,160,80)
C= 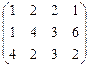
77. Ai =(180,220,220)
Bj =(140,180,180,100)
C= 
78. Ai =(180,50,120)
Bj =(60,110,80,100)
C= 
79. Ai =(40,140,120)
Bj =(100,60,60,80)
C= 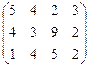
80. Ai =(120,80,40)
Bj =(80,60,80,20)
C= 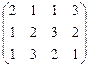
|
|
|


