 |
Уравнение для температуры с переменными свойствами
|
|
|
|
Уравнение баланса энтальпии
В этом разделе мы выведем трехмерное уравнение баланса энтальпии в движущейся жидкости.
Уравнение баланса энтальпии
Рассмотрим изменение энтальпии 
единицы массы жидкости в выделенном объеме 
(рис.1). Изменение энтальпии складывается из потока энтальпии через поверхность 
, ограничивающую выделенный объем и в результате действия внутри объема источников энергии
.
Здесь 
– плотность жидкости, 
– поток энтальпии, 
– вектор нормали к поверхности,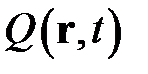 
– источник энергии на единицу массы.
Рис. 1. К выводу уравнения баланса энтальпии.
Знак минус в уравнении баланса ставится исходя из физических соображений. Вектор потока, направленный по вектору нормали к поверхности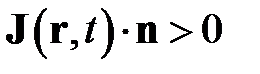 
приводит к уменьшению энтальпии в объеме 
.
Энтальпия является функцией температуры среды 
,
где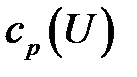 
– изобарическая теплоемкость.
Температура среды меняется в объеме и во времени 
, что приводит в соответствии с формулой к зависимости энтальпии и теплоемкости от времени и координат 
, 
.
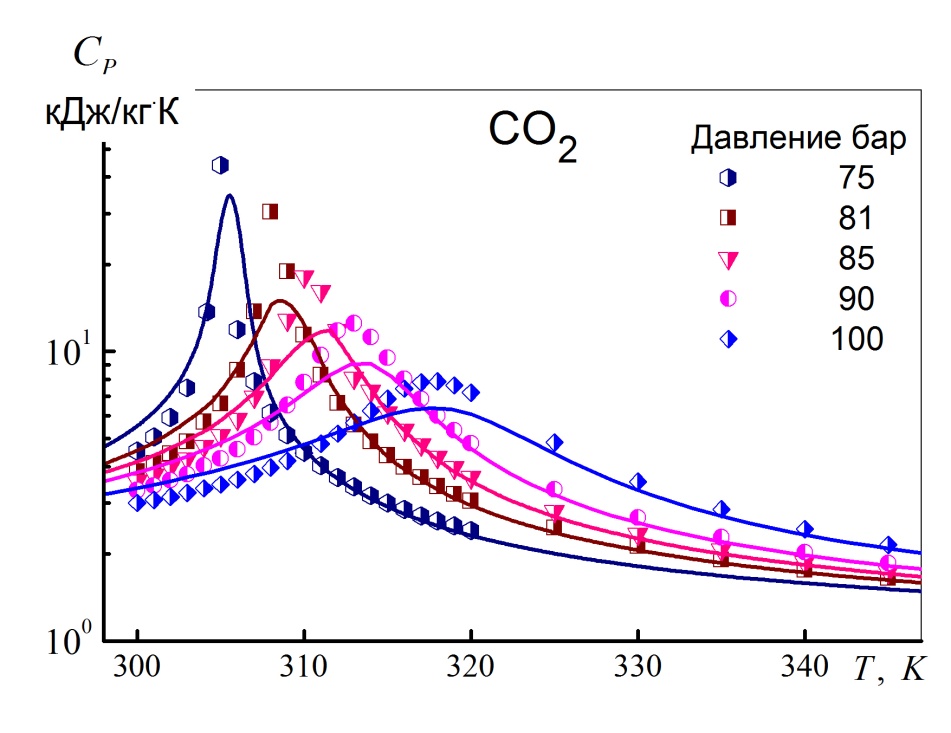
Рис. 2. Иллюстрация изменения теплоемкости и плотности диоксида углерода. вблизи термодинамического критического состояния.
Уравнение представляет интегральный баланс энтальпии. В уравнении привлекаем формулу Остроградского-Гаусса
.
Уравнение баланса принимает следующий вид
.
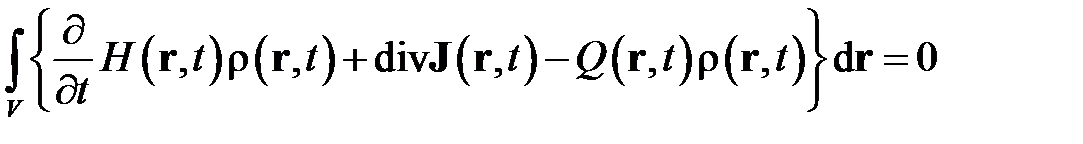Используя предположение о произвольности выбранного объема 
, получаем уравнение баланса энтальпии в дифференциальном виде
.
|
|
|
Поток энтальпии складывается из конвективного переноса 
за счет движения жидкости со скоростью 
и потока энтальпии за счет молекулярной теплопроводности 
.
Перенос энтальпии за счет движения жидкости равен
.
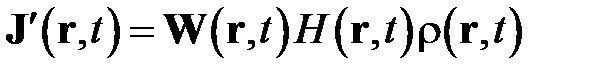Для моделирования переноса тепла за счет молекулярного хаотического движения используем гипотезу Фурье: поток тепла направлен в сторону уменьшения температуры среды 
и пропорционален коэффициенту молекулярной теплопроводности 
.
Коэффициент теплопроводности также является функцией температуры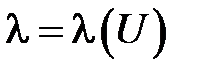 
. Для неизотермических условий коэффициент теплопроводности зависит от координат и времени 
.
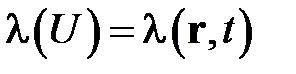Из формул и вытекает уравнение баланса энтальпии в виде
.
Для раскрытия слагаемых в левой части последнего уравнения привлекаем уравнение баланса массы жидкости
.
В результате дифференцирования по частям, записываем следующее выражение
.
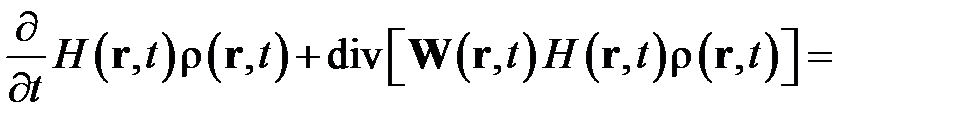
При вычислении производных от энтальпии используем формулу
, 
.
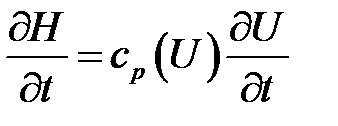В результате из формулы вытекает дифференциальное уравнение для температуры жидкости
.
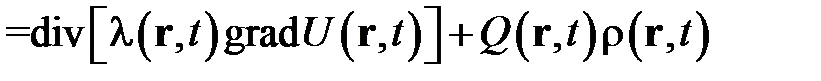Уравнение для температуры справедливо в общем случае для сжимаемой среды с переменными свойствами. В случае постоянных свойств уравнение принимает вид
,
где 
– коэффициент температуропроводности.
Уравнение принадлежит параболическому типу линейных уравнений второго порядка с частными производными.
|
|
|
Для неподвижной среды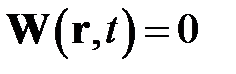 
уравнение принимает простой вид
.
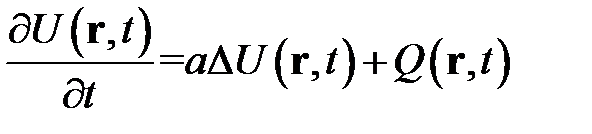Уравнение для температуры с переменными свойствами
Приведем уравнение баланса энтальпии с переменными свойствами к каноническому виду, который используется для анализа нелинейных эффектов при диффузии тепла. Для неподвижной среды с постоянной плотностью уравнение принимает вид
.
Градиент энтальпии записывается через градиент температуры
.
Уравнение принимает вид
.
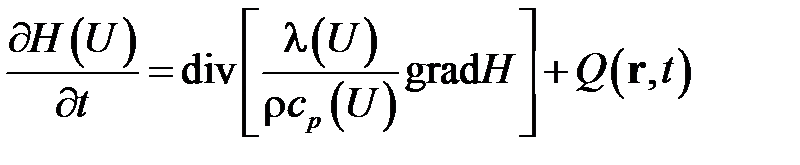Энтальпия – монотонная функция от температуры. По заданному значению энтальпии однозначно определяются температура, а также теплоемкость и коэффициент теплопроводности, которые являются растущими функциями от температуры. Таким образом, коэффициент температуропроводности в уравнении 
является функцией энтальпии. С учетом сделанного замечания уравнение является уравнением для энтальпии с переменным коэффициентом диффузии тепла
.
Предполагая, что теплоемкость материала слабо зависит от температуры, можем записать уравнение в виде уравнения нелинейной теплопроводности
.
На основе уравнения иллюстрируются эффекты локализации тепла в среде с нелинейным коэффициентом диффузии 
.
|
|
|
