 |
Задачи контрольной работы № 1(математический анализ)
|
|
|
|
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Задача 1
Найти предел:

 3x2 + 11x + 10 x – 1 3 – x/2
3x2 + 11x + 10 x – 1 3 – x/2

 а) lim; г) lim;
а) lim; г) lim;
x→ -2  -
-  x→∞ x + 3
x→∞ x + 3
x (sin 5x + sin 6x) lg (x + 1)

 б) lim; д) lim;
б) lim; д) lim;
x→0  x→0 sin 2x
x→0 sin 2x
tg2 3x
 в) lim; е) lim (e3x – e2x) ∙ ctg 4x
в) lim; е) lim (e3x – e2x) ∙ ctg 4x
x→0  x→0
x→0
Решение:
а) Функция, предел которой при х→ -2 требуется найти, представляет собой частное двух функций. Однако применить теорему о пределе частного ([2], гл.6. § 5 теорема4) в данном случае нельзя, так как предел функции, стоящей в знаменателе, при х→ -2 равен нулю.
Преобразуем данную функцию, умножив числитель и знаменатель дроби, находящейся под знаком предела, на выражение  , сопряженное знаменателю. Параллельно разложим квадратный трехчлен в числителе на линейные множители:
, сопряженное знаменателю. Параллельно разложим квадратный трехчлен в числителе на линейные множители:
3х2 + 11х + 10 (3х + 5)(х + 2)( )
)

 = =
= =
 (
( )(
)( )
)
(3х + 5)(х + 2)( ) (3х +5)(х + 2)(
) (3х +5)(х + 2)( )
)

 =.
=.
(х + 7) – (3 – х) 2(х + 2)
Сокращая теперь числитель и знаменатель последней дроби на общий множитель х + 2, получим новую функцию (3х + 5)( )
)
 у =,
у =,
которая отличается от данной значением лишь в одной точке х = -2: данная функция в этой точке не определена, а новая определена и непрерывна как элементарная функция ([2], гл.5, § 3). Поскольку переопределение функции в одной точке не сказывается на значении предела и поскольку для функции, непрерывной в точке х0, ее предел при х→х0 равен значению этой функции в точке х0 ([2], гл.6, §7), то
3x2 + 11x + 10 (3х + 5)( ) (3 ∙ (-2) + 5)(
) (3 ∙ (-2) + 5)(


 lim = lim = = -
lim = lim = = -  .
.
x→-2  x→-2 2 2
x→-2 2 2
б) И в этом примере начнем преобразования с умножения числителя и знаменателя дроби, стоящей под знаком предела, на выражение, сопряженное к знаменателю:
х(sin 5x + sin 6x) x(sin 5x + sin 6x)( )
)

 = =
= =
 (1 + x ∙ tg x) – (1 - x ∙ tg x)
(1 + x ∙ tg x) – (1 - x ∙ tg x)
x(sin 5x + sin 6x)( ) (sin 5x + sin 6x)(
) (sin 5x + sin 6x)( )
)

 = = =
= = =
2x ∙ tg x 2x ∙ tg x
sin 5x + sin 6x cos x

 = ∙ ∙ (
= ∙ ∙ ( ).
).
sin x 2
|
|
|
Заметим, что пределы в нуле второго и третьего сомножителей как непрерывных в нуле функций равны их значениям в этой точке:
cos x
 lim = ½; lim (
lim = ½; lim ( ) = 2
) = 2
x→0 2 x→0
Чтобы найти предел первого сомножителя, разделим его числитель и знаменатель на х:
sin 5x + sin 6x sin 5x sin 6x


 +
+
sin 5x + sin 6x x x x


 = =
= =

 sin x sin x sin x
sin x sin x sin x
x x
Предел sin x
 lim = 1
lim = 1
x→0 x
есть первый замечательный предел ([2], гл.6, § 6). Пределы  легко
легко
сводятся к нему. Например, 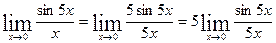
и после замены t = 5х:
sin 5x sin t

 lim = lim = 1
lim = lim = 1
x →0 5x x →0 t
sin 5x sin 6x

 Следовательно, lim = 5. Аналогично, lim = 6. Теперь с помощью теорем о пре-
Следовательно, lim = 5. Аналогично, lim = 6. Теперь с помощью теорем о пре-
x →0 x x →0 x
деле частного и суммы ([2], гл.6, § 5, теорема 2,4) вычисляем предел первого сомножителя:
sin 5x sin 6x

 lim + lim
lim + lim
sin 5x + sin 6x x →0 x x →0 x 5 + 6


 lim = = = 11
lim = = = 11
x →0 sin x sin x 1
 lim
lim
x →0 x
Воспользовавшись, наконец, теоремой о пределе произведения ([2], гл. 6, § 5, теорема 3), окончательно получаем: sin 5x + sin 6x cos x

 lim ∙ ∙ (
lim ∙ ∙ ( ) = 11∙ ½ ∙ 2 = 11
) = 11∙ ½ ∙ 2 = 11
x →0 sin x 2
в) Избавляясь от иррациональности в знаменателе (так же, как и в предыдущих двух примерах) и применяя формулу 1 – cos 2x = 2sin2x, будем иметь:
tg23x tg23x ∙ ( )
)

 lim = lim =
lim = lim =
x →0  x →0 2 – (3 – cos 2x)
x →0 2 – (3 – cos 2x)
tg23x tg23x

 = lim (
= lim ( ) = lim (
) = lim ( )
)
x →0 cos 2x – 1 x →0 - 2sin2x
Предел в нуле функции у =  найдем, воспользовавшись непрерывностью этой элементарной функции в нуле:
найдем, воспользовавшись непрерывностью этой элементарной функции в нуле:
lim ( ) =
) = 
tg23x
 Предел в нуде функции у = найдем, разделив предварительно числитель и зна-
Предел в нуде функции у = найдем, разделив предварительно числитель и зна-
-2sin2x
менатель дроби в правой части равенства на х2 и используя основные свойства предела:



 tg23x tg3x 2 sin 3x 2
tg23x tg3x 2 sin 3x 2


 lim lim
lim lim
tg23x x2 x →0 x x →0 x cos 3x






 lim = - ½ ∙ lim = - ½ ∙ = - ½ ∙ =
lim = - ½ ∙ lim = - ½ ∙ = - ½ ∙ =
 x →0 -2sin2x x →0 sin2x sin x 2 sin x 2
x →0 -2sin2x x →0 sin2x sin x 2 sin x 2

 x2 lim lim
x2 lim lim
x →0 x x →0 x

 sin 3x 3 2
sin 3x 3 2

 lim ∙
lim ∙



 x →0 3x cos 3x sin 3x 3 2 3 2
x →0 3x cos 3x sin 3x 3 2 3 2



 = - ½ ∙ = - ½ ∙ lim ∙ lim = - ½ ∙ 1 ∙ = - 9/2
= - ½ ∙ = - ½ ∙ lim ∙ lim = - ½ ∙ 1 ∙ = - 9/2
12 x →0 3x x →0 cos 3x cos 0
Теперь, применяя теорему о пределе произведения, получим:
tg23x tg23x

 lim = lim ∙ lim (
lim = lim ∙ lim ( ) =
) = 
x →0  x →0 -2 sin2 x x →0
x →0 -2 sin2 x x →0
г) Прежде всего преобразуем основание данной степенно-показательной функции:
|
|
|
х – 1 х + 3 – 3 – 1 (х + 3) – 4 4



 = = =1-
= = =1-
х + 3 х + 3 х + 3 х + 3
4 х + 3 1 4 4




 Введем новую переменную t = -. Тогда - =, х + 3 = -, х = -3 -.
Введем новую переменную t = -. Тогда - =, х + 3 = -, х = -3 -.
х + 3 4 t t t
Заметим, что предел функции t при х→+∞ равен нулю, то есть t→0 при х→+∞.
Следовательно, 
В конце мы воспользовались теоремой о пределе произведения, следствием теоремы о пределе сложной функции ([2], гл.6, § 5), вторым замечательным пределом ([2], гл.6, §6) и непрерывностью в нуле функции у = (1 + t)9/2
д) Разделим числитель и знаменатель дроби, стоящей под знаком предела, на х:
lg (x + 1)
 lg (x + 1) x
lg (x + 1) x

 =
=
sin 2x sin 2x
 x
x
и рассмотрим пределы в нуле числителя и знаменателя получившейся большой дроби:
 lg (x + 1) 1
lg (x + 1) 1

 lim = lim tg (x + 1) = lim lg (x + 1)1/ x = lg lim (x + 1)1/ x = lg e
lim = lim tg (x + 1) = lim lg (x + 1)1/ x = lg lim (x + 1)1/ x = lg e
x →0 x x →0 x x →0 x →0
и sin 2x 2sin 2x sin 2x


 lim = lim = 2 ∙ lim = 2 ∙ 1 = 2.
lim = lim = 2 ∙ lim = 2 ∙ 1 = 2.
x →0 x x →0 2x x →0 2x
Используя, наконец, теорему о пределе частного, получим:
lg (x + 1) lg (x + 1)

 lim
lim
x x →0 x lg e


 lim = =
lim = =
x →0 sin 2x sin 2x 2

 x lim
x lim
x →0 x
е) Представим выражение под знаком предела в виде
ex – 1
 cos 4x ex – 1 x
cos 4x ex – 1 x


 (e3x – e2x ) ∙ ctg 4x = (e2x ex – e2x) ∙ = e2x ∙ ∙ cos 4x = e2x ∙ ∙ cos 4x
(e3x – e2x ) ∙ ctg 4x = (e2x ex – e2x) ∙ = e2x ∙ ∙ cos 4x = e2x ∙ ∙ cos 4x
sin 4x sin 4x sin 4x
 x
x
Легко находим: lim e2x = e0 = 1; lim cos 4x = cos 0 = 1;
x →0 x →0
sin 4x 4sin 4x sin 4x


 lim = lim = 4 ∙ lim = 4 ∙ 1 = 4
lim = lim = 4 ∙ lim = 4 ∙ 1 = 4
x →0 x x →0 4x x →0 4x
ех - 1
 Для вычисления предела функции у = при x →0 введем новую переменную
Для вычисления предела функции у = при x →0 введем новую переменную
х
t = ex – 1. Тогда ех = t + 1, x = ln (1 + t) причем предел в нуле непрерывной функции t = ex – 1 равен значению функции в нуле: е0 – 1 = 1 – 1 = 0, то есть t→0 при x →0. Следовательно,
lim 1
 ex – 1 t 1 x →0 1 1
ex – 1 t 1 x →0 1 1






 lim = lim = lim = = = = 1
lim = lim = lim = = = = 1
x →0 x x →0 ln (1 + t) x →0 1/t ln (1 + t) lim ln (1 + t)1/ t ln lim (1 + t)1/ t ln e
x →0 x →0
Применяя теоремы о пределе произведения и частного, окончательно получаем:
 ex – 1
ex – 1
 x
x
 lim e2x ∙ ∙ cos 4x = 1∙ ¼ ∙ 1 = ¼
lim e2x ∙ ∙ cos 4x = 1∙ ¼ ∙ 1 = ¼
x →0 sin 4x
 x
x
Задача №2
Найти производную функции:
х7(1 – х)9 1 + x√2 + x2

 а) у =; в) у = ln;
а) у =; в) у = ln;
1 + х 1 - x√2 + x2
x√2
 б) y =
б) y =  ; г) y = arctg.
; г) y = arctg.
1 – x2
Решение:
а) Функция представляет собой частное двух функций. Ее производная по правилу дифференцирования частного ([2], гл. 7, § 3, формула 7.15) равна:
 х7(1 – х)9 / (х7(1 – х)9)/ (1 + х) - х7(1 – х)9 (1 + х)/
х7(1 – х)9 / (х7(1 – х)9)/ (1 + х) - х7(1 – х)9 (1 + х)/

 у/ = =
у/ = =
1 + х (1 + х)2
Выражение х7(1 – х)9 есть произведение двух функций х7 и (1 – х)9 . Применяя правило дифференцирования произведения ([2], гл. 7, §3, формула 7.12), имеем:
|
|
|
(х7(1 – х)9)/ = (х7) ∙ (1 – х)9 + х7 ∙ ((1 – х)9)/
Производная (х7)/ = 7х6 ([2], гл. 7, §3, формула 7.8). Функция (1 – х)9 есть сложная функция, поэтому ее производная ([2], гл. 7, §4, формула 7.16) равна:
((1 – х)9)/ = 9(1 – х)8 (1 –х)/ = 9(1 – х)8 ((1)/ - (х)/) = 9(1 – х)8 (0 – 1) = -9(1 – х)8
Производную функции (1 – х) нашли, используя формулы  .
.
Аналогично, (1 + х)/ = 0 + 1 = 1.
Собирая все результаты, получим:
(7х6(1 – х)9 – х7 9(1 – х)8) (1 + х) – х7(1 – х)9 х6(1 – х)8 (7 – 10х – 15х2)

 у = =
у = =
(1 + х)2 (1 + х)2
б) Преобразуем нашу функцию
у = 
Это сложная функция. Взяв за аргумент и = 1 + tg35x и применяя последовательно формулы ([2], гл. 7, §3,4, формулы 7.20, 7.11), получим:

у/ =  / =
/ = 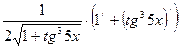 =
= 
Снова, применяя формулу 7.16 (с аргументом и = tg 5x) и формулы 7.19, 7.30 ([2], гл. 7,
§ 3,4), имеем:
1 15 tg25x

 (tg35x)/ = 3 tg25x (tg 5x)/ = 3 tg25x (5x)/ =
(tg35x)/ = 3 tg25x (tg 5x)/ = 3 tg25x (5x)/ =
cos25x cos25x
Окончательно получим:
15 tg25x
 у/ =
у/ =
2  ∙ cos25x
∙ cos25x
в) Наша функция есть сложная логарифмическая, в которой аргументом является выра-
1 + х√2 + х2
 жение и =. Применив формулу 7.16 ([2], гл. 7, §4), получим:
жение и =. Применив формулу 7.16 ([2], гл. 7, §4), получим:
1 - х√2 + х2
 | |||
 |
1 + х√2 + х2 / 1 1 + х√2 + х2 /


 у/ = ln =
у/ = ln =
1 - х√2 + х2 1 + х√2 + х2 1 - х√2 + х2
 1 - х√2 + х2
1 - х√2 + х2
 Далее нам нужно найти производную частного двух функций по формуле 7.15([2], гл. 7,
Далее нам нужно найти производную частного двух функций по формуле 7.15([2], гл. 7,
§ 3), имеем:
1 + х√2 + х2 / (1 + х√2 + х2)/ (1 - х√2 + х2 ) – (1 + х√2 + х2)(1 - х√2 + х2)/

 = =
= =
1 - х√2 + х2 (1 - х√2 + х2)2
(√2 + 2х)(1 – х√2 + х2) – (1 + х√2 + х2)(√2 + 2х) 2√2 - 2√2х2

 = =
= =
(1 – х√2 + х2)2 (1 – х√2 + х2)2
Окончательно получим:
1 – х√2 + х2 2√2 - 2√2х2 2√2 (1 – х2) 2√2 (1 – х2)



 у/ = ∙ = =
у/ = ∙ = =
1 + х√2 + х2 (1 – х√2 + х2)2 (1 + х2)2 – (х√2)2 1 + х4
х√2
 г) По формуле 7.16 ([2], гл. 7, §4), приняв за аргумент выражение и =,
г) По формуле 7.16 ([2], гл. 7, §4), приняв за аргумент выражение и =,

 получим: 1 – х2
получим: 1 – х2
x√2 / 1 x√2 /


 у/ = arctg =
у/ = arctg =
 1 – x2 x√2 2 1 – x2
1 – x2 x√2 2 1 – x2
 1 +
1 +
1 – x2
Воспользовавшись формулой производной для частного двух функций и делая необходимые преобразования, получим:
1 (x√2)/ (1 – х2) - x√2 (1 – х2)/ (1 – х2)2 √2 (1 – х2) - х√2 (-2х)



 у/ = ∙ = ∙ =
у/ = ∙ = ∙ =
(x√2)2 (1 – х2)2 (1 – х2)2 + 2х2 (1 – х2)2
 1 +
1 +
(1 – х2)2
√2 - √2х2 + 2√2х2 √2 (1 + х2)
|
|
|

 = =
= =
1 – 2х2 + х4 + 2х2 1 + х4
Задача 3
23x + 8
 Вычислить приближенное значение функции f (x) = ln в точке х1 = 0,023,
Вычислить приближенное значение функции f (x) = ln в точке х1 = 0,023,
7х + 8
заменив приращение функции в точке х0 = 0 ее дифференциалом.
Решение
Если приращение аргумента ∆х = х1 – х0 достаточно мало по абсолютной величине, то приращение функции ∆f = f (x1) – f (x0) приближенно равно дифференциалу функции df. Поэтому справедлива формула 9.5 ([2], гл.9, §2)
f (x0 + ∆x) ≈ f (x0) + f / (x0) ∆x.
23x + 8
 Для вычисления приближенного значения функции у = ln в точке х1 = 0,023
Для вычисления приближенного значения функции у = ln в точке х1 = 0,023
7х + 8
вычислим производную этой функции в точке х0 = 0:
 23x + 8 / 128
23x + 8 / 128

 f / (x) = ln =;
f / (x) = ln =;
7х + 8 (23x + 8)(7x + 8)
f / (x) = f / (0) = 128 / 64 = 2
Подставив в формулу 9.2, получим:
f (0,023) ≈ ln 1 + 0,023 ∙ 2 = 0,046.
Задача 4
5х + 9
 Исследовать функцию у = и построить ее график.
Исследовать функцию у = и построить ее график.

Решение
1. Область определения данной функции – вся числовая ось, то есть интервал (-∞; +∞), так как выражение 5х + 9
 f (x) =
f (x) =

в правой части аналитического задания функции имеет смысл при любом действительном х.
2. Как элементарная функция данная функция является непрерывной в каждой точке своей области определения, то есть в каждой точке числовой оси.
3. Найдем все асимптоты графика данной функции.
Вертикальных асимптот график данной функции у = f (x) не имеет, поскольку последняя непрерывна на всей числовой оси ([2], гл.8, § 7).
Для отыскания наклонной асимптоты при х→+∞ вычислим следующие два предела
k = lim y/x и b = lim (y – kx)
x→+∞ x→+∞
Если оба они существуют и конечны, то прямая у = kx + b является наклонной асимптотой при х→+∞ графика функции у = f (x) ([2], гл. 9, § 7).
Прежде чем обращаться к вычислению указанных пределов, напомним тождество  *
*
Приступая к вычислению первого предела, разделим числитель и знаменатель дроби на х2, затем воспользуемся равенством (*) и основными свойствами предела:
5x + 9 5 9 5 9




 + +
+ +
y 5x + 9 x2 x x2 x x2 5 ∙ 0 + 9 ∙ 0





 k = lim = lim = lim = lim = lim = = 0
k = lim = lim = lim = lim = lim = = 0
x→+∞ x x→+∞ x√x2 + 3 x→+∞ x√x2 + 3 x→+∞ √x2 + 3 x→+∞ √1 + 3/x2 √ 1+ 3 ∙ 0

 x2 x
x2 x
Для вычисления второго предела разделим числитель и знаменатель дроби на х и, действуя далее аналогично тому, как и при вычислении первого предела, получим:
5x + 9
 5x + 9 x 5 + 9/x 5 + 9 ∙ 0
5x + 9 x 5 + 9/x 5 + 9 ∙ 0



 b = lim (y – kx) = lim y = lim = lim = lim = = 5
b = lim (y – kx) = lim y = lim = lim = lim = = 5
x→+∞ x→+∞ x→+∞ √x2 + 3 x→+∞ √x2 + 3 x→+∞ √1 + 3/x2 √1 + 3 ∙ 0
 x
x
Следовательно, прямая у = 5 является наклонной асимптотой графика данной функции при х→+∞ (поскольку угловой коэффициент k этой прямой равен нулю, то такую наклонную асимптоту называют также горизонтальной при х→+∞).
Для отыскания наклонной асимптоты при х→-∞ вычислим пределы
|
|
|
k1 = lim y/x и b1 = lim (y – kx)
х→+∞ х→+∞
Если оба они существуют и конечны, то прямая y = k1x + b1 является наклонной асимптотой при х→-∞.
Для вычисления этих пределов используем те же приемы, что и выше, учитывая только на сей раз, что  . Теперь, в частности, для отрицательных значений аргумента имеем:
. Теперь, в частности, для отрицательных значений аргумента имеем:
√х2 + 3 √х2 + 3 х2 + 3 3



 = = -√ = - √ 1 +
= = -√ = - √ 1 +
х -√х х2 х2
и следовательно, k1 = 0, b1 = -5

|
то есть наклонной (горизонтальной) асимптотой при х→-∞ на сей раз является прямая у = -5. Изобразим пунктиром найденные асимптоты на предварительном чертеже (рисунок2):
Рисунок 2
4. Найдем точки пересечения графика данной функции с осями координат и установим участки ее знакопостоянства.
Для отыскания абсцисс точек пересечения графика с осью ОХ решим уравнение
5х + 9
 = 0
= 0

Его единственным решением, очевидно, является х = -1,8. Причем, в силу положительности знаменателя при любом х ясно, что
f (x) > 0 при х > -1,8
f (x) < 0 при х < -1,8
Таким образом, точка А (-1,8; 0) является единственной точкой пересечения графика функции с осью ОХ, а для х из интервалов (-∞; -1,8) и (-1,8; +∞) соответствующие точки графика функции расположены, соответственно, ниже и выше оси абсцисс.
Точка пересечения графика функции у = f (x) с осью ОУ – это всегда точка (0; f(0)), если только нуль входит в область определения функции. В нашем случае такой точкой является
В (0; 9/√3), где 9/√3= 9√3/3 = 3√3 ≈ 5,20.
Полученные в результате исследования точки А и В изобразим на предварительном чертеже (рисунок 2)
5. Приступим теперь к отысканию точек экстремума данной функции и участков ее монотонности.
Вычислим сначала ее производную:
5√х2 + 3 – (5х + 9) х
 √х2 + 3 5(х2 + 3) – х(5х + 9) 3(5 –3х)
√х2 + 3 5(х2 + 3) – х(5х + 9) 3(5 –3х)


 у/ = = =
у/ = = =
х2 + 3 (х2 + 3) √х2 + 3 (х2 + 3) ½
Решая уравнение у/ = 0, получим единственный корень производной: х = 5/3 ≈ 1,67
Таким образом, необходимое условие экстремума ([2], гл.8,§ 4) выполняется лишь в точке
х = 5/3. Эта точка разбивает ось абсцисс на два интервала (-∞; 5/3) и (5/3; +∞)
знакопостоянства производной. Для определения знака производной в каждом интервале (пользуясь ее непрерывностью) определим знак производной в одной какой-либо точке каждого интервала. Так как 15 -3

 f/(0) = > 0 и f/(2) = < 0
f/(0) = > 0 и f/(2) = < 0
√27 √343
то заключаем, что функция возрастает на интервале (-∞; 5/3) и убывает на интервале (5/3; +∞), и значит точка х = 5/3 является точкой максимума данной функции ([2], гл.8 § 4). Значение функции в этой точке (то есть максимум функции) равно
5 ∙ 5/3 + 9 52

 f (5/3) = = = √52 ≈ 7.21
f (5/3) = = = √52 ≈ 7.21
√(5/3)2 + 3 √52
Отметим на чертеже вершину С (5/3; √52) графика данной функции (рисунок 2).
6. Наконец, обратимся к исследованию данной функции на выпуклость, вогнутость и существование точек перегиба.
С этой целью найдем производную второго порядка данной функции:
-3(х2 + 3)3/2 – (5 – 3х) ∙ 3/2 ∙ (х2 + 3) ½ ∙ 2х 3(х2 + 3) ½ [-(х2 + 3) – х(5 – 3х)]

 у/ = (у)/ = 3 ∙ = 3 ∙ =
у/ = (у)/ = 3 ∙ = 3 ∙ =
(х2 + 3)3 (х2 + 3)3
9(2х2 – 5х – 3)
 =
=
(х2 + 3)5/2
Решая затем уравнение у// = 0, эквивалентное квадратному уравнению 2х2 – 5х – 3 = 0, находим его корни: х1 = -0,5; х2 = 3, которые разбивают область определения функции на три интервала знакопостоянства второй производной: (-∞; -0,5), (-0,5; 3), (3; +∞). Для определения знака производной второго порядка в каждом из этих интервалов определим ее знак в какой-либо точке соответствующего интервала:
9 ∙ (2 + 5 - 3)
 f//(-1) = = 9/8 > 0
f//(-1) = = 9/8 > 0
√(1 + 3)5
9 ∙ (-3) 27 3


 f//(0) = = - = - = -√3 < 0
f//(0) = = - = - = -√3 < 0
√35 9√3 √3
9 ∙ (32 – 20 – 3) 81

 f//(4) = = > 0
f//(4) = = > 0
√195 192 √19
Из полученных неравенств вытекает, что график функции является выпуклым на интервале
(-0,5; 3) и вогнутым на интервалах (-∞; -0,5) и (3; +∞) ([2], гл.8 § 6), и значит точки
D (-0,5; f(-0.5)) и Е (3; f(3)), согласно определению ([2], гл.8 § 6), являются точками перегиба графика данной функции. Осталось найти ординаты этих точек:
-5/2 + 9 13

 f (-0,5) = = = √13 ≈ 3,61
f (-0,5) = = = √13 ≈ 3,61
√1/4 + 3 √13
15 + 9 24 12


 f (3) = = = = 4√3 ≈ 6,93
f (3) = = = = 4√3 ≈ 6,93
√9 + 3 2√3 √3
Точки D и E также отметим на рисунке 2.
Учитывая результаты полного исследования, соединим непрерывной кривой все ранее отмеченные точки предварительного чертежа так, чтобы эта кривая слева и справа неограниченно приближалась к асимптотам у = -5 и у = 5, соответственно (рисунок3)
Рисунок 3 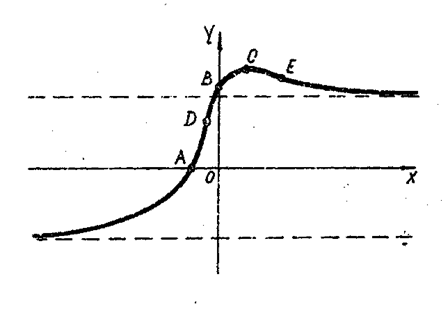
Задачи контрольной работы № 1(математический анализ)
Задачи 1-20
Найти предел:
1.
а)  в)
в) 
б)  г)
г) 
2.
а)  в)
в) 
б)  г)
г) 
3.
а)  в)
в) 
б)  г)
г) 

4.
а) 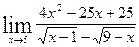 в)
в) 
б)  г)
г) 
5.
а) 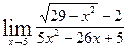 в)
в) 
б)  г)
г) 
6.
а) 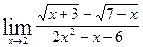 в)
в) 
б)  г)
г) 
7.
а)  в)
в) 
б)  г)
г) 
8.
а) 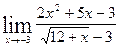 в)
в) 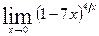
б)  г)
г) 

9.
а)  в)
в) 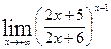
б)  г)
г) 
10.
а)  в)
в) 
б)  г)
г) 
Задачи 21-40
Найти производные функций:
21.
а)  в)
в) 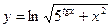
б)  г)
г) 
22.
а)  в)
в) 
б)  г)
г) 
23.
а)  в)
в) 
б)  г)
г) 
24.
а)  в)
в) 
б)  г)
г) 
25.
а)  в)
в) 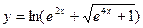
б)  г)
г) 
26.
а)  в)
в) 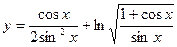
б) 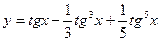 г)
г)


