 |
Расчёт пусковых характеристик
|
|
|
|
ВВЕДЕНИЕ
Асинхронные машины – наиболее распространённые электрические машины. Особенно широко они применяются как электродвигатели, являются основными преобразователями электрической энергии в механическую. Применение асинхронных двигателей в качестве электропривода подавляющего большинства механизмов объясняется простотой конструкции, надёжностью и высоким значением КПД этих машин.
Важнейшим требованием при изготовлении и проектировании двигателей является минимальная материалоёмкость электрических машин. Экономия материалов связана с безотходной и малоотходной технологии. Электрические машины с безотходной технологией изготовления имеют преимущества перед обычными машинами.
Проектируемая электрическая машина должна иметь высокие показатели (КПД и cosφ). Электрические машины с минимальными потерями позволяют уменьшить вложение материалов в энергосистему. Высокие энергетические показатели электрической машины гарантируют снижение уровня текущих затрат на эксплуатацию и капитальные вложения. Вновь разрабатываемые электрические двигатели должны соответствовать, быть надёжными и иметь срок службы 8 – 10 лет.
С 1946 года асинхронные двигатели выпускаются едиными сериями. Это значительно облегчает выбор, установку, обслуживание и ремонт электрооборудования. В 70 – х годах была разработана и внедрена единая серия асинхронных двигателей 4А. Одновременно с конструкцией двигателей разрабатывались электротехническая сталь, провода, изоляция и технология. В 80–х годах организацией социалистических стран «Интерэлектро» разработана новая унифицированная серия асинхронных двигателей АИ, предназначенная для использования во всех странах – членах СЭВ.
|
|
|
1 ОБОСНОВАНИЕ И ВЫБОР ОСНОВНЫХ РАЗМЕРОВ
Данный расчёт производится по методике предложенной в [1].
1.1 Выбираем наружный диаметр статора из ряда рекомендаций близким к наибольшему для получения наименьшей активной длины сердечника машины с целью обеспечения относительно малого активного сопротивления ротора при котором двигатель будет иметь малый пусковой и критический момент [с.344, табл. 9.8].
Для асинхронных двигателей серии 4А при h = 112 мм, Da = 0,195 м.
Рекомендуемые пределы [0,191-0,197] м.
[с.344, табл. 9.8].
1.2 Внутренний диаметр статора [с.344, формула 9.2]:
D = Da · Kd,
где Kd – коэффициент, характеризующий отношения внутренних и внешних диаметров сердечников статоров асинхронных двигателей при различных числах полюсов находится в пределах (0,52 ¸ 0,6), принимаем Kd = 0,55 [с.344, табл. 9.9]:
D = Da · Kd =0,195·0,55 = 0,107 м.
1.3 Полюсное деление τ [с.344, формула 9.3]:

1.4 Расчётная мощность [с.344, формула 9.4]:
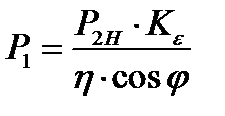 ,
,
где 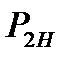 - мощность на валу двигателя, Kε – коэффициент, равный отношению ЭДС обмотки статора к номинальному напряжению, зависит от Da. Выбираем Kε = 0,98 [с.345, рис. 9,20];
- мощность на валу двигателя, Kε – коэффициент, равный отношению ЭДС обмотки статора к номинальному напряжению, зависит от Da. Выбираем Kε = 0,98 [с.345, рис. 9,20];
η - КПД двигателя, зависит от P2н, принимаем равным η = 0,87 о.е;
cosφ – коэффициент мощности, зависит от P2н, принимаем равным cosφ = 0,9 о.е. [с.345, рис. 9,21,а];
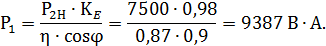
1.5 Предварительный выбор электромагнитных нагрузок. Рекомендуемые пределы А (23×103 ¸ 25×103) А / м, зависит от Da,
принимаем А = 24·103 А / м.
Рекомендуемые пределы Вδ (0.7 ¸ 0.75) Тл, зависит от Da, принимаем
Вδ = 0.74 Тл. [c.346, рис.9,22].
1.6 Обмоточный коэффициент для однослойной обмотки определяем по формуле:
 .
.
1.7 Рассчитаем длину магнитопровода [с.348, формула 9.6]:

,
где kВ – коэффициент формы поля рассчитывается по формуле:
 ;
;
Ω - синхронная угловая частота вала:

1.8 Критерием правильности выбора главных размеров служит отношение λ, определяемое по формуле:
|
|
|
λ = lδ / τ = 0,117 / 0,168 = 0,823.
Полученное значение входит в область рекомендуемых пределов
λ = (0,3-0,9) для 2p=2. Следовательно, главные размеры двигателя  и
и  выбраны верно.
выбраны верно.
2. ЭЛЕКТРОМАГНИТНЫЙ РАСЧЁТ
2.1 Определение числа пазов, количества витков и площади поперечного сечения провода обмотки статора.
2.1.1 Выберем предельные значения зубцового деления tZ1 [с.351, рис. 9.26]:
tZ1min = 0,0123 м; tZ1max = 0,016 м.
2.1.2 Возможное число пазов статора Z1 [с.351, формула 9.16]:


Выбираем окончательно число пазов статора равным Z1 = 24. Выбор обосновывается тем, что число пазов статора в большинстве асинхронных двигателей должно быть кратно числу фаз, а число пазов на полюс и фазу (q) - целым. Обмотки с дробным числом q при сравнительно небольших числах пазов и полюсов, характерных для большинства асинхронных двигателей, приводят к некоторой асимметрии МДС. Большее количество пазов приводит к улучшению рабочих характеристик, но и, одновременно, к увеличению расхода меди, т.е. стоимость машины при этом повышается.
Проверим величину q:
q = Z1 / 2·p·m = 24/ 2·4·3 = 4.
2.1.3 Окончательное значение зубцового деления статора [с.352]:

Рассчитаем номинальный ток обмотки статора [с.352, формула 9.18]:
 А.
А.
Определим число эффективных проводников в пазу. Для этого предварительно, при условии, что число параллельных ветвей обмотки а = 1 рассчитаем [с.352, формула 9.17]:

Принимаем а = 1, тогда значение числа проводников в пазу [с.352, формула 9.19]:

Окончательно принимаем UП = 23.
2.1.4 Число витков в фазе обмотки статора [с.352, формула 9.20]:
 ;
;
2.1.5 Найдём окончательное значение линейной нагрузки [с.353, формула 9.21]:
 А/м,
А/м,
В качестве обмотки выбираем однослойную обмотку из круглого провода.
Рассчитаем значение потока [с.353, формула 9.22]:

Определим значение индукции в воздушном зазоре [с.353, формула 9.23]:
 Тл,
Тл,
Значения А и Вd находятся в допустимых пределах [1,с.346]
При  пределы для А и
пределы для А и  соответственно равны:
соответственно равны:
Для  для
для 
2.1.6 Определим допустимую плотность тока в обмотке статора, с учётом линейной нагрузки двигателя, так как нагрев пазовой части обмотки зависит от произведения линейной нагрузки на плотность тока (AJ) [с.354, формула 9.25]:
 ,
,
где AJ – среднее значение произведения [с.355, рис. 9.27], зависит от Da;
|
|
|
AJ = 142·109 А2/м3
 А /м2..
А /м2..
2.1.7 Площадь поперечного сечения эффективного проводника предварительно [с.353, формула 9.24]:
 м2.
м2.
Полученное значение поперечного сечения эффективного проводника слишком велико и отсутствует в таблице выбора сечений, в обмотках из круглого провода число элементарных проводников может достигать 8-10, поэтому примем число элементарных проводников nэл = 2, тогда
 м2,
м2,
Принимаем обмоточный провод марки ПЭТ-155 [с.713, табл. Приложение 3.1.]:
qэл = 1,227 мм2 – площадь поперечного сечения неизолированного провода;
dиз = 1,33 мм - диаметр изолированного провода;
dэл = 1,25 мм – диаметр неизолированного провода;
Тогда  м2.
м2.
2.1.8 Уточнённое значение плотности тока в обмотке статора [с.356, формула 9.27]:
 А /м2.
А /м2.
Данное значение удовлетворяет допустимым пределам для двигателя мощностью 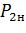 =7,5 кВт, которые составляют [5,5-7,5] А /м2. Отклонение уточненного значения плотности тока от предварительного составляет ≤ 5%, следовательно расчет выполнен верно.
=7,5 кВт, которые составляют [5,5-7,5] А /м2. Отклонение уточненного значения плотности тока от предварительного составляет ≤ 5%, следовательно расчет выполнен верно.
На этом расчет обмотки статора заканчивается. Некоторая корректировка, которая может потребоваться в ходе последующего расчета, как правило, не вносит существенных изменений в полученные данные.
2.2 Расчёт зубцовой зоны статора и воздушного зазора.
2.2.1 Выбор формы паза статора.
Круглые обмоточные провода всыпной обмотки могут быть уложены в пазы произвольной конфигурации, поэтому размеры зубцовой зоны при всыпных обмотках выбирают таким образом, чтобы параллельные грани имели зубцы, а не пазы статора. Такие зубцы имеют постоянное, не изменяющееся с высотой зубца поперечное сечение, индукция в них также не изменяется, и магнитное напряжение зубцов с параллельными гранями оказывается меньше, чем магнитное напряжение трапецеидальных зубцов, при том же среднем значении индукции в них. Это объясняется отсутствием в зубцах с параллельными гранями участков с высокой индукцией, напряжённость поля в которых резко возрастает из-за нелинейности магнитной характеристики стали, увеличивая суммарное магнитное напряжение зубцов. В большинстве современных двигателей выполняют трапецеидальные пазы. Поэтому выбираем именно такие пазы (Рисунок 1).
|
|
|
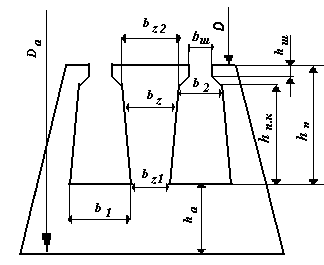
Рисунок 1 – Вид пазов статора
2.2.2 Расчёт зубцовой зоны статора.
Выбираем допустимые значения индукции [с.357, табл. 9.12]:
ярма статора – Ва = 1,45 Тл; рекомендуемые пределы (1,4 ¸ 1,6) Тл,
зубцов статора при постоянном сечении – ВZ1 = 1,8 Тл, рекомендуемые пределы (1,6 ¸ 1,9) Тл.
Выбираем способ изолирования листов – оксидирование, тогда коэффициент заполнения сердечника сталью kc = 0,97 [ с.358, табл. 9.13].
2.2.3 Определим ширину зубцов статора [с.358, формула 9.29]:
 .
.
Найдём высоту ярма статора [с.356, формула 9.28]:
 м.
м.
Высота шлица hш =0,5·10-3 м, для двигателей с h = 100 мм. Высота шлица полузакрытых пазов bш =3.5·10-3 м [с.360].
Определим размеры паза в штампе [с.178, формулы 9.31, 9.40, 6-41]:
Высота паза:
 м;
м;


Клиновую часть паза найдём из выражения [с.365, формулы 9.44]:
 м,
м,
Где 
2.2.4 Размеры паза в свету с учётом припуска на шихтовку сердечника [с.360]:
Δb = 0,1·10-3 м; Δh = 0,1·10-3 м;
 м,
м,

 м,
м,
Одностороннюю толщину изоляции в пазу принимаем: b из = 0,25·10-3 м.
Площадь поперечного сечения корпусной изоляции в пазу [c.365, формула 9.46]:
 м2,
м2,
Площадь поперечного сечения паза для размещения проводников обмотки [с.365, формула 9.48]:
 м2.
м2.
2.2.5 Подсчитаем коэффициент заполнения паза, который является контролем правильности размещения обмотки в пазах [с.366]:
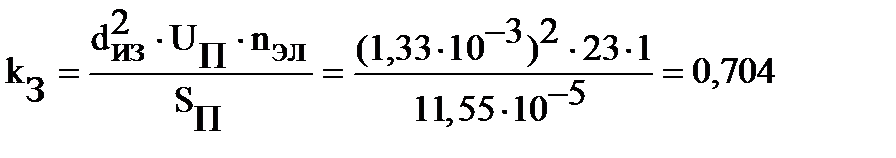
Полученное значение kз допустимо для механизированной укладки обмотки (kз= 0,69- 0,71 при 2р=2).
Затем уточняем ширину зубца и высоту паза по формулам таблицы 9.17. [с.366]:
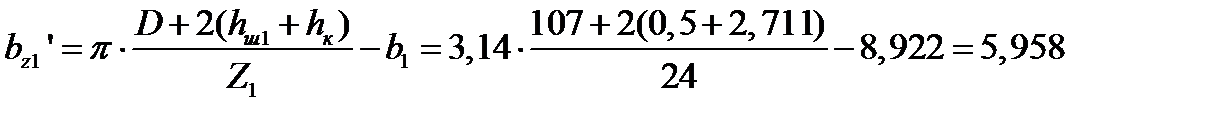 мм,
мм,
 мм,
мм,
 мм.
мм.
Проверяем параллельность граней зубца по выражению
 .
.
Расчёт ротора
2.3.1 Воздушный зазор [с.367, рис. 9.31], зависит от D: δ = 0.4·10-3 м.
Правильный выбор воздушного зазора δ во многом определяет энергетические показатели асинхронного двигателя. Чем меньше воздушный зазор, тем меньше его магнитное сопротивление и магнитное напряжение, составляющее основную часть МДС магнитной цепи всей машины. Поэтому уменьшение зазора приводит к соответственному уменьшению МДС магнитной цепи и намагничивающего тока двигателя, благодаря чему возрастает его cosφ и уменьшаются потери в меди обмотки статора. Но чрезмерное уменьшение δ приводит к возрастанию амплитуды пульсаций индукции в воздушном зазоре и, как следствие этого, к увеличению поверхностных и пульсационных потерь. Поэтому КПД двигателей с очень малыми зазорами не улучшается, а часто даже становится меньше. Необходимо также учесть условие механической прочности так, чтобы прогиб вала не привёл к касанию сердечников ротора и статора.
2.3.2 Число пазов ротора [с.373, табл. 9.18], зависит от 2р: Z2 = 19.
|
|
|
Выбор пазов ротора особо важен, так как в поле воздушного зазора машины кроме основной присутствует целый спектр гармоник более высокого порядка, каждая из которых наводит ЭДС в обмотке ротора, поэтому ток в стержнях обмотки имеет сложный гармонический состав. В зависимости от соотношения Z1 и Z2 в той или иной степени проявляются синхронные или асинхронные моменты от высших гармоник. Их влияние на момент от первой гармонической приводит к появлению пиков и провалов в результирующей кривой момента. В поле зазора присутствуют также высшие гармоники, порядок которых определенным образом связан с числами пазов и полюсов машины. Эти зубцовые гармоники вызывают шум и вибрацию при работе двигателя в номинальном режиме. Их влияние особо заметно при малых воздушных зазорах. В двигателях малой мощности обычно выполняют Z1 > Z2. Это связано с технологией изготовления, а также тем, что с увеличением Z2 ток в стержнях ротора уменьшается и в двигателях небольшой мощности их сечения становятся очень малыми.
2.3.4 Внешний диаметр ротора:
 м.
м.
2.3.5 Длинна магнитопровода ротора:
l2 = ld = 0,139 м.
2.3.6 Зубцовое деление ротора:
 м.
м.
2.3.7 Внутренний диаметр ротора равен диаметру вала, так как сердечник ротора непосредственно насаживается на вал [с.385, формула 9.102]:

где kB = 0.23 - эмпирический коэффициент [с.385, табл. 9.19], зависит от h и 2р.
2.3.8 Ток в стержне ротора [с.370, формула 9.57]:
 ,
,
где ki - коэффициент, учитывающий влияние тока намагничивания на отношение I1 / I2:

vi - коэффициент приведения токов [с.185, формула 6-68]:
 ,
,
 А.
А.
2.3.9 Площадь поперечного сечения стержня предварительно [с.186, формула 6-69]:
 ,
,
где J2 = 3,5 ·106 А /м2 – плотность тока в стержнях ротора машин закрытого обдуваемого исполнения при заливке пазов алюминием;
Тогда:


2.3.10 Выбираем пазы ротора грушевидной формы. (см. Рисунок 2)
Форма паза и конструкция обмотки короткозамкнутого ротора определяются требованиями к пусковым характеристикам двигателя и его мощностью. В асинхронных двигателях мощностью до 50 – 60 кВт обычно выполняют грушевидные пазы и литую обмотку из алюминия.
Размеры шлица [с.380]: b ш2 = 0,75·10-3 м, hш2 =1,5·10-3 м,
Выбираем допустимую индукцию для зубцов ротора [с.380, табл. 9.12]
ВZ 2 = 1,8Тл, рекомендуемые пределы (1,6 ¸ 1,9) Тл,
Допустимая ширина зубца [с.380, формула 9.75]:
 м,
м,
Размеры паза [с.380, формулы 9.76, 9.77, 9.78]:
 м,
м, 
 м.
м.

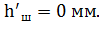
2.3.11 Площадь поперечного сечения стержня [с.380, формула 9.79]  ,
,
2.3.12 Полная высота паза:

2.3.13 Плотность тока в стержне:
 А /м2.
А /м2.
2.3.14 Необходимо проверить ширину зубцов сердечника ротора:
 мм,
мм,
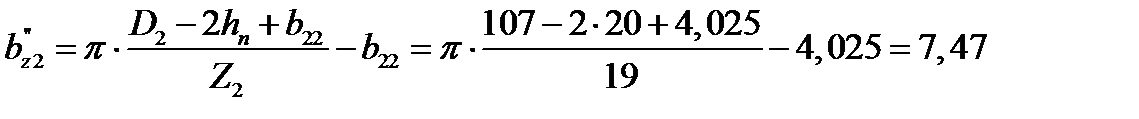 м.
м.
Проверяем параллельность граней зубца
 мм,
мм,
условие выполняется.
 мм.
мм.
2.3.15 Короткозамыкающие кольца:
Ток в короткозамкнутом кольце [с.376, формула 9.70]:
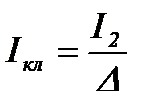 ,
,
где Δ – коэффициент [с.376, формула 9.71]:
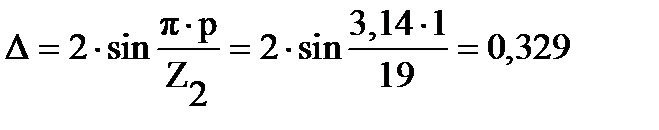
тогда:
 A,
A,

Рисунок 2 – Грушевидные пазы ротора
Плотность тока в замыкающих кольцах выбирают в среднем на 15 – 20% меньше, чем в стержнях из-за лучших условий охлаждения колец, а также потому, что в машинах, в которых для улучшения пусковых характеристик используют эффект вытеснения тока, большое сопротивление замыкающих колец снижает кратность увеличения общего сопротивления обмотки ротора при пуске.
 A / м2,
A / м2,
Площадь поперечного сечения кольца [с.376, формула 9.72]:
 м2,
м2,
Размеры замыкающих колец:
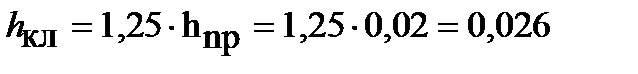 м,
м,
 м,
м,
 .
.

Рисунок 3 – Размеры замыкающих колец короткозамкнутого ротора
Расчёт магнитной цепи
Выбираем магнитопровод из стали 2013; толщина листов 0,5 мм.
Марку электротехнической стали рекомендуется выбирать в зависимости от высоты оси вращения проектируемого асинхронного двигателя. Для высоты оси вращения 45…250мм выбираем сталь 2013.
2.4.1
Магнитное напряжение воздушного зазора [c.386, формула 9.103]:
 ,
,
где kδ – коэффициент воздушного зазора [c.173, формула 4.15]:
 ,
,
m0 – магнитная постоянная, m0 = 4p×10-7 Гн/м; где  ,
,
тогда:
 ,
,
тогда:
2.4.2  А.
А.
2.4.3 Для определения магнитного напряжения зубцовой зоны статора прежде найдём индукцию в них[c.387, формула 9.105]:
 Тл,
Тл,
Магнитное напряжение зубцовой зоны статора [с.387, формула 9.104]:

hZ 1 - высота зубца, hZ1 = hП = 0,016 м;
HZ1 – напряжение зубцовой зоны статора [c.698 табл. Приложение 1.7]
HZ1 = 1520 А /м, для ВZ1 = 1,8 Тл.
тогда:
 А.
А.
2.4.3 Для определения магнитного напряжения зубцовой зоны ротора прежде найдём индукцию в них[с.390, формула 9.109]:
 Тл,
Тл,
Магнитное напряжение зубцовой зоны ротора [с.388, формула 9.108]:
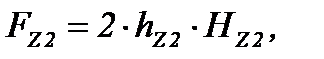
hZ 2 - высота зубца hZ2 =0,02-0,1*8,9∙10-3 =0,02 м,
HZ2 – напряжение зубцовой зоны ротора [с.696, табл. Приложение 1.5]
HZ2 = 1520 А /м, для ВZ2 = 1,8 Тл.
тогда:
 А.
А.
2.4.4 Коэффициент насыщения зубцовой зоны [с.391, формула 9.115]:
 ,
,
Если kZ > 1,6, имеет место чрезмерное насыщение зубцовой зоны; если kZ < 1,2то зубцовая зона мало использована или воздушный зазор взят слишком большим. В данном расчёте коэффициент насыщения зубцовой зоны входит в диапазон рекомендуемых значений.
2.4.5 Магнитное напряжение ярма статора. Предварительно найдём длину средней магнитной силовой линии в ярме [c.394, формула 9.119]:
 м,
м,
Индукция в ярме статора [c.394, формула 9.117]:
 Тл,
Тл,
Напряжённость поля ярма статора при индукции [c.697 табл. Приложение 1,6] Ва = 1,45 Тл, Ha = 450 A/м,
тогда магнитное напряжение:
 А.
А.
Магнитное напряжение ярма ротора. Рассчитаем длину ярма ротора [c.395, формула 9.126]:
 м,
м,
Предварительно определим длину средней магнитной силовой линии в ярме ротора [c.395, формула 9.127]:
 м,
м,
В двигателях с непосредственной посадкой сердечника ротора на вал часть силовых магнитных линий замыкаются через вал, поэтому расчетную высоту ярма ротора, м, определяют [c.395]:
 ,
,
Индукция в ярме ротора [c.395, формула 9.122]:
 Тл,
Тл,
Напряжённость поля ярма ротора при индукции Вj = 1,33 Тл [c.697 табл. П 1.6]
Hj = 341 A /м, тогда магнитное напряжение:
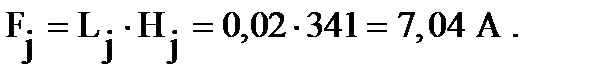
2.4.6 Магнитное напряжение на пару полюсов [c.396, формула 9.128]:
 А.
А.
2.4.7 Коэффициент насыщения магнитной цепи [c.9.129, формула 9.129]:
 ,
,
Данное значение попадает в допустимые пределы  = [1,1-1,3].
= [1,1-1,3].
Намагничивающий ток [c.396, формула 9.130]:
 А,
А,
Выразим намагничивающий ток в долях номинального тока двигателя
[c.396, формула 9.131]: 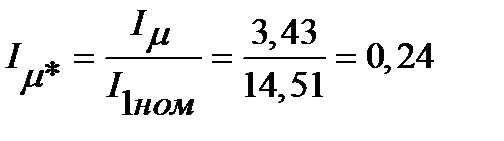 ,
,
Относительное значение Im* служит определенным критерием правильности произведенного выбора и расчета размеров и обмотки двигателя. Так, если при Im* < 0,20 ¸ 0,18, то это свидетельствует о том, что размеры машины выбраны завышенными и активные материалы недоиспользованы. Такой двигатель может иметь высокие КПД и cosj, но плохие показатели расхода материалов на единицу мощности, большую массу и габариты.
Если же в аналогичном двигателе Im* > 0,30 ¸ 0,35, то это означает, что либо его габариты взяты меньшими, чем следовало, либо неправильно выбраны размерные соотношения участков магнитопровода. Двигатель будет иметь низкие КПД и cosj.
В нашем случае значение Im* вошло в рекомендуемые пределы  , это значит что размеры машины выбраны рационально.
, это значит что размеры машины выбраны рационально.
Параметры рабочего режима
Параметрами асинхронной машины называют активные и индуктивные сопротивления обмоток статора r1, x1, ротора или приведенные к числу витков обмотки статора сопротивления ротора r2’, x2’, сопротивление взаимной индуктивности x12 и расчетное сопротивление r12, введением которого учитывают влияние потерь в стали статора на характеристики двигателя.

Рисунок – 4. Схемы замещения фаз обмотки асинхронной машины
2.5.2 Определим среднюю ширину катушки [c.399, формула 9.138]:
 м,
м,
Длинна вылета лобовой части катушки [c.398, формула 9.137]:
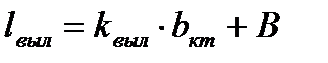 ,
,
где kвыл - коэффициент, зависит от числа полюсов [c.399, таблица 9.23], для не изолированных лентой лобовых частей примем при 2р = 2, kвыл = 0,26;
В – длина вылета прямолинейной части катушек из паза [с. 399]: В = 0,01 – для всыпной обмотки,
тогда:
 м,
м,
Длинна пазовой части равна конструктивной длине сердечников машины:
lП = lδ = 0,139 м,
Длинна лобовой части всыпной обмотки [с.398, формула 9.136]:
 ,
,
где kл - коэффициент, зависит от числа полюсов [с.399, табл. 9.23], для изолированных лентой лобовых частей kл = 1,4
 м,
м,
Средняя длинна витка [с.398, формула 9.135]:
 м,
м,
Общая длинна проводников фазы обмотки [с.398, формула 9.134]:
 м,
м,
2.5.3 Активное сопротивление обмотки статора [с.397, формула 9.132]:
 Ом,
Ом,
где ρ115 = 10-6 / 41 Ом ·м - удельное сопротивление меди при температуре плюс 115 0С; коэффициент увеличения активного сопротивления фазы обмотки от действия эффекта вытеснения тока, kR = 1, так как в проводниках обмотки статора асинхронных машин эффект вытеснения тока проявляется незначительно из-за малых размеров элементарных проводников [с. 398].
Относительное значение активного сопротивления обмотки статора [c.411]:
 Ом,
Ом,
Относительные значения активного сопротивления обмотки статора находятся в пределах
 , [1,с.411]. По учебному пособию «Асинхронные двигатели серии 4А: справочник» / А. Э. Кравчик и др., М: Энергоатомиздат, 1982 – 504 с.,[2,с.53] после выбора аналога, а именно, для нашей машины, двигатель 4А112L2У3, его значение
, [1,с.411]. По учебному пособию «Асинхронные двигатели серии 4А: справочник» / А. Э. Кравчик и др., М: Энергоатомиздат, 1982 – 504 с.,[2,с.53] после выбора аналога, а именно, для нашей машины, двигатель 4А112L2У3, его значение  . Так как расхождение с аналогом не превышает 5%, то при дальнейшем расчете будем сравнивать полученные значения с этим двигателем.
. Так как расхождение с аналогом не превышает 5%, то при дальнейшем расчете будем сравнивать полученные значения с этим двигателем.
2.5.4 Сопротивление стержня обмотки ротора [с.406, формула 9.169]:
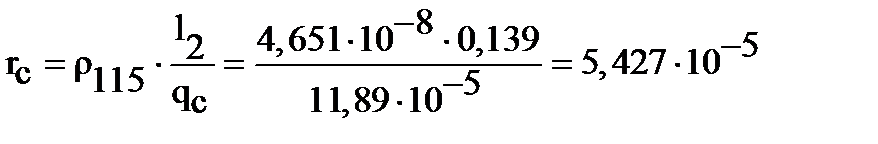 Ом,
Ом,
где ρ115 = 10-6 / 21,5 Ом ·м - удельное сопротивление литой алюминиевой обмотки ротора при температуре плюс 115 0С, класс изоляции F.
Сопротивление участка замыкающего кольца, заключённого между двумя соседними стержнями [с.406, формула 9.170]:
 Ом,
Ом,
2.5.5 Активное сопротивление фазы обмотки ротора [с.406, формула 9.168]:
 Ом,
Ом,
Для дальнейших расчётов полученное сопротивление фазы обмотки ротора к числу витков обмотки статора [с.406, формулы 9.172, 9.173]:
 Ом,
Ом,
Относительное значение [c.411]:
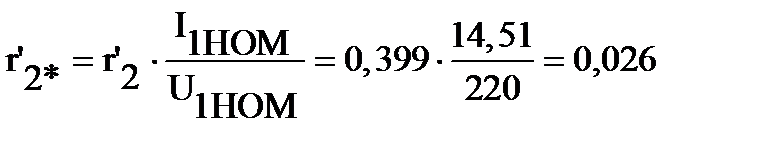 .
.
Данное значение входит в требуемые пределы  . Можно с уверенностью утверждать, что расчет произведен правильно.
. Можно с уверенностью утверждать, что расчет произведен правильно.
2.5.6 Коэффициенты магнитной проводимости.
Коэффициент магнитной проводимости пазового рассеяния [с.403, табл. 9.26]:
 ,
,
Проводники закрыты пазовой крышкой;
 ,
,
 .
.
Коэффициент магнитной проводимости лобового рассеяния [c.403, формула 9.159]:
 ,
,
Коэффициент магнитной проводимости дифференциального рассеяния
[c.403, формула 9.160]:
 ,
,
где ξ – коэффициент, зависящий от числа q, укорочения шага обмотки и размерных соотношений зубцовых зон и воздушного зазора. [c.404, формула 9.161]:
 ,
,
пазы без скоса βск = 0, k’ск = 1,35,[c.405, рис. 9.51],зависит от tz1/tz2
тогда:
 ,
,
2.5.7 Индуктивное сопротивление фазы обмотки статора [c.407, формула 9.174]:
 , Ом.
, Ом.
Относительное значение индуктивного сопротивления фазы обмотки статора [c.205]:
 .
.
Относительные значения одних и тех же параметров схемы замещения различных асинхронных двигателей незначительно отличаются друг от друга. Относительные значения индуктивного сопротивления обмотки ротора находятся в пределах 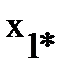 =0,08-…-0,14, [1,с.411]. Следовательно, полученное значение входит в рекомендуемые пределы.
=0,08-…-0,14, [1,с.411]. Следовательно, полученное значение входит в рекомендуемые пределы.
2.5.8 Коэффициент магнитной проводимости пазового рассеяния ротора
[c.408, табл. 9.27]:
 ,
,
Где 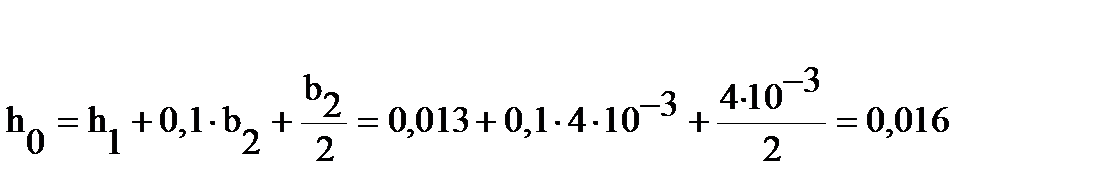 м,
м,
 ,
,
Коэффициент магнитной проводимости лобового рассеяния [c.409, формула 9.178]:
 ,
,
 ,
,
Коэффициент магнитной проводимости дифференциального рассеяния обмотки, короткозамкнутого ротора [c.409, формула 9.180]:
 ,
,
где ξ – коэффициент, зависящий от числа q, укорочения шага обмотки и размерных соотношений зубцовых зон и воздушного зазора. [c.409, формула 9.181]:
 ,
,
ΔZ =0,02.

2.5.9 Индуктивное сопротивление фазы обмотки статора [c.407, формула 9.177]:
 Приводим X2 к числу витков статора [c.409, формула 9.183]:
Приводим X2 к числу витков статора [c.409, формула 9.183]:
 Ом,
Ом,
Относительное значение[c.411]:
 .
.
Для удобства сопоставления параметров отдельных машин и упрощения расчёта характеристик параметры асинхронных машин выражают в относительных единицах, принимая за базисные значения номинальное фазное напряжение и номинальный фазный ток.
Относительные значения одних и тех же параметров схемы замещения различных асинхронных двигателей незначительно отличаются друг от друга. Относительные значения индуктивного сопротивления обмотки статора находятся в пределах  . Следовательно, полученное значение входит в рекомендуемые пределы.
. Следовательно, полученное значение входит в рекомендуемые пределы.
Расчёт потерь
2.6.1 Основные потери в стали статора асинхронной машины [c.412, формула 9.187]:
 ,
,
где p0 / 50 - удельные потери при индукции 1 Тл и частоте перемагничивания 50 Гц [c.412, табл. 9.28]: p0 / 50 = 2.5 Вт / кг;
β – показатель степени, учитывающий зависимость потерь в стали от частоты перемагничивания, для большинства сталей β =1,3… 1.5; β =1.5
kда и kдz – коэффициенты, учитывающие влияние на потери в стали неравномерности распределения потока по сечениям участков магнитопровода и технологических факторов kда = 1,6, kдz = 1,8, та, mZ1 - масса стали ярма и зубцов статора [c.412, формулы 9.188, 9.189]:
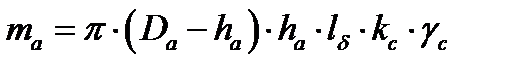 ,
,
 ,
,
где γс – удельная масса стали; в расчётах принимают γс = 7,8·103 кг / м3 [с.349 ],
 , кг,
, кг,
 кг,
кг,
тогда:
 Вт.
Вт.
2.6.2. Добавочные потери в стали (добавочные потери холостого хода) подразделяются на поверхностные (потери в поверхностном слое кромок зубцов статора и ротора от пульсаций индукции в воздушном зазоре) и пульсационные потери в стали зубцов (от пульсации индукции в зубцах).
Для нахождения поверхностных потерь прежде находят амплитуду пульсаций индукции в воздушном зазоре над коронками зубцов ротора [c.413, формула 9.190]:
 ,
,
где β02 = (bш / δ)=7,8; β02 =0.38 [с.413, рисунок 9.53],
Поверхностные потери в роторе [с.413, формула 9.193]:
 ,
,
где pпов2 - удельные поверхностные потери, т.е. потери, в поверхностном слое коронок зубцов ротора [с.413, формула 9.192]:
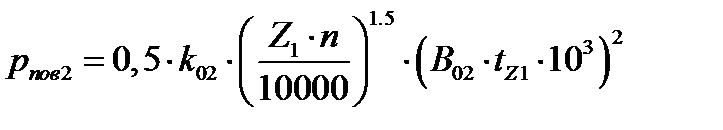 ,
,
где k02 - коэффициент, учитывающий влияние обработки поверхности головок зубцов ротора на удельные потери[с.413], k02 =1,4;
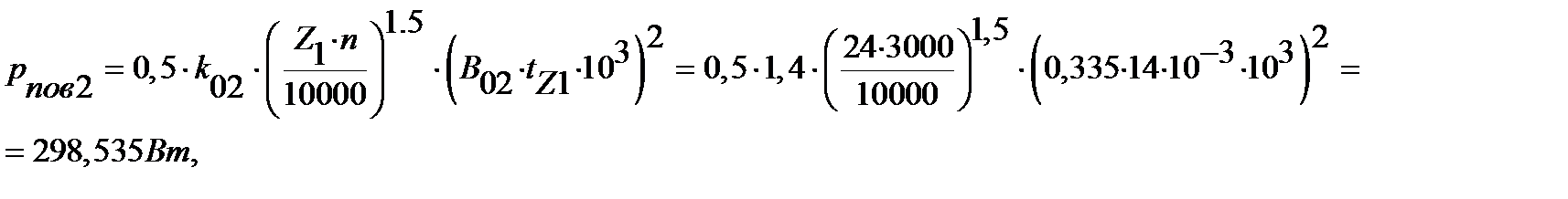 тогда:
тогда:
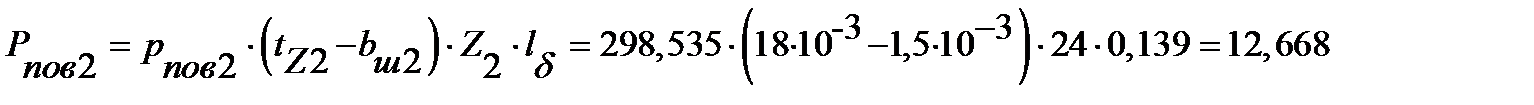 Вт.
Вт.
2.6.3 Для определения пульсационных потерь необходимо определить массу ротора [с.414, формула 9.201]:
 кг,
кг,
а также амплитуду пульсаций индукции в среднем сечении зубцов [с.413, формула 9.196]:
 Тл,
Тл,
тогда пульсационные потери в зубцах ротора [с.414, формула 9.200]:
 Вт.
Вт.
2.6.4 Сумма добавочных потерь в стали [с.415, формула 9.202]:
 Вт.
Вт.
2.6.5 Полные потери в стали [с.415, формула 9.203]:
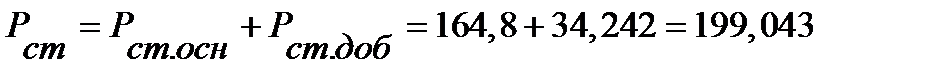 Вт.
Вт.
2.6.6 Механические потери [с.416, формула 9.210]:
 Вт,
Вт,
где KТ - коэффициент трения, учитывающий конструкцию, скорость вращения, число пар полюсов, мощность двигателя; для двигателей с2·p = 2равен KТ =1,0465 [с. 416]Добавочные потери при номинальном режиме [с.417]:
 Вт.
Вт.
2.6.7 Для определения тока холостого хода двигателя принимают, что потери на трение и вентиляцию и потери в стали при холостом ходе такие же, как и при номинальном режиме. При этом условии активная составляющая тока холостого хода: [с.417, формула 9.218]:
 ,
,
где Pэ1.х.х – электрические потери в статоре при холостом ходе [с.417, формула 9.219]:

 Вт,
Вт,
тогд
|
|
|


