Равнобедренный теругольник

58. Сто­ро­на рав­но­сто­рон­не­го тре­уголь­ни­ка равна 10. Най­ди­те его пло­щадь, делённую на .

59. Пе­ри­метр рав­но­сто­рон­не­го тре­уголь­ни­ка равен 30. Най­ди­те его пло­щадь, делённую на .

60. Вы­со­та рав­но­сто­рон­не­го тре­уголь­ни­ка равна 10. Най­ди­те его пло­щадь, делённую на

61. Пе­ри­метр рав­но­бед­рен­но­го тре­уголь­ни­ка равен 16, а бо­ко­вая сто­ро­на — 5. Най­ди­те пло­щадь тре­уголь­ни­ка.

62. Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

63. Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

 

.

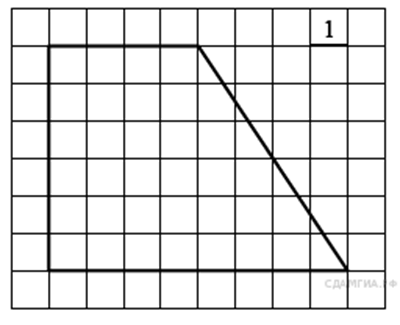
64. Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

 

65. Ос­но­ва­ния тра­пе­ции равны 18 и 12, одна из бо­ко­вых сто­рон равна , а угол между ней и одним из ос­но­ва­ний равен 135°. Най­ди­те пло­щадь тра­пе­ции.

66. Ос­но­ва­ния тра­пе­ции равны 18 и 12, одна из бо­ко­вых сто­рон равна 6, а синус угла между ней и одним из ос­но­ва­ний равен . Най­ди­те пло­щадь тра­пе­ции.

Параллеллограмм

 

67. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ражённого на ри­сун­ке.

68. Сто­ро­на ромба равна 5, а диа­го­наль равна 6. Най­ди­те пло­щадь ромба.

69. Пе­ри­метр ромба равен 40, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

70. Пе­ри­метр ромба равен 24, а синус од­но­го из углов равен 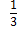. Най­ди­те пло­щадь ромба.

71. Одна из сто­рон па­рал­ле­ло­грам­ма равна 12, а опу­щен­ная на нее вы­со­та равна 10. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма.

Треугольники об­ще­го вида

72. В тре­уголь­ни­ке одна из сто­рон равна 10, а опу­щен­ная на нее вы­со­та — 5. Най­ди­те пло­щадь тре­уголь­ни­ка.

73. В тре­уголь­ни­ке одна из сто­рон равна 10, дру­гая равна , а угол между ними равен 60°. Най­ди­те пло­щадь тре­уголь­ни­ка.

Фигуры на квад­рат­ной решётке

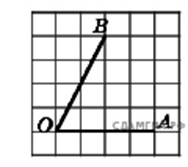
74. Най­ди­те тан­генс угла AOB, изоб­ра­жен­но­го на ри­сун­ке.

75. Най­ди­те тан­генс угла А тре­уголь­ни­ка ABC, изоб­ражённого на ри­сун­ке.

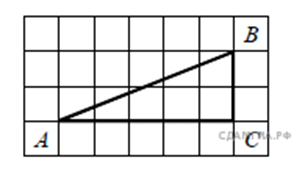
76. Най­ди­те тан­генс угла B тре­уголь­ни­ка ABC, изоб­ражённого на ри­сун­ке.

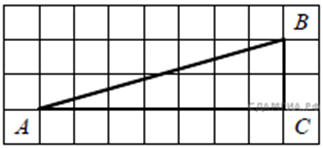
77. Най­ди­те тан­генс угла С тре­уголь­ни­ка ABC, изоб­ражённого на ри­сун­ке.

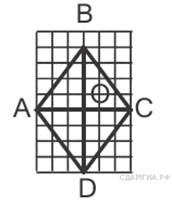
78. На ри­сун­ке изоб­ра­же­на тра­пе­ция . Ис­поль­зуя ри­су­нок, най­ди­те .

79. На ри­сун­ке изоб­ра­жен ромб . Ис­поль­зуя ри­су­нок, най­ди­те .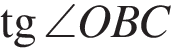

 

Анализ гео­мет­ри­че­ских высказываний

80. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

 

1) Если два угла од­но­го тре­уголь­ни­ка равны двум углам дру­го­го тре­уголь­ни­ка, то такие тре­уголь­ни­ки по­доб­ны.

2) Вер­ти­каль­ные углы равны.

3) Любая бис­сек­три­са рав­но­бед­рен­но­го тре­уголь­ни­ка яв­ля­ет­ся его ме­ди­а­ной.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

81. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

 

1) Су­ще­ству­ет квад­рат, ко­то­рый не яв­ля­ет­ся пря­мо­уголь­ни­ком.

2) Если два угла тре­уголь­ни­ка равны, то равны и про­ти­во­ле­жа­щие им сто­ро­ны.

3) Внут­рен­ние на­крест ле­жа­щие углы, об­ра­зо­ван­ные двумя па­рал­лель­ны­ми пря­мы­ми и се­ку­щей, равны.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

82. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

 

1) Бис­сек­три­са рав­но­бед­рен­но­го тре­уголь­ни­ка, про­ведённая из вер­ши­ны, про­ти­во­ле­жа­щей ос­но­ва­нию, делит ос­но­ва­ние на две рав­ные части.

2) В любом пря­мо­уголь­ни­ке диа­го­на­ли вза­им­но пер­пен­ди­ку­ляр­ны.

3) Для точки, ле­жа­щей на окруж­но­сти, рас­сто­я­ние до цен­тра окруж­но­сти равно ра­ди­у­су.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

83. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

 

1) Цен­тры впи­сан­ной и опи­сан­ной окруж­но­стей рав­но­сто­рон­не­го тре­уголь­ни­ка сов­па­да­ют.

2) Су­ще­ству­ет квад­рат, ко­то­рый не яв­ля­ет­ся ром­бом.

3) Сумма углов лю­бо­го тре­уголь­ни­ка равна 180°.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

84. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

 

1) Если угол ост­рый, то смеж­ный с ним угол также яв­ля­ет­ся ост­рым.

2) Диа­го­на­ли квад­ра­та вза­им­но пер­пен­ди­ку­ляр­ны.

3) В плос­ко­сти все точки, рав­но­удалённые от за­дан­ной точки, лежат на одной окруж­но­сти.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

85. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

 

1) Если три сто­ро­ны од­но­го тре­уголь­ни­ка про­пор­ци­о­наль­ны трём сто­ро­нам дру­го­го тре­уголь­ни­ка, то тре­уголь­ни­ки по­доб­ны.

2) Сумма смеж­ных углов равна 180°.

3) Любая вы­со­та рав­но­бед­рен­но­го тре­уголь­ни­ка яв­ля­ет­ся его бис­сек­три­сой.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

86. Какие из сле­ду­ю­щих утвер­жде­ний верны?

 

1) Если угол равен 45°, то вер­ти­каль­ный с ним угол равен 45°.

2) Любые две пря­мые имеют ровно одну общую точку.

3) Через любые три точки про­хо­дит ровно одна пря­мая.

4) Если рас­сто­я­ние от точки до пря­мой мень­ше 1, то и длина любой на­клон­ной, про­ве­ден­ной из дан­ной точки к пря­мой, мень­ше 1.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

87. Какие из сле­ду­ю­щих утвер­жде­ний верны?

 

1) Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой со­от­вет­ствен­ные углы равны 65°, то эти две пря­мые па­рал­лель­ны.

2) Любые две пря­мые имеют не менее одной общей точки.

3) Через любую точку про­хо­дит более одной пря­мой.

4) Любые три пря­мые имеют не менее одной общей точки.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

88. Какие из сле­ду­ю­щих утвер­жде­ний верны?

 

1) Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой внут­рен­ние на­крест ле­жа­щие углы со­став­ля­ют в сумме 90°, то эти две пря­мые па­рал­лель­ны.

2) Если угол равен 60°, то смеж­ный с ним равен 120°.

3) Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой внут­рен­ние од­но­сто­рон­ние углы равны 70° и 110°, то эти две пря­мые па­рал­лель­ны.

4) Через любые три точки про­хо­дит не более одной пря­мой.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

89. Какие из сле­ду­ю­щих утвер­жде­ний верны?

 

1) Впи­сан­ные углы, опи­ра­ю­щи­е­ся на одну и ту же хорду окруж­но­сти, равны.

2) Если ра­ди­у­сы двух окруж­но­стей равны 5 и 7, а рас­сто­я­ние между их цен­тра­ми равно 3, то эти окруж­но­сти не имеют общих точек.

3) Если ра­ди­ус окруж­но­сти равен 3, а рас­сто­я­ние от цен­тра окруж­но­сти до пря­мой равно 2, то эти пря­мая и окруж­ность пе­ре­се­ка­ют­ся.

4) Если впи­сан­ный угол равен 30°, то дуга окруж­но­сти, на ко­то­рую опи­ра­ет­ся этот угол, равна 60°.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

90. Какие из сле­ду­ю­щих утвер­жде­ний верны?

 

1) Через любые три точки про­хо­дит не более одной окруж­но­сти.

2) Если рас­сто­я­ние между цен­тра­ми двух окруж­но­стей боль­ше суммы их диа­мет­ров, то эти окруж­но­сти не имеют общих точек.

3) Если ра­ди­у­сы двух окруж­но­стей равны 3 и 5, а рас­сто­я­ние между их цен­тра­ми равно 1, то эти окруж­но­сти пе­ре­се­ка­ют­ся.

4) Если дуга окруж­но­сти со­став­ля­ет 80°, то впи­сан­ный угол, опи­ра­ю­щий­ся на эту дугу окруж­но­сти, равен 40°.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

91. Какие из сле­ду­ю­щих утвер­жде­ний верны?

 

1) Сумма углов вы­пук­ло­го че­ты­рех­уголь­ни­ка равна 180°.

2) Если один из углов па­рал­ле­ло­грам­ма равен 60°, то про­ти­во­по­лож­ный ему угол равен 120°.

3) Диа­го­на­ли квад­ра­та делят его углы по­по­лам.

4) Если в че­ты­рех­уголь­ни­ке две про­ти­во­по­лож­ные сто­ро­ны равны, то этот че­ты­рех­уголь­ник — па­рал­ле­ло­грамм.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

92. Какие из сле­ду­ю­щих утвер­жде­ний верны?

 

1) Если в па­рал­ле­ло­грам­ме диа­го­на­ли равны, то этот па­рал­ле­ло­грамм — пря­мо­уголь­ник.

2) Если диа­го­на­ли па­рал­ле­ло­грам­ма делят его углы по­по­лам, то этот па­рал­ле­ло­грамм — ромб.

3) Если один из углов, при­ле­жа­щих к сто­ро­не па­рал­ле­ло­грам­ма, равен 50°, то дру­гой угол, при­ле­жа­щий к той же сто­ро­не, равен 50°.

4) Если сумма трех углов вы­пук­ло­го че­ты­рех­уголь­ни­ка равна 200°, то его чет­вер­тый угол равен 160°.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

93. Какие из сле­ду­ю­щих утвер­жде­ний верны?

 

1) Около вся­ко­го тре­уголь­ни­ка можно опи­сать не более одной окруж­но­сти.

2) В любой тре­уголь­ник можно впи­сать не менее одной окруж­но­сти.

3) Цен­тром окруж­но­сти, опи­сан­ной около тре­уголь­ни­ка, яв­ля­ет­ся точка пе­ре­се­че­ния бис­сек­трис.

4) Цен­тром окруж­но­сти, впи­сан­ной в тре­уголь­ник, яв­ля­ет­ся точка пе­ре­се­че­ния се­ре­дин­ных пер­пен­ди­ку­ля­ров к его сто­ро­нам.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

 

Задачи с практическим содержание

94. Лест­ни­цу дли­ной 3 м при­сло­ни­ли к де­ре­ву. На какой вы­со­те (в мет­рах) на­хо­дит­ся верх­ний её конец, если ниж­ний конец от­сто­ит от ство­ла де­ре­ва на 1,8 м?

95. Точка крепл ния троса, удерживающего флагшток в вертикальном положении,

находится на высоте 4,4 м от земли. Расстояние от основания флагштока до

места крепления троса на земле равно 3,3 м. Найдите длину троса в метрах.

96. Ко­рот­кое плечо шлаг­бау­ма имеет длину 1 м, а длин­ное плечо – 4 м. На какую вы­со­ту (в мет­рах) под­ни­ма­ет­ся конец длин­но­го плеча, когда конец ко­рот­ко­го опус­ка­ет­ся на 0,5 м?

97. Про­ек­тор пол­но­стью осве­ща­ет экран A вы­со­той 80 см, рас­по­ло­жен­ный на рас­сто­я­нии 250 см от про­ек­то­ра. На каком наи­мень­шем рас­сто­я­нии (в сан­ти­мет­рах) от про­ек­то­ра нужно рас­по­ло­жить экран B вы­со­той 160 см, чтобы он был пол­но­стью освещён, если на­строй­ки про­ек­то­ра оста­ют­ся не­из­мен­ны­ми?

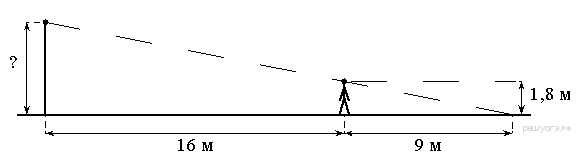
98. Че­ло­век, рост ко­то­ро­го равен 1,8 м, стоит на рас­сто­я­нии 16 м от улич­но­го фо­на­ря. При этом длина тени че­ло­ве­ка равна 9 м. Опре­де­ли­те вы­со­ту фо­на­ря (в мет­рах).

 

99. По­жар­ную лест­ни­цу при­ста­ви­ли к окну, рас­по­ло­жен­но­му на вы­со­те 12 м от земли. Ниж­ний конец лест­ни­цы от­сто­ит от стены на 5 м. Ка­ко­ва длина лест­ни­цы? Ответ дайте в мет­рах

 

.

100. Какой угол (в гра­ду­сах) об­ра­зу­ют ми­нут­ная и ча­со­вая стрел­ки, когда часы по­ка­зы­ва­ют ровно 4 часа?

 

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: