 |
Задание 4. Расчет параметров модели Земли
|
|
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(национальный исследовательский университет)»
Кафедра «Интегрированные бортовые комплексы навигации и наведения ЛА»
Специальность «Измерительно-вычислительные комплексы воздушно-космических ЛА»
Отчет о практической работе
по дисциплине: «Основы теории пилотажно-навигационных систем»
Выполнил: студент
группы СО-302С
Иванов И.И.
Преподаватель:
Ползик В.П.
г. Жуковский
2017г.
Задание 1. Расчет параметров ортодромии
1. Расчет длины и путевого угла ортодромии между двумя точками.
Даны географические координаты точек:
Город 1 j1 = l1 =
Город 2 j2 = l2 =
Вычислить значения:
· S – длина ортодромии в угловой мере (градус) и в линейной мере (км).
· β1 – путевой угол ортодромии в градусах.
Расчет выполнить в среде Excel и результаты представить в виде таблицы
| Ортодромия | j1 | l1 | j2 | l2 | cosS | Sгр | Sкм | ctgβ1 | β1 |
В отчет поместить исходные данные и формулы для расчета.
Формулы для расчета
1) Длина ортодромии S в угловой мере и в км:
cosS = sinφ1 sinφ2 + cosφ1 cosφ2 cos(l2-l1)
S = arcos(cosS) – в радианах
S* 57,3– в градусах
1° дуги = 111,2 км
S* 111,2– в км
2) Путевой угол β1 ортодромии, проходящей из первой точки (φ1, λ1) во вторую (φ2, λ2), и измеренный относительно меридиана первой точки определяется по формуле:
ctgβ1 = tgφ2 cosφ1 / sin(l2 – l1) – sinφ1 ctg(l2-l1)
β1 = arcctg(ctgβ1) – в радианах
β1 *57,3 – в градусах
Задание 2. Расчет параметров локсодромии
2. Расчет длины и путевого угла локсодромии между двумя точками.
|
|
|
Даны координаты точек:
· координаты точек (j1, l1) и (j2,l2) из первой задачи.
Вычислить значения:
· β – путевой угол локсодромии в градусах.
· S – длина локсодромии в угловой мере (градус) и в линейной мере (км).
Расчет выполнить в среде Excel и результаты представить в виде таблицы
| Локсодромия | j1 | l1 | j2 | l2 | jср | tgβ | β | Sгр | Sкм |
В отчет поместить исходные данные и формулы для расчета.
Формулы для расчета
φср = (φ2+φ1)/ 2средняя широта перелета.
β – локсодромический путевой угол
tgβ = (λ2 – λ1) / (φ2 − φ1) * cosφср
β = arctg(tgβ) – в радианах
β *57,3 – в градусах
Длина локсодромии S в угловой мере и в км
S = (λ2 − λ1) / sin β * cosφm в градусах
1° дуги = 111,2 км
S* 111,2– в км
Задание 3. Расчет гравитационного ускорения
3. Расчет ускорения свободного падения:
Даны:
· координаты точек (j1, l1) и (j2 l2) из первой задачи.
· высоты точек над уровнем моря H1 = H2 =
· высота эшелона Hэш =
Вычислить значения:
g01 – ускорения свободного падения в точке 1 у поверхности Земли.
g02 – ускорения свободного падения в точке 2 у поверхности Земли
g1эш – гравитационное ускорение в точке 1 на высоте эшелона.
g2эш – гравитационное ускорение в точке 2 на высоте эшелона.
Расчет выполнить в среде Excel и результаты представить в виде таблицы
| Координаты | j | l | H | Hэш | Rз | g0 | gэш |
| Точка 1 | |||||||
| Точка 2 |
В отчет поместить исходные данные и формулы для расчета.
Формулы для расчета
Значения ускорения свободного падения вычисляются по эмпирической формуле (в м/с²):
g = 9,780327 (1,0 + 0,0053024 sin2φ – 0,0000058 sin2(2φ) – 3,086 10-6 H.
где φ – широта места, H – высота точки над уровнем моря в метрах.
Гравитационное ускорение на высоте Hэш определяется по формуле

где: g0 – гравитационное ускорение на поверхности Земли.
gH – гравитационное ускорение на высоте Hэш.
|
|
|
Rз = 6371·км – радиус Земли
Задание 4. Расчет параметров модели Земли
4. Расчет радиуса кривизны в точке
Дано:
· эллипсоид Красовского: a = 6378245 м; b = 6356863 м
· эллипсоид WGS 84: a = 6378137 м; b = 6356752 м
· координаты точек (j1, l1) и (j2 l2) из первой задачи.
Вычислить
Для эллипсоида Красовского
e – первый эксцентриситет
e¢ – второй эксцентриситеты
f – полярное сжатие
N1 – радиус кривизны в точке 1
N2 – радиус кривизны в точке 2
Для эллипсоида WGS 84
e – первый эксцентриситет
e¢ – второй эксцентриситеты e¢
f – полярное сжатие
N1 – радиус кривизны в точке 1
N2 – радиус кривизны в точке 2
Расчет выполнить в среде Excel и результаты представить в виде таблицы
| Параметры | a | b | e | e¢ | f | j | l | N1 | N2 |
| эллипсоид Красовского | |||||||||
| эллипсоид WGS 84 |
В отчет поместить исходные данные и формулы для расчета.
Формулы для расчета
Первый и второй эксцентриситеты
 ,
, 
полярное сжатие
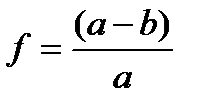
радиус кривизны первого вертикала

а – большая полуось (экваториальный радиус);
b – малая полуось (полярный радиус).
j – широта места.
|
|
|


