Главная | Обратная связь | Поможем написать вашу работу!

Порядок представления и защиты контрольной работы

Контрольная работа сдается на проверку в сроки, установленные планами-графиками. В результате рецензирования работы преподавателем студент получает одну из двух оценок: «допущен к собеседованию», «не допущен к собеседованию». В последнем случае необходимо после исправления отмеченных преподавателем недостатков представить работу для повторного рецензирования. Работы с оценкой «допущен к собеседованию» должны быть защищены на экзамене.

6. Очная учеба студентов.

Студенты, успешно выполняющие учебный план, приглашаются в университет для проведения лабораторных работ, сдачи экзаменов и очной работы с преподавателями. В это время для студентов читаются обзорные лекции и проводятся упражнения в объеме учебного плана.

Следует иметь в виду, что обзорные лекции не являются систематическим чтением курса. Они охватывают лишь узловые моменты программы. Обзорные лекции, упражнения и консультации будут полезны студентам, которые проработали курс по полной программе и выполнили контрольные задания.

Бюджет времени (в часах)

Таблица 3

Аудиторная работа	Самостоятельная работа
Лекции	Пр. занятия	Итого	Изучение курса	Выполнение контрольных работ	Итого

7. Сдача экзамена.

К сдаче экзамена допускаются студенты, имеющие на руках выполненные и зачтенные контрольные работы. Экзамены сдаются устно.

При сдаче экзаменов студент должен знать все определения, формулы, теоремы и их доказательства, а также уметь решать задачи по данному курсу.

РАБОЧАЯ ПРОГРАММА

1. Комплексные числа

1.1. Комплексные числа, их изображение на плоскости. Модуль и аргумент комплексного числа. Сопряженные комплексные числа. Формулы Эйлера.

1.2. Алгебраическая, тригонометрическая и показательная формы комплексного числа. Формула Муавра.

1.3. Операции над комплексными числами.

2. Неопределенный интеграл

2.1. Первообразная, неопределенный интеграл, его простейшие свойства. Таблица основных первообразных.

2.2. Непосредственное интегрирование функции. Интегрирование заменой переменной. Интегрирование по частям.

2.3. Интегрирование дробно-рациональных функций с помощью разложения на простейшие дроби.

2.4. Интегрирование функций, содержащих квадратный трехчлен. Интегрирование иррациональных функций.

2.5. Интегрирование тригонометрических функций. Тригонометрические подстановки. Интегрирование гиперболических функций.

3. Определенный интеграл „

3.1. Задачи, приводящие к понятию определенного интеграла. Интеграл от непрерывной функции как предел интегральных сумм. Теорема о существовании определенною интеграла. Свойства определенного интеграла.

3.2. Производная от определенного интеграла по переменному верхнему пределу. Формула Ньютона-Лейбница.

3.3. Вычисление определенного интеграла с помощью интегрирования по частям и заменой переменной.

3.4. Несобственные интегралы I и II рода. Основные свойства, признаки сходимости, абсолютная и условная сходимость несобственных интегралов.

3.5. Приложения определенных интегралов:

3.5.1. Вычисление площадей плоских фигур в декартовых и полярных координатах.

3.5.2. Вычисление длины дуги.

3.5.3. Вычисление объема тела и площади поверхности вращения.

3.5.4. Применение интеграла к решению физических задач.

4. Кратные интегралы

4.1. Задачи, приводящие к понятиям двойного, тройного интегралов. Кратный интеграл как предел интегральных сумм. Основные свойства интегралов. Среднее значение функции в области. Геометрический смысл двойного интеграла. Кратные интегралы произвольной размерности.

4.2. Замена переменных в кратных интегралах. Переход от декартовых координат к полярным, цилиндрическим, сферическим системам координат.

4.3. Вычисление кратных интегралов путем сведения их к повторным интегралам.

Приложения кратных интегралов. Вычисление объемов и площадей.

В результате изучения программы 2 семестра по курсу высшей математики студент должен;

1. Уметь найти модуль и аргумент комплексного числа, если оно задано в алгебраической форме.

2. Уметь перейти от алгебраической формы записи комплексного числа к тригонометрической и показательной и обратно.

3. Уметь выполнять алгебраические действия с комплексными числами; сложение, вычитание, умножение, деление, возведение в степень 11-извлечение корня.

4. Формулировать определение первообразной функции и неопределенного интеграла.

5. Знать и уметь использовать таблицу основных неопределенных интегралов.

6. Уметь пользоваться методом замены переменной при интегрировании.

7. Уметь использовать метод интегрирования по частям.

8. Уметь пользоваться справочником по высшей математике для отыскания первообразной функции и неопределенного интеграла.

9. Знать определение, геометрический и физический смысл определенного интеграла.

10. Уметь использовать формулу Ньютона-Лейбница для вычисления определенных интегралов, в том числе и в случае замены переменной и интегрирования по частям.

11. Знать и уметь использовать основные свойства определенного интеграла.

12. С помощью определенного интеграла уметь вычислить площадь плоской фигуры, ограниченной графиками известных функций.

13. Уметь вычислить с помощью определенного интеграла длину дуги кривой, объем и площадь поверхности тела вращения.

14. Уметь исследовать сходимость несобственного интеграла и вычислять его в случае, когда он существует (сходится).

15. Знать определение, геометрический смысл, основные свойства двойного интеграла и уметь применять их.

16. Уметь записать двойной интеграл в заданной области в виде двукратного интеграла и вычислить его.

17. С помощью двойного интеграла уметь вычислить площадь плоской фигуры и объем цилиндрического тела.

18. С помощью тройного интеграла уметь вычислить объем, массу тела и координаты центра масс, если известны поверхности, ограничивающие данный объем, и функция распределения плотности в объеме.

19. В двойном интеграле уметь перейти от декартовых координат к полярным в тех случаях, когда это упрощает его вычисление.

20. В тройном интеграле уметь совершать переход от декартовых координат к сферическим в тех случаях, когда это упрощает его вычисление.

Номер варианта для выполнения контрольной работы определяется следующим образом:

1. Если две последние цифры номера студенческого билета образуют число меньше 51, то это число и является номером варианта.

2. Если две последние цифры номера студенческого билета образуют число больше или равное 51, то для получения номера варианта из этого числа нужно отнять 50 (например, если номер студенческого билета ЗЭ801068, то номер варианта будет равен 68-50=18).

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РАЗДЕЛАМ КУРСА

РАЗДЕЛ I. КОМПЛЕКСНЫЕ ЧИСЛА

Вопросы, подлежащие изучению

1. Комплексные числа, их изображение на плоскости.

2. Алгебраические действия над комплексными числами. Модуль и аргумент комплексного числа.

3. Сопряженные комплексные числа, формулы Эйлера.

1. Рассмотрим различные формы записи комплексных чисел. Запись комплексного числа z в виде (1) называется алгебраической формой комплексного числа, при этом х и у – действительные числа, – мнимая единица, определяемая условием . Сопряженное комплексное число есть .

Комплексное число изображается как точка М на координатной плоскости х0у с координатами (х,у), либо как вектор, ищущий из начала координат, с проекциями {x,y} при этом (1) рассматривается как разложение вектора Z по осям координат (рис.1.). Проекция х и у называются действительной и мнимой частью комплексного числа Z и обозначаются Таким образом,

Наряду с представлением комплексного числа в форме (1) удобно пользоваться его представлением в полярных координатах. Если r и φ - полярные координаты точки , то . (2)

Выражние (2) называется триганометрической формой комплексного числа, при этом величина к назывется модулем комплексного числа z и равна 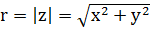, (3), а величина называется аргуметом комплексного числа и обозначается , при этом – главное значение аргумента такое, что .

При нахождении угла из последнего соотношение надо учитывать четверть, в которой находится угол .

Пример 1. Записать комплексное число z=-1+i в триганометрической форме.

Решение. Для заданного числа z=-1+i имеем

Тогда

Отсюда 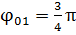или .

Очевидно, что угол лежит во второй четверти, так как точка z находится во второй четверти. Поэтому .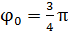

В итоге имеем .

Сопряженное комплексное число в триганометрической форме записывается так: , при этом , .

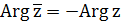При z=0 модуль |z|=0, а величина не определена.

Применяя формулу Эйлера , комплексное число можно записать в показательной форме: . (4)

Необходимо уметь переходить от показательной формы комплексного числа к тригонометрической и алгебраической формам и обратно. При рассмотрении разности двух комплексных чисел необходимо иметь в виду, что модуль этой разности имеет геометрический смысл окружности с центром в точке и радиусом ρ, так как по определению .

Но или .

Полученное алгебраическое выражение есть уравнение окружности радиуса в плоскости х0у с центром в точке . Неравенство описывает тогда множество точек, лежащих внутри указанной окружности и на самой окружности, а неравенство есть множество точек, лежащих вне указанной окружности.

Пример 2. На комплексной плоскости начертить область, удовлетворяющую условиям ;

Решение. Неравенство выделяет на плоскости кольцо с центром в точке 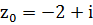с внутренним радиусом 1 и внешним радиусом 3, причем внутренняя окружность принадлежит заданной области, а внешняя - не принадлежит (рис. 2а).

Второе условие выделяет сектор с центром в точке 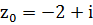с лучами и 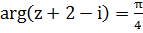, причём оба луча принадлежат области (рис.2б).

Третье условие выделяет из сектора кольца A,B,C,D ту его часть, для точек которой справедливо неравенство х<0.5,причем граница области не принадлежит (рис. 2в).

Четвертое условие выделяет из сектора кольца A,B,C,D ту его часть, для точек которой справедливо неравенство , причём граница принадлежит области (рис.2г).

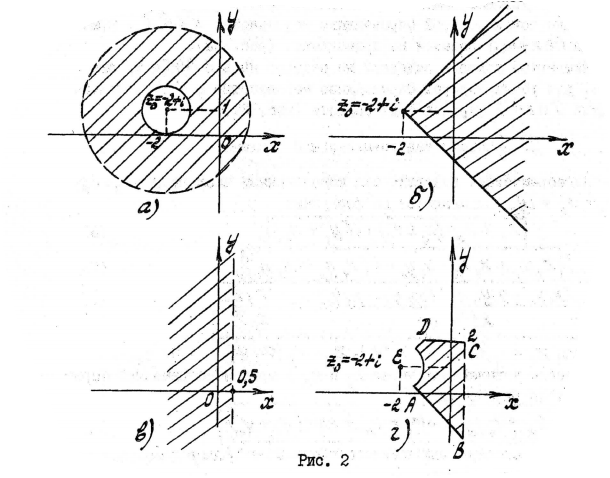
2. Действия на комплексными числами

Алгебраические дествия над комплексными числами и выполняются по формулам:

; (5)

; (6)

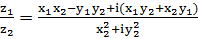; (7)

Если 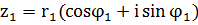, , то умножение комплексных чисел 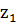и 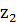в триганометрической форме определяется равенством (8)

Возведение в степень комплексного числа определяется равенством , (9)

При этом ; . (10)

Операция извлечения корня n-ой степени из комплексного числа определяет n различных комплексных значений по формуле (11)

Точки расположены в вершинах правильного многоугольника, вписанного в окружность с центром в начале координат и радиусом .

Пример 3. а) решить уравнение 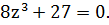Значение корней хаписать в триганометрической, алгебраической и показательной формах. Изобразить решение на комплексной плоскости.

б) вычислить сумме двух первых корней . Результат записать в показательной форме.

Решение. а) перепишем уравнение следующим образом .

Число запишем в триганометрической форме 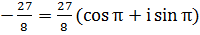, так как

Тогда по формуле (9), пологая 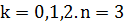, получим , откуда 1) ;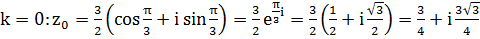

2) ;

3) .

Все три корня 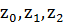расположены на окружности радиуса 3/2 и являются вершинами правильного треугольника (рис.3).

б) Вычислим сумму (). Сложение выполняем в алгебраической форме: .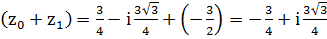

Чтобы записать результат в показательной форме, найдём модуль и аргумент полученной суммы:

Отсюда имеем ;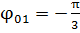

Из чертежа видно, что точка () лежит во второй четверти. Поэтому . В результате имеем .

Вопросы для самомпроверки.

1. Как геометрически представляют комплексные числа?

2. Что называется, действительной и мнимой частью комплексного числа?

3. Что называется модулем и аргументом комплексного числа?

4. Какова связь между алгебраической, показательной и тригонометрической формами комплексного числа?

5. Как умножаются и делятся комплексные числа в тригонометрической форме?

6. Как определяется n-я степень комплексного числа?

7. Напишите формулу для извлечения корня n -й степени из комплексного числа.

8. Напишите формулу Эйлера.

Раздел 2. Неопределённый интеграл.

Литература

Л.1.1. (гл.3 ст.145-171)

Л.1.2. (ст.96-115)

Л.1.3. (Демидович №1031-1500(выборочно))

Вопросы, подлежащие изучению

1. Неопределенный интеграл, первообразная, ее простейшие свойства. Таблица основных интегралов.

2. Непосредственное интегрирование функций, интегрирование по частям и подстановкой.

3. Интегрирование рациональных дробей, некоторых иррациональных функций.

4. Интегрирование рациональных дробей и иррациональных функций, содержащих квадратный трехчлен.

5. Интегрирование тригонометрических функций.

6. Интегрирование иррациональных функций с помощью тригонометрических подстановок.

7. Интегрирование гиперболических функций.

В предыдущем семестре мы в основном занимались следующей задачей: по данной функции F(x) надо было найти ее производную f(х) = F`(х). Изучив основные приемы дифференцирования, мы встретились с некоторыми важными приложениями понятия производной (нахождение экстремумов функций, уравнений касательных, скоростей и т.д.), узнали, что не все функции дифференцируемы (например, функция у = |x| в точке х = 0), что из дифференцируемости следует непрерывность.

Теперь мы переходим к следующему гораздо более сложное и не менее важному разделу высшей математики. - интегральному исчислению. Основная задача интегрирования прямо противоположна соответствующей задаче дифференциального исчисления: по данной производной f(х) некоторой неизвестной функции F (х) на данном интервале (а,в) найти саму эту функцию F(х) на этом интервале (мы, как правило, будем считать, что (а,в) = ).

2.1. Первообразная. Свойства неопределенного интеграла.

В этом случае функция F(х) называется первообразной от функции f(х). Совокупность всех первообразных функции -f(х)(их вообще говоря бесконечно много) называется неопределенным интегралом от функции f(х) и обозначается .

Нетрудно показать, однако, что любые две первообразные и 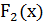данной функции f(x) отличаются лишь на константу,. т.е. 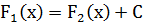. Верно и обратное: если 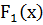- первообразная функции , то и 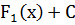- первообразная той же функции для любого числа С.

Таким образом, для нахождения неопределенного интеграла от данной функции f(х) достаточно найти лишь одну (любую!) первообразную F(х) от нее, а все остальные получаются сдвигом на константу, т.е.

Заметим сразу, что так как не всякая функция является производной некоторой функции, то и определен не для всякой функции. Однако если - непрерывна, то интеграл существует. Таким образом,

Этого свойства нам будет вполне достаточно в дальнейшем, так как мы будем находить только интегралы от непрерывных функций.

Перейдем теперь непосредственно к технике интегрирования, необходимой для выполнения контрольных работ и для дальнейшего изучения математики. Попутно мы будем кратко (все свойства без доказательств!) останавливаться на некоторых теоретических моментах и акцентировать внимание на важнейших практических приемах интегрирования. Для более полного ознакомления с предметом необходимо, разумеется, ознакомление с соответствующими разделами из литературы, указанной в начале этой теш (возможно использование и других источников).

Для того, чтобы научиться более или менее свободному владению техникой интегрирования, необходимо, в первую очередь выучить наизусть (!) таблицу простейших интегралов, которая приводится в любом пособии по высшей математике и является как бы "таблицей простейших производных - наоборот" (так как производная от правой части должна дать подынтегральное выражение в левой части). Поэтому запомнить их не очень сложно, хотя среди них встречаются четыре интеграла, которые запоминаются, как правило, не сразу. В силу этого мы приведём их отдельно (во второй рамке мы используем неравенство |a-x|=|x-a|):

, , , .

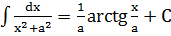Отметим теперь некоторые простейшие свойства неопределенного интеграла:

1. Неопределенный интеграл от дифференциала функции F(х) равен F(х) + С, где С пробегает все действительные числа, т.е.

2. Интеграл от суммы (соответственно разности) двух функций равен сумме (соответственно разности) их интегралов, т.е. .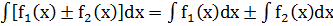

3. Постоянный множитель можно вносить за знак интеграла, т.е. .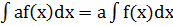

4. .

Пример 1. 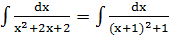, осталось воспользоваться свойством 4 и табличным интегралом .

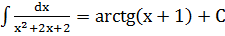Пример 2.

В предпоследнем равенстве мы воспользовались табличными интегралами 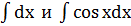, а также свойством 4.

Перед тем как перейти к изучению двух важнейших методов интегрирования - методу подстановки и методу интегрирования по частям - обязательно нужно вспомнить понятие дифференциала функции, умение применять которое необходимо в обоих методах.

Дифференциал функции φ(х) (обозначается dφ(x))есть произведение ее производной на дифференциал переменной x, или что то же на приращение переменной х (обозначается 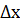, а чаще - ), т.е.

Весьма полезно знать некоторые наиболее чаото встречающиеся в интегрировании выражения, являющиеся дифференциалами: и др.

2.2. Метод подстановки

Пожалуй, самым часто иопользуемым приемом при интегрировании является метод подстановки (или замены переменной) в неопределенном интеграле:

Этот метод позволяет сводить довольно сложные интегралы (содержащие, как правило, в подынтегральном выражении дифференциал какой-нибудь функции, которую и выбирают за новую переменную, в явном виде) к табличным или уже известным.

Очень важно еще отметить следующее: так как возможны различные методы вычисления одного и того же интеграла, то в итоге могут получиться совершенно непохожие на вид ответы; поэтому лучшей проверкой ответа является его дифференцирование - результат должен совпасть с подынтегральной функцией.

Пример 3.

. Замена

Если вы использовали метод подстановки, не забывайте в ответе вернуться к старой переменной!

Пример 4. .

Разумеется, в этом примере былобы неразумно и заняло бы слишком много времени возводить (2х -3) в 21 степень (хотя такие случаи и встречались). Всегда надо стремиться делать замену, которая упрощает подынтегральное выражение. Здесь очевидна подстановка 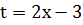. Тогда , откуда окончательно: .

Пример 5.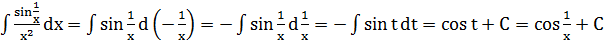

Пример 6. Пусть многочлен не емеет действительных корней. Тогда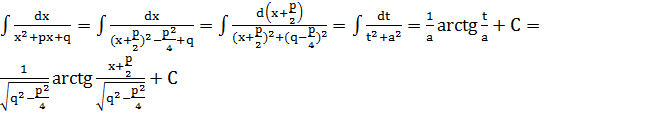

2.3. Метод интегрирования по частям

Вторым важнейшим приемом интегрирования является метод интегрирования по частям (u(х) и v(х) - дифференцируемые функции):

Это правило применяется обычно, когда подынтегральное выражение можно представить в виде и , причем выражение существенно проще, чем u, а выражение v несущественно сложнее . В результате получается проще исходного интеграла . С помощью этого метода считаются многие интегралы, например, интегралй от обратных тригонометрических функций , интегралы вида

В некоторых случаях (как при вычислении интеграла ) это правило интегрирования по частям применяется дважды; часто в промежуточных вычислениях используется еде и метод подстановки. Таким образом, мы убеждаемся в том, что интегрирование является гораздо более сложным математическим искусством, требующим определенных навыков, а порой и изобретательности.

Пример 7. .

Положим jnrelf В качестве v возьмём простейшёю первообразную в семействе , т.е. (мы воспользовались тем, что ).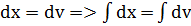

Тогда по правилу интегрирования по частям

Этот интеграл весьма часто используется в контрольных заданиях.

Пример 8.

Пример 9.

, снова интегрируем по частям: , откуда

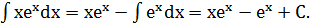
Окончательно: .

2.4. Интегрирование рациональных функций.

Большую роль в теории интегрирования играет понятие рациональной функции.

Рациональная функция одной переменной может быть представ» лена в виде:

, где Q и Р - многочлены. Если степень многочлена Q меньше степени многочлена Р, такая рациональная функция (рациональная дробь) называется правильной. Если степень многочлена Q больше или равна степени многочлена Р, дробь называется неправильной.

Например, рациональными являются функции:

причем , является правильной рациональной дробью, a 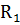и неправильными рациональными дробями.

Рациональная функция нескольких аргументов может быть представленна в виде , где Q и P – многочлены с переменными .

Например, рациональными функциями двух переменных являются:

, , .

Функция R может быть пациональной с переменными

Например, если , то рациональными будут следующие функции(в скобках указаны соответсвующие переменные):

, .

В то же время функции и 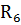не являются рациональными функциями аргумента x; функция не является рациональной функцией ни от X, ни от sinx, ни от cosx в отдельности.

Для нахождения интегралов вида 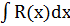применяют разложение подынтегральной функции на простейшие дроби. При этом если дробь R(х) неправильная, то предварительно выделяют в R(х) целую часть делением одного многочлена на другой.

Пример 10. Найти .

Под знаком интеграла стоит дробно-рациональная функция .

Так как эта дробь правильная, то ее можно представить в виде суммы простейших дробей следующим образом: .

После приведения к общему знаменателю получим следующее представление: ,

где А, В, С - некоторые постоянные, которые надо определить. Последнее равенство верно при всех значениях х. Ввиду равенства знаменателей следует равенство числителей: или

Тождественное равенство многочленов означает, что коэффициенты при одинаковых степенях х у этих многочленов совпадают, т.е.

- коэффициенты при

Из этой системы уравнений находим: А = -4, В = -7, С =5.

Те же значения постоянных А, В, С можно получить и из следующих соображений. Тождественное равенство двух функций означает, что они совпадают при любых значениях х. Подставляя в тождество многочленов х-1, получим - 48 = -12А т.е. А = 4; подставляя х = -3, получим -196 = 28В, т.е. В = -7; подставляя х = 4, получим 105 = 21С, т.е. С = 5.

Таким образом, получено разложение подынтегральной функции на простейшие дроби: .

Тогда .

Пример 11. Найти .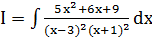

Подынтегральная функция представляет собой правильную рациональную дробь. Разложим ее на простейшие дроби , или .

Из равенства дробей, равенства их знаменателей следует, что равны их числители: или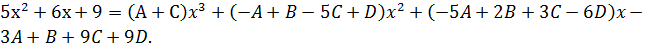

Эти многочлены тождественно совпадают, следовательно, равны коэффициенты при одинаковых степенях х, т.е.

- при

Решая систему этих уравнений, находим A=0, Таким образом,

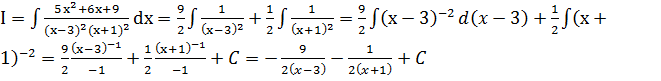Пример 12. Найти

Степень многочлена, стоящего в числителе подынтегральной дроби, равна степени многочлена, стоящего в ее знаменателе, т.е. дробь неправильная, поэтому перед разложением дроби на простейшие надо выделить в ней целую часть. В общем случае это делают делением многочленов, но в данном случае проще выделить в числителе многочлен, стоящий в знаменателе, прибавив и отняв в числителе X, т.е.

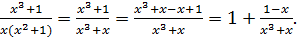
Разложим на простейшие дробь :

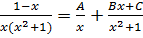или

Из простейшего равенства получаем тожество или .

Приравняем коэффициенты при равных степеняx x:

- коэффициенты при

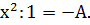
Откуда имеем: 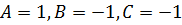. Тогда .

При нахождении I мы воспользовались тем, что

2.5. Интегрирование некоторых классов тригонометрических функций

Основным методом нахождения интегралов от тригонометрических функций является метод подстановки. В некоторых случаях метод подстановки применяется после предварительного преобразования подынтегральной функции с помощью известных из тригонометрии формул.

1. Интегралы вида 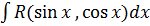с помощью универсальной тригонометрической подстановки сводятся к интегралу от рациональной функции аргумента t.

В некоторых частных случаях проще применять другие подстановки, кроме универсальной.

1. Для вычисления интеграла вида применяют подстановку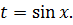

2. Для вычисления интеграла вида применяют подстановку

3. Для вычисления интеграла вида 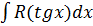применяют подстановку

4. Если 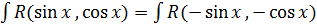, т.е. если при одновременном изменении знака y и