 |
Задача 5.2. Измерить с помощью транспортира прямые и обратные дирекционные углы линий АВ, ВС, СА. Вычислить значения их румбов и внутренних углов треугольника.
|
|
|
|
Так как дирекционный угол – это угол между северным направлением осевого меридиана и направлением заданной линии, измеренный по ходу часовой стрелки, то решение первой части задачи сводится к измерению угла между вертикальной линией сетки (осью абсцисс) и заданной линией. Результаты измерений записывают в таблицу №6. В качестве примера в ней переведены результаты измерений дирекционных углов сторон треугольника АВС приложения 1.
Прямой и обратный дирекционные углы отличаются ровно на 180°. Учитывая погрешность измерения результаты могут отличаться на 180 °±1°30'.
Рис. 16. Измерение дирекционных углов на карте
Таблица 6. Результаты измерения дирекционных углов сторон треугольника АВС
| Название линий | Дирекционные углы, α | Румбы, r | Углы |
| АВ | 262°00´ | юз:82°00´ | ÐА=56°00´ |
| ВС | 23°00´ | св:23°00´ | ÐВ=59°30´ |
| СА | 137°30´ | юв:42°30´ | ÐС=66°00´ |
| ВА | 82°30´ | св:82°30´ | |
| СВ | 203°30´ | юз:23°30´ | |
| АС | 318°00´ | сз:42°00´ | ∑=181°30´ |
Задача 5.3. Вычислить дирекционные углы сторон АВ,ВС,СА по формуле 13, используя прямоугольные координаты, полученные в задаче 3.1 и сравнить их с измеренными (табл. 7). Дать анализ причин расхождений между вычисленными измеренными дирекционными углами.
Дирекционный румб линии можно вычислить, зная прямоугольные координаты концов отрезка АВ (ХA,YA,XB,YB), по формуле:
(13)
Для перехода от румба к дирекционному углу необходимо установить направление четверти, в которой он находится, ориентируясь на знаки приращений координат (YВ-YА) и (XВ-XА) в соответствии с табл.7, а затем вычислить искомый дирекционный угол по табл.6 или рис. 14.
Таблица 7. Знаки приращений координат в зависимости от четверти
|
|
|
| Разность координат | СВ | ЮВ | ЮЗ | СЗ |
| YВ-YА | + | + | - | - |
| XВ-XА | + | - | - | + |
Для примера рассмотрим линию АВ:
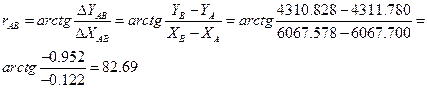Значения минут нужно перевести из сотых долей для этого 69 нужно умножить на 0,6. Согласно таблице №7 направление румба СЗ:82°41'.
Таблица 8. Результаты сравнения вычисленных и измеренных дирекционных углов
| Линия | Вычисленные румбы, r | Вычисленные дирекционные углы, α выч | Измеренные дирекционные углы, α изм | ∆=α выч- α изм |
| АВ | юз: 82°41´ | 262°41´ | 262°00´ | 0°41´ |
| ВС | св: 22°28´ | 22°28´ | 23°00´ | - 0°32´ |
| СА | юв: 41°45´ | 138°15´ | 137°30´ | 0°45´ |
| ВА | св: 82°41´ | 82°41´ | 82°30´ | 0°11´ |
| СВ | юз: 22°28´ | 202°28´ | 203°30´ | -1°02´ |
| АС | сз:41°45´ | 318°15´ | 318°00´ | 0°15´ |
Задача 5.4. Найти сближение меридианов как разность между истинным азимутом (табл. 5) и дирекционным углом (табл. 6) для точек А, В, С.
Таблица 9. Вычисление сближений меридианов
| Название сторон | Истинные азимуты Аизм | Дирекционные углы, α изм | Сближение меридианов γвыч |
| АВ | 260°00´ | 262°00´ | -2°00´ |
| ВС | 21°30´ | 23°00´ | -1°30´ |
| СА | 135°30´ | 137°30´ | -2°00´ |
Задача 5.5. Вычислить магнитные азимуты линий АВ, ВС, СА, используя значения дирекционных углов (табл. 6), а склонение магнитной стрелки и сближение меридианов взять из приложения 2 по заданному преподавателем варианту. Решение задачи иллюстрировать рисунками.
В табл. 10 приведены результаты вычисления магнитных азимутов сторон треугольника при γ=-2°15´, δ=4°20´.
.
Таблица 10. Вычисление магнитных азимутов
| Название линий | Дирекционные углы, α | Сближение меридианов, γ | Склонение магнитной стрелки, δ | Магнитный азимут, Ам |
| АВ | 262°00´ | -2°15´ | 4°20´ | 255°25´ |
| ВС | 23°00´ | -2°15´ | 4°20´ | 16°25´ |
| СА | 137°30´ | -2°15´ | 4°20´ | 130°55´ |
Вопросы для самоконтроля
1. Что называется истинным меридианом, параллелью, осевым меридианом?
|
|
|
2. Что означает ориентировать линию?
3. Что называется истинным азимутом, дирекционным углом, магнитным азимутом, румбом линии?
4. Какова зависимость между прямым и обратным азимутом?
5. В чем отличие сближения меридианов в проекции Гаусса-Крюгера от сближения меридианов в общем случае?
6. Что называется склонением магнитной стрелки?
7. Почему ориентирование по магнитному меридиану применяется сравнительно редко?
8. Как вычислить магнитный азимут, если известен географический азимут?
9. Как вычислить магнитный азимут, если известен дирекционный угол?
6. Рельеф и его изображение на картах и планах
Совокупность неровностей земной поверхности называют рельефом. На топографических картах и планах рельеф изображают горизонталями.
Горизонталь – это линия, соединяющая точки земной поверхности с одинаковыми высотами [[6]]. Понятие о горизонтали можно получить, если представить себе местность, затопленную до заданной высоты непроточной водой. Береговая линия в этом случае и будет являться горизонталью. Изменяя уровень воды (высоту уровневой поверхности), получим горизонтали с различными высотами. Чтобы правильно читать рельеф необходимо знать его основные формы.
 |
Рис. 17. Изображение форм рельефа на карте
На картах и планах высоты горизонталей изменяются через равные промежутки. Разность высот соседних горизонталей называют высотой сечения рельефа, а расстояние между горизонталями на плане – заложением.
Высоту сечения рельефа выбирают в зависимости от масштаба карты или плана и характера местности. Стандартные высоты сечения рельефа: 0,25; 0,5;1.0; 2.0; 2.5; 5.0; 10.0м. Горизонтали подписывают на планах и картах в разрывах основанием в сторону понижения ската местности. Кроме отметок горизонталей на картах подписывают отметки характерных точек рельефа (вершины горы, дна котловины и т. д.).
Основной характеристикой рельефа является крутизна ската. О ней можно судить по величине заложения. Заложение это расстояние между горизонталями на карте по заданной линии. Чем меньше заложение, тем круче скат и наоборот.
Для численной характеристики крутизны ската на местности используют угол наклона ν ° или уклон ί. Уклоном линии местности называют отношение превышения к горизонтальному проложению 
.
|
|
|
Уклон выражают в процентах или в промилях, а угол наклона в градусах.
При чтении рельефа руководствуются следующими правилами:
1) берг-штрихи направлены в сторону понижения;
2) основания цифр, которыми подписаны горизонтали, располагаются в направлении понижения ската;
3) к водоемам и водотокам местность понижается;
4) в одну сторону от горизонтали местность повышается, а в другую понижается;
5) горизонтали перегибаются на водораздельных линиях хребтов и тальвегах лощин;
6) отметка точки на горизонтали равна отметке горизонтали;
7) отметки горизонталей всегда кратны высоте сечения рельефа.
Для определения отметки горизонтали находят ближайшую подписанную горизонталь. Отметка искомой будет равна (рис. 18):
(14)
где Н0 – отметка подписанной горизонтали (145м);
n - число горизонталей между подписанной и искомой горизонталью
h0 - высота сечения рельефа.
 |
В формуле знак (+) ставится в случае, если точка А находится выше по склону подписанной горизонтали, а (-) - если ниже. На рис. 18 требуется определить отметку утолщенной горизонтали при h0=2,5м, n=2. Следовательно, отметка утолщенной горизонтали Н=145+2*2,5=150,0м.
Рис. 18. Определение высоты точки линейным интерполированием
Если определяемая точка находится между горизонталями, то сначала необходимо определить отметки горизонталей, между которыми они находятся (на рис. 18 отметки горизонталей 150м и 152,5м), а затем, превышение между горизонталью и определяемой точкой линейным интерполированием
(15),
где h1 - превышение между младшей горизонталью с отметкой Н 0 и точкой С;
в - заложение измеренное в мм на карте
a - расстояние от наименьшей горизонтали до точки С измеренное в мм.
Тогда отметка искомой точки будет равна:
(16)
Если определяемая точка лежит между горизонталями с одинаковыми отметками: перевал седловины, вершины горы или дно котловины, то отметка в этих случаях принимается равной отметке ближайшей горизонтали плюс (минус) половина высоты сечения рельефа.
|
|
|
Задача 6.1. Построить масштабы заложений для значений ν° и ί, приведенных в таблице №12.
Графики масштабов заложений показывают зависимость между крутизной ската и величиной заложения при данной высоте сечения. Так как крутизна ската может быть выражена в градусной мере или процентах, то в соответствии с этими имеется два вида графиков, - для углов наклона и уклонов.
Если крутизна ската выражена в градусной мере, то величину заложения a вычисляют по формуле:
(17)
а для крутизны ската, выраженной в процентах:
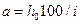(18)
где h0 - высота сечения рельефа на карте, выданной для выполнения работы.
Для построения графиков необходимо вычислить заложения a при ν и i,
приведенных в таблице 11.
Таблица 11. Исходные данные для построения графиков заложений
| Углы наклона, ν (°) | 0,5° | 1° | 2° | 3° | 4° | 5° | 7° | 10° | 20° |
| Заложения, а (м) | |||||||||
| Уклоны, i (%) | |||||||||
| Заложения, а (м) |
 |
При построении графиков обычно по горизонтальной линии откладывают равные отрезки произвольной длины, в концах которых восстанавливают перпендикуляры, и откладывают на них в масштабе своей карты соответствующее значение из табл.11. Концы перпендикуляров соединяют плавной линией (рис.19).
Рис. 19. Графики заложений
|
|
|
