Кусочно-линейные агрегаты

Как показывает анализ моделирующих алгоритмов, можно добиться их су­щес­твенных упрощений, если рассматривать объекты более частные, чем агрегат общего вида, но сохраняющие возможность описания достаточно широкого класса реальных систем. Пра­ктически удобным для формализации широкой сово­куп­но­сти разнообразных процессов и явлений материального мира являются так называемые кусочно-линейные агрегаты (КЛА).

Понятие о кусочно-линейном агрегате. Для поставленных здесь задач достаточно считать, что на агрегат не посту­па­ют управляющие сигналы z, а поступают лишь входные сигналы u (это допущение не огра­ни­чивает общности, так как в качестве u можно рассматривать входной сигнал в ши­ро­ком смысле, в том числе и управляющий). Итак, мы рассматриваем агрегат как объект, который в каж­дый момент времени t характеризуется внутренним состоянием x(t), имеет вход и выход. На вход агрегат в изолированные моменты времени могут пос­ту­пать сигналы, с выхода могут сниматься выходные сигналы. Класс кусоч­но-линейных агрегатов выделяется с помощью конкретизации структуры множеств X, U, Y а также операторов H и G, которые представляют собой линейные пространства. Опишем данную конкретизацию.

Рассмотрим некоторое конечное или счетное множество I. Для определенности предположим, что I = {0,1,2,…}, хотя в конкретных задачах I может иметь и другой вид. Назовем I множеством особых состояний, а элементы nÎI – особыми состояниями. Каждому особому состоянию nÎI поставим в соответствие некоторое целое неотрицательное число ||n||, которое назовем рангом основного состояния (смысл этой величины – размерность вектора n -го состояния). Кроме того, каждому nÎI поставим в соответствие выпуклый многогранник X⁽ⁿ⁾ (множество допустимых значений для состояния n) в евклидовом пространстве размерности ||n||. Будем считать, что X = ÈX⁽ⁿ⁾, т. е. пространство состояний X можно представить состоящим из всевозможных пар вида (), где nÎI, а x⁽ⁿ⁾ является вектором размерности ||n|| и принимает значения из многогранника X⁽ⁿ⁾. Вектор x⁽ⁿ⁾ будем называть вектором координат. Если ||n|| = 0 для некоторого n, то это означает, что в данном состоянии n координаты не определяются.

Процесс функционирования КЛА. Опишем сначала динамику КЛА, т.е. процесс изменения внутренних состояний во времени, в предположении отсутствия поступления u. В предыдущей терминологии, определим действия оператора Q. Пусть в начальный момент времени t₀ агрегат находится в состоянии x(t₀)=(n,x⁽ⁿ⁾(0)), где x⁽ⁿ⁾(0) - внутренняя точка многогранника X⁽ⁿ⁾. Тогда при t>t₀ точка x⁽ⁿ⁾(t) перемещается внутри многогранника X⁽ⁿ⁾ до тех пор, пока не достигнет его границы. Пусть это произойдет в момент t₁, который назовем «особым». Тогда при t₀<t£t₁ «движение» агрегата описывается следующими законами:

n(t)=n=const (2.10),

x⁽ⁿ⁾(t)=x⁽ⁿ⁾(0)+ (t-t₀)×a⁽ⁿ⁾. (2.11)

Данному значению n соответствует вектор a⁽ⁿ⁾ (скорость изменения координат) размерности ||n|| (cp. (2.7)).

Значение особого момента t₁ определяется траекторией x(t), вернее её некоторыми параметрами и может быть найдено из соотношения

t₁= inf {t: x⁽ⁿ⁾(0)+(t-t₀)a⁽ⁿ⁾ÏX⁽ⁿ⁾, t>t₀}. (2.12)

Поскольку X⁽ⁿ⁾ – многогранник, то нахождение t₁ по правилу (2.12) сводится к следующему. Предположим, что X⁽ⁿ⁾ содержит m граней. Эти грани могут быть заданы линейными уравнениями:

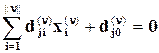, j = 1,…,m,

где x_i⁽ⁿ⁾ – компоненты вектора x⁽ⁿ⁾, i=1.. ||n||. Легко понять, что (2.12) может быть записано в виде

(2.13)

Обозначим 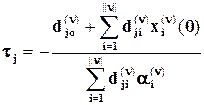, j=1,…m (2.14)

Пусть t=min{t_j;t_j>0} (2.15)

Тогда из (2.13)-(2.15) следует, что t₁=t₀+t

То есть t – это время, за которое агрегат может достичь ближайшей грани многогранника и прийти к смене состояния, а t₁ – ближайший особый момент времени.

В момент t₁ состояние рассматриваемого кусочно-линейного агрегата изме­ня­ется скачкообразно. Значение x(t₁+0) является, вообще говоря, случайным. В момент t₁ может выдаваться выходной сигнал y (см. оператор G). Содер­жание (и необходимость выдачи) y зависит от состояния x(t₁). Подмножество X_y, введенное в общем определении агрегата, в данном случае совпадает с . Важно указать, что множество Y имеет структуру, аналогичную X, т.е. выходные сигналы y представляются как y=(l, y ^(l)), где l – элемент некоторого счетного множества, y^(l) – вектор, принимающий значения из евклидова пространства размерностью, зависящей от l. При t>t₁ движение агрегата вновь происходит в соответствии с формулами (2.10) и (2.11) до очередного особого момента t₂, где вместо t₀ теперь нужно понимать t₁ и т.д.

Обратимся теперь к случаю поступления входного сигнала. Подчеркнем, что для КЛА множество U структурно аналогично множествам X и Y, т.е. u=(m, u^(m)), где m – элемент конечного или счетного множества, а u^(m) – вектор, размерность которого зависит от m. Следующее описание поведения КЛА можно рассматривать как раскрытие действия оператора V^’.

Пусть в рассматриваемый момент t состояние агрегата x(t)=(n, x⁽ⁿ⁾) и пусть в этот момент поступает входной сигнал u=(m, u^(m)). При этом состояние агрегата меняется скачкообразно. Значение x(t+0) является случайным, задаваемым распределением, которое, вообще говоря, зависит от x(t) и u. Будем считать, что в рассматриваемый момент может выдаваться выходной сигнал, содержание и необходимость выдачи которого зависит не только от состояния x(t) (и, быть может, x(t+0)), но и от содержания поступившего входного сигнала u. После рассматриваемого момента времени t движение агрегата происходит в соответствии с формулами (2.10) и (2.11) до следующего момента поступления входного сигнала или выхода вектора состояния на границу допустимых значений.

В виде КЛА могут быть формализованы многие реальные процессы: процессы передачи и обмена данными в сетях связи, системы массового обслуживания и материально-технического снаб­же­­­ния, процессы автомо­биль­ного движения на дорогах, разнообразные дис­к­рет­ные производ­ст­венные процессы, вычислительные системы и т.д. При этом всюду основные состояния агрегата указывают на качественно различ­ные состояния модели­руемых объектов. Дополнительные же координаты ха­ра­к­теризуют происхо­дящие количественные изменения и часто носят сугубо вспомогательный характер, «вбирая» в себя необходимую инфор­ма­цию о пре­дыстории модели. Следует отметить, что представление реальных систем в форме КЛА неоднозначно, поскольку неоднозначно могут быть выбраны сос­тояния агрегатов. Выбор же состояний определяется как целями иссле­дования, так и стремлением уменьшить размерность задачи. При этом всегда приходится идти на компромисс между точностью описания и полнотой получаемой информации с одной стороны и простотой модели – с другой.

Пример 1. Вероятностный автомат Мура. Этот автомат не имеет «жесткой» тактности, а изменяет свое состояние всякий раз, когда поступает входной сигнал. Пусть X – конечное множество внутренних состояний автомата, U – его входной (конечный) алфавит, Y – его выходной (конечный) алфавит. Для определенности будем считать, что

X={1,2,…N}, U={1,2,..K}, Y={1,2,..M}.

Динамика автомата описывается следующим образом. Если в момент t состояние автомата x(t)=i и поступил входной сигнал, u(t)=k, то состояние x(t+0)=j выбирается случайно с вероятностью , ³0, при любом k, 1£k£K. Выходной сигнал yÎY, выдаваемый в этот момент, является однозначной функцией «нового» состояния j: y=m=Ф(j), где Ф - некоторая детерминированная функция с областью определения X и множеством значений Y. Представим этот автомат в виде кусочно-линейного агрегата.

Состояние агрегата x(t) Î Х, не имеет дополнительных координат и определяется только его номером n. Следовательно, ||n|| = 0 при всех nÎХ. При таком выборе состояния КЛА не определяются многогранники X⁽ⁿ⁾, отпадают вопросы о движении внутри многогранника, выходе агрегата на границу.

Все движение рассматриваемого КЛА состоит из скачков состояния при по­с­ту­плении входных сигналов, причем ввиду отсутствия вектора координат речь идет лишь о скачках основного состояния n. Ecли в момент времени t* со­стояние агрегата было x(t*) = i и поступил входной сигнал u = k, то в сле­дующий момент времени состояние изменилось: x(t*+0)=j с вероятностью .

Т.о., требуется задать лишь распределение . Содержа­ние же выходного сигнала, выдаваемого в момент поступления входного, определяется только функцией Ф: y(t*+0)=Ф(j). Вообще, если предположить, что ||n||=0, ||l||=0, ||m||=0 " n, a, m, то легко видеть, что КЛА превращается в вероятностный автомат весьма общего вида.

Пример 2. Система массового обслуживания. Пусть на обслуживающий прибор поступает ординарный поток требований, причем i -е требование характеризуется параметром q _i, который представляет собой предельно допустимое время ожидания i -м требованием начала обслуживания. Заявки, для которых реальное время ожидания превышает допустимое q_i, получают отказ. Время обслуживания i -того требования равно z_i, причем {z_i} – последовательность независимых одинаково распределенных случайных величин. Искомыми являются вероят­ностные характеристики длины очереди и времени ожидания.

Представим данный процесс в виде КЛА. За состояние агрегата выберем вектор x=(n, x⁽ⁿ⁾), где n - число требований, находящихся в системе в текущий момент времени, ||n|| = n, а x⁽ⁿ⁾ – вектор, координаты которого определяются только при n>0 и имеют следующий смысл: x₁⁽ⁿ⁾ – время, оставшееся до окончания обслуживания требования, находящегося на приборе, а x_i⁽ⁿ⁾ (1<i£n) – длительности обслуживания требований, которые стоят в очереди и будут впоследствии обслужены. В соответствие с этим вектор a^{(n )} скоростей изменения дополнительных координат имеет компоненты a₁⁽ⁿ⁾=-1, a_i⁽ⁿ⁾=0 (1<i£n), многогранник X⁽ⁿ⁾ при каждом n>0 совпадает с первым октантом евклидова пространства размерности n: X⁽ⁿ⁾={x⁽ⁿ⁾: x_i⁽ⁿ⁾³0, i=1,2,.. n}

В качестве входного сигнала рассмотрим пару (1,q), где символ 1 просто указывает на факт поступления требования (и, таким образом, дискретная компонента m принимает лишь одно значение 1), а величина q равна допустимому времени ожидания поступающего требования (т.е. ||m||=1).

Рассмотрим динамику данного агрегата (рис.2.5). Между особыми моментами времени гладко изменяется лишь первая компонента вектора координат, остальные – неизменны. x ₁(t) = x ₁(t₀) – (t-t₀) (см. формулу (2.11), отсюда a₁⁽ⁿ⁾=-1). На рис. 2.5 – это движение от точки t до t*.

Пусть момент t* является моментом окончания обслуживания. Тогда с необходимостью x ₁(t*) = 0, t* = x ₁(t₀) +t₀ (на рис. 2.5 – точка t*), а
x(t*) = (n, 0, x₂⁽ⁿ⁾,..x_n⁽ⁿ⁾), где n>0.

Обслуженное требование должно покинуть систему, а его место занимает требование стоящее первым в очереди (если очередь не пуста). Следователь­но, из состояния x(t*) агрегат скачкообразно перейдет в состояние x(t*+0) = (n-1, x₂⁽ⁿ⁾,..x_n⁽ⁿ⁾), (на рис.2.5 – точка t*+0). При этом размерность вектора х уменьшилась на 1, а компонента x₂⁽ⁿ⁾ заняла место компоненты x₁⁽ⁿ⁾. Будем считать, что в рассматриваемый момент t* вы­ходной сигнал не выдается. Далее происходит обслуживание очередной заявки, что выражается в непрерывном уменьшении компо­ненты x₁⁽ⁿ⁾, а на рис. 2.5 отображается движением от точки t*+0 до точки t**.

Рассмотрим теперь случай поступления входного сигнала (1,q) в момент t^**. Пусть при этом состояние агрегата было x(t^**)=(n, x ⁽ⁿ⁾), где n³0. По­­ступление рассматриваемого входного сигнала означает приход в систему обслужи­ва­ния требо­ва­ния, обладаю­ще­го временем обслуживания z ипредельным временем ожидания q. (на рис. 2.5 – скачок агрегата из точки t** в точку t**+0). Рассмот­рим два случая: n=0 и n>0. В первом из них требование поступает в пустую систему, а во втором – в занятую обслуживанием. При n=0 состо­яние x(t^**+0) должно отражать тот факт, что поступившее требование сразу принято к обслуживанию и ему случайным образом назначено время обслу­живания, т.е. n=0, x(t^**)=(0), x(t^**+0)=(1,z), где z - случайная величина, имеющая заданное распределение. При n>0 состояние x(t^**+0) должно отражать тот факт, что требование будет принято к обслуживанию тогда и только тогда, когда его предельное время ожидания q превосходит реальное (т.е. q> ) и в случае, если оно принято, ему назначается случайное время обслуживания.

n>0

x(t^**)= (n, x ₁(t**),…, x _n(t**))

x(t^**+0)= (19)

 

Будем считать, что в момент t ^** выдается входной сигнал, фиксирующий имею­щуюся длину очереди, время ожидания и факт принятия или непринятия поступающего требования. В соответствии с этим предположим, что y=(l, y), где l=(l₁,l₂), l₁ – число требований, находящихся в системе в момент t^**, l₂=0 или 1, если поступающее требование не принимается или принимается соответственно к обслуживанию, ||l||=l₂, а компонента y равна времени ожидания принятым требованиям начала обслуживания.

В данном случае l представляет собой вектор размерности 2 с целочис­лен­ными компонентами. Из сказанного следует, что имеют место зависимости:

l₁=n

l₂ =

 

 

y = (координата определяется лишь при l₂=1)

Выходной сигнал накапливается в системе сбора статистики. l₁ используется для вычисления средней длины очереди, у – для вычисления среднего времени ожидания обслуживания.

Марковские цепи

Функционирование многих объектов представляет собой последова­тель­ность переходов их из одного состояния в другое (ЭВМ, каналы передачи информации…).

Система называется системой с дискретными состояниями, если мно­жество ее состояний конечно, а переходы из одного состояния в другое осуществляются скачком.

Последовательность состояний такой системы называется цепью.

Простейшей характеристикой случайного процесса, являющегося цепью, служит набор вероятностей состояний p₁(t), p₂(t),…, p_n(t), где p_i(t) – вероятность того, что в момент t система находится в состоянии i. p₁(t)+p₂(t)+…+ p_n(t)=1

Случайный процесс, протекающий в системе, называется марковским, если для любого момента времени t₀ вероятность любого состояния сис­темы в будущем (при t > t₀) зависит только от ее состояния в настоящем (при t = t₀) и не зависит от того, каким образом система пришла в это состояние.

Марков (старший) Андрей Андреевич (1856-1922) – русский математик, доктор физико-математических наук, профессор, академик Петербургской академии наук. Работал профессором Петербургского университета, опубликовал около 70 работ по теории чисел, теории приближенных функций, дифференциальных уравнений, теории вероятностей. В цикле работ, опубликованных в 1906-1912 годах, заложил основы одной из общих схем естественных процессов, которая была названа цепями Маркова. А.А. Марков пользовался большим авторитетом у студентов. Был материалистом и убежденным атеистом.

Переход системы из одного состояния в другое является в общем случае случайным событием. Последовательность смены состояний является потоком событий.

Поток событий является ординарным, если события происходят поодиночке (нет двух одновременных событий). Поток называется стационарным, если его вероятностные характеристики не изменяются во времени. Чаще всего применяются пуассоновские потоки событий, то есть имеющие неизменную интенсивность (плотность) – среднее число событий в единицу времени постоянна. l = const.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: